ZADANIA Z FIZYKI DLA STUDENTÓW WYDZIAŁU GiG
GiG SEM. I, 2012/2013,
ZESTAW 1
Zadania do rozwiązania w sekcjach:
1. Wyznaczyć wektory ![]()
oraz ![]()
, które można otrzymać z podanych wektorów ![]()
:
![]()
![]()
, ![]()
![]()
, ![]()
. Oblicz długości wszystkich wektorów oraz kąt między wektorami ![]()
i ![]()
..
2. Wyznaczyć wektory ![]()
oraz ![]()
, które można otrzymać z podanych wektorów ![]()
:
![]()
, ![]()
, ![]()
![]()
, ![]()
. Oblicz długości wszystkich wektorów oraz kąt między wektorami ![]()
i ![]()
..
3. Wyznaczyć wektory ![]()
oraz ![]()
, które można otrzymać z podanych wektorów ![]()
:
![]()
, ![]()
, ![]()
![]()
, ![]()
. Oblicz długości wszystkich wektorów oraz kąt między wektorami ![]()
i ![]()
4. Rowerzysta jechał z Gliwic do miasta Zabrza. Połowę drogi przejechał z prędkością v1=10km/h. Następnie przez pierwszą połowę pozostałego czasu podróży jechał z prędkością v2=15km/h, a w ciągu drugiej połowy tego czasu szedł pieszo z prędkością v3 = 5 km/h. Oblicz średnią prędkość człowieka w tej podróży.
5. Ruch punktu materialnego opisany jest układem równań: x(t) = rsin(ωt) i y(t) = rcos(ωt), przy czy r i ω są stałe Wyznaczyć składowe prędkości i przyspieszenia. Wykazać, że torem punktu jest okrąg o promieniu r. Wyznaczyć wartość bezwzględną wektora prędkości i przyspieszenia
6. Cząstka porusza się wzdłuż osi x zgodnie z równaniem: x(t) = 3 - 12t +3t2, x wyrażone jest w metrach, a t w sekundach. Ile wynosi prędkość i przyspieszenie cząstki w chwili t = 1s? Czy w jakiejś chwili prędkość cząstki jest równa 0?
7. Znaleźć prędkość i przyspieszenie w ruchu na płaszczyźnie (x, y) opisanym równaniami:
x(t) = Acos(Bt2), y(t) = A sin(Bt2), gdzie A, B są stałymi. Znaleźć równanie toru. Jaki to jest ruch?
8. Ruch punktu opisują równania parametryczne x(t) = ct, y(t) = a +bt2, przy czym a, b, c są stałe. Obliczyć
składowe prędkości i przyspieszenia. Wyznaczyć tor punktu przyjmując: a = 0, b = g/2, c = v0.
9. Przedmiot wyrzucono pod kątem α do poziomu z wysokości H z prędkością początkową v0 (rysunek
poniżej). Obliczyć czas lotu i prędkość w momencie upadku na podłoże.
10. Przedmiot umieszczony w początku układu odniesienia rzucono pod kątem a do poziomu z prędkością
początkową v0. Zapisać równania przebytej drogi w dwóch wzajemnie prostopadłych kierunkach: x=x(t) i
y=y(t). Zakładając, że równania te, zapisane zaraz po starcie (ruch obserwowany w kierunku pionowym jest
ruchem jednostajnie opóźnionym zaraz po starcie) są ważne przez cały czas ruchu, udowodnić, że torem ruchu
jest parabola.
11. Zmierzone prędkości elektronu na kolejnych odcinkach prostoliniowych wynosiły: v1=100m/s,
s1=10-8m, v2=110m/s, s2=2.10-8m, v3=105m/s, s3=1.5.10-8m, v4=108m/s, s4=1.3.10-8m. Ile wynosiła prędkość średnia?
12. Kierowca samochodu zauważył przeszkodę na jezdni i zaczął hamować w chwili gdy szybkościomierz wskazywał 72 km/h. Po przebyciu przez samochód drogi s= 30 m, szybkościomierz pokazał v2=36 km/h. Zakładając, że siłą hamująca miała stałą wartość podczas hamowania oblicz: wartość przyspieszenia samochodu oraz czas hamowania pojazdu na drodze s.
Zadania dodatkowe:
1. Piłka została rzucona pionowo do góry z szybkością początkową 20 m/s.
a) po jakim czasie osiągnie maksymalne położenie?
b) jak wysoko wzniesie się piłka?
c) po jakim czasie piłka będzie na wysokości 16 m nad ziemią?
2. Elektron porusza się po linii prostej, a wartość jego prędkości chwilowej zmienia się zgodnie z równaniem
V=At2-Bt. Czy jest możliwe, że elektron w pewnym momencie się zatrzyma? Dane: A=20 m/s2, B=15 m/s2.
Wykonaj wykres zależności prędkości od czasu. Ile wynosi przyspieszenie cząstki?
3. Udowodnij podane zależności:
![]()
Oznaczenia:
![]()
- iloczyn wektorowy, ![]()
- iloczyn skalarny, ![]()
- wersory (wektory jednostkowe) osi Ox, Oy i Oz
![]()
- długość wektora (moduł) ![]()
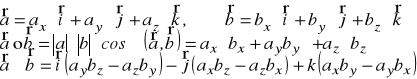
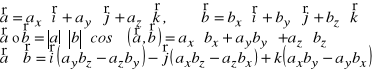
Wyszukiwarka
Podobne podstrony:
Zestaw1, POLIBUDA, Fizyka (semestr 1)
Zestaw1, POLIBUDA, Fizyka (semestr 1)
pochodne, POLIBUDA, Fizyka (semestr 1)
gleboznawstwo- wyklady, Polibuda, OŚ, Semestr IV, Gleboznawstwo
ZRODLA I ROZPRZESTRZENIANIE ZANIECZYSZCZEN-WYKŁAD, Polibuda, OŚ, Semestr IV, Źródła i rozprzestrzeni
wyklad2 (1), Polibuda (MiBM), Semestr III, III semestr, Skowron, III semestr, obróbka skrawaniem
Zestaw zagadnień, Budownictwo PŁ, I semestr, Fizyka, Wykłady
kationy, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogolna nie organiczna
308t, Polibuda, II semestr, Fizyka laboratoria, Fizyka- laboratoria, Laborki- inne2
Chemia mat. bud, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, 1sem.chemia.laborki, Chemi
sciaga na egzmin, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, 1sem.chemia.laborki
sprawko z osadów, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogolna nie organic
6!!!!!!!!!, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki
hydroliza, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, 1sem.chemia.laborki, Chemia - I
sprawko cw1, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogolna nie organiczna
sprawozdanie z cw 4, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogolna nie orga
Wyklad16, 1 STUDIA - Informatyka Politechnika Koszalińska, muniol, I rok, Fiza-Elektronika laborki,
Odczyn roztworów wodnych soli, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogoln
więcej podobnych podstron