Fizyka Matematyczna - Wykłady.

Wykład 1

1. Elementy Rachunku Wariacyjnego

1. Przykłady prowadzące do rachunku wariacyjnego

1. Zagadnienie Brachistochrony

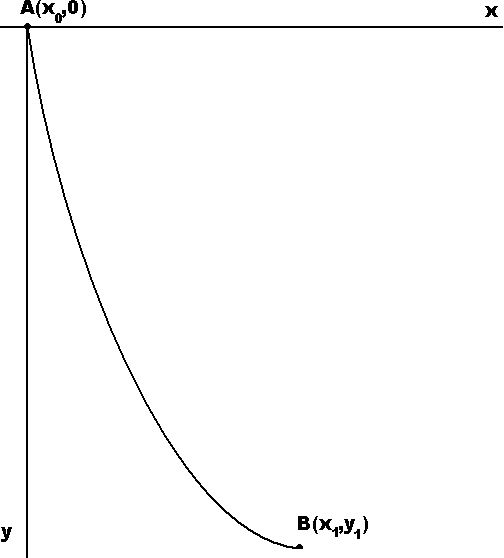
Z pośród krzywych przechodzących przez punkt A i B nie leżące na jednym poziomie, znaleźć tę krzywą, po której poruszający się punkt materialny pod wpływem siły ciężkości osiągnie w najkrótszym czasie punkt B.

Jest to zagadnienie Bardzo stare (1696r.)




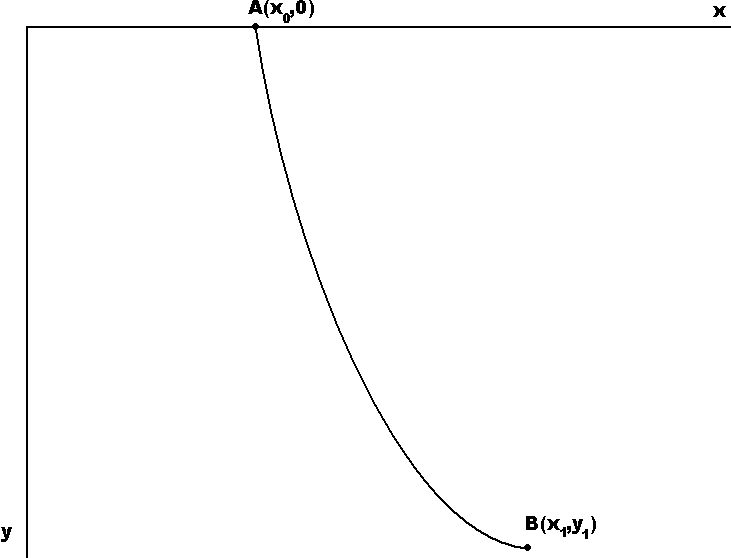
T - czas przejścia z A do B.

2. Zagadnienie izotelemetrii


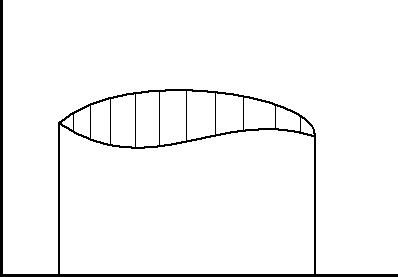
Krzywa zamknięta o długości l

Jaki kształt ma przyjąć krzywa, aby pole było największe.

L - krzywa o długości l

Wykorzystujemy wzór Blina.










3. Zagadnienie krzywych geodezyjnych




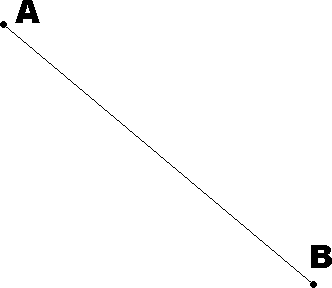
Dwa punkty na powierzchni nie koniecznie płaszczyźnie. Po jakiej krzywej należy się poruszać, aby droga była najkrótsza.

W przypadku kuli jest to np. po kole wielkim.

2. Pojęcia podstawowe rachunku wariacyjnego.

1. Funkcjonał

Y - zbiór elementów;
, R - zbiór liczb rzeczywistych


Funkcjonał to przyporządkowanie elementów zbioru Y elementom zbioru R → na zbiorze Y przyporządkowany jest funkcjonał
Przykłady funkcjonałów:




na początku będziemy się zajmować tylko funkcjonałami zaznaczonymi w ramkę powyżej.

2. Przestrzeń liniowa

Zbiór elementów, gdzie elementy mają własności:




3. Przestrzeń unormowana


x jest elementem przestrzeni Norma jest długością wektora




odległość pomiędzy punktami x, y:




przestrzeń funkcji jednej zmiennej w przedziale od A do B:












4. Otoczenie funkcji


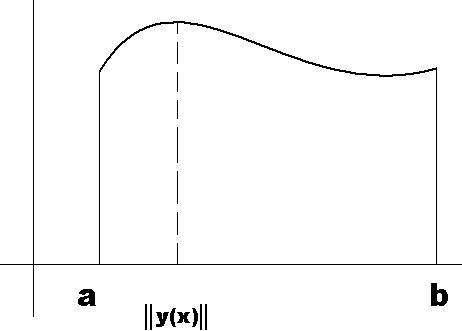
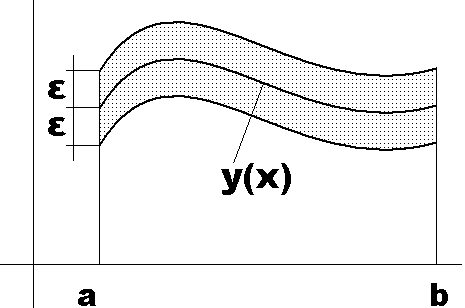
Mamy funkcję y(x)

Otoczeniem
funkcji
nazywamy każdą funkcję






5. Ekstremum funkcjonału


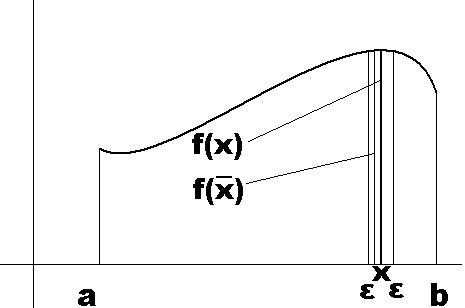
funkcjonał osiąga ekstremum na funkci y wówczas gdy istnieje otoczenie
że dla każdego
wyważenie
ma stały znak.

Wykład 2

6. Funkcjonał ciągły

Funkcjonał J jest ciągły gdy dla odległości funkcji
dążącej do zera to rużnica funkcjonałów
też dąży do zera




7. Funkcjonał liniowy

Funkcjonał J nazywamy liniowym gdy zachodzi:


Będziemy zajmować się funkcjami typu:




8. Wariacja funkcji


h(x) - nazywamy wariacją funkcji

9. Wariacja Funkcjonału




Wariacją funkcjonału (różniczką funkcjonału) nazywamy liniową ze względu na h przyrostu funkcji.

3. Warunek konieczny istnienia ekstremum funkcjonału.

Warunkiem koniecznym aby funkcjonał J[y] osiągał ekstremum na krzywej y jest aby jego wariacja δJ na tej krzywej była równa 0




minimum:


zakładając że:


Przypomnienie: (rozwijamy w szereg Taylora)




i piszemy:


Więc wariacja funkcjonału:


Warunek konieczny na istnienie ekstremum funkcjonału:




nie znamy h.

4. Równanie Eulera

1. Lemat Lagrange'a

Jeżeli funkcja f(x) jest funkcją ciągłą i dla dowolnej funkcji ciągłej h(x) posiadającej ciągłą pochodną i spełniającej warunki h(a)=h(b)=0 zachodzi równość
to f(x)≡0

Na końcach przedziału h(x)=0.

Jeżeli mamy punkty
to na pewno jest przedział
to ten przedział jest dodatni




2. Twierdzenie (wykorzystujące Lemat Lagrange'a)

Warunkiem koniecznym na to aby funkcjonał
określony na zbiorze funkcji ciągłych posiadających ciągłe 2 pochodne i spełniających warunki y(a)=A i y(b)=B osiągnęła ekstremum jest aby ta funkcja spełniała równanie różniczkowe drugiego rzędu
i warunki brzegowe y(a)=A i y(b)=B.





1. Całka pierwsza




2. Przykład: Zagadnienie Brachistochrony








Pamiętając że:




Rozwiązanie całki:




3. Analogie w badaniu funkcji i funkcjonałów

	Funkcja	Funkcjonał
	Przyporządkowanie liczbom x liczby y	Przyporządkowanie funkcjom liczby J
	Mamy x i bliską liczbę czyli przyrostem x nazywamy	Przyrost funkcji albo wariacja funkcji
	Przyrost funkcji	Przyrost funkcjonału
	jeżeli osiąga ekstremum
	Różniczkę funkcji możemy obliczyć z:

6. Funkcjonał zależny od n funkcji

Fizyka Matematyczna - Wykłady strona 1 z 7

























---