1.Grawitacja źródłem jest istnienie masy, jedno z najsłabszych oddziaływań, słabe natężenie(10^-36 - 10^-40),zasięg ∞

G- stała grawitacji,

r_j- wektor jednostkowy wzdłuż promienia Ciała obdarzone masą przyciągają się wzajemnie. F = Gm₁m₂/ r² gdzie: G - stała grawitacji Prawo powszechnego ciążenia możemy zapisać za pomocą wektora r, którego początek znajduje się w środku masy m₁: F =- Gm₁m₂/ r³ r. Jest to wektorowa postać prawa powszechnego ciążenia. Znak „-` wskazuje na przeciwne zwroty wektorów F i r. Siły grawitacyjne są siłami przyciągającymi. Natężenie pola grawitacyjnego jest równe stosunkowi siły działającej na masę do jej wartości γ =F / m.=-GM / r³ r Bardzo ważną cechą siły grawitacyjnej jest to, że jest siłą zachowawczą, a zatem praca w polu siły ciężkości nie zależy od kształtu i długości drogi, lecz od położenia punktów początkowego i końcowego. Potencjał pola definiujemy jako stosunek energii potencjalnej ciała w danym polu do wielkości charakteryzującej zachowanie się ciała w tym polu. Dla pola grawitacyjnego będzie to masa ciała, a wzór na potencjał przyjmuje postać:

V(r) = E_p (r) / m = - GM / r

2.Elektromagnetyczne: żródłem jest istnienie ładunku elektrycznego(+,-), zarówno elektrostatyczne jak i magnetyczne, ich suma daje oddziaływanie, natężenie

10^-2,zasięg ∞

Praca przypadająca na jednostkę ładunku nosi nazwę siły elektromotorycznej (SEM) ε. ε =1/q ∫Fds Korzystając z definicji natężenia pola elektrycznego (E=F/q), wyrażenie powyższe możemy zapisać w postaci ε =∫Eds

3.Oddziaływanie silne: źródłem są składniki jądra Hadrony(neutron ⁰₁n, proton¹₁p, mezonπ)najsilniejsze oddziaływanie 1, zasięg (jądro atomowe ) 10^-15

Natężenie 10^-15 dla cząstek elementarnych. Zakres oddziaływania 10^-18,10^-15 . Nośnikami są mezony.

4.Jednorodność przestrzeni a zasada zachowania pędu: Przypuśćmy, że suma sił zewnętrznych działających na układ jest równa zero, wtedy na podstawie równania
, przy założeniu

Jeżeli wypadkowa sił zewnętrznych działających na układ jest równa zero, to całkowity wektor pędu tego układu pozostaje stały. Z III zas. dynam. Newtona ΣF_i = 0 , F_A=-F_B

Σp_i = const

Prawa zachowania energii i masy są słuszne w każdym inercjalnym układzie odniesienia, Jeżeli pęd w zderzeniu jest zachowany. Mówimy, że wielkości te są niezmiennicze względem transformacji Galileusza. Brak jest jednorodnych punktów. ∑F = 0,

5.Izotropowość przestrzeni a zasada zachowania momentu pędu: Stosunek zmiany całkowitego momentu pędu związanego z inercjalnym układem odniesienia do czasu, w którym ta zmiana nastąpiła jest równy sumie momentów sił zewnętrznych działających na ten układ
gdy M_z=0 , to L=const

M = r x F , L = r x p

Przyjmuję jednorodność przestrzeni wówczas p = const, zakładam E = const , ze względu na Δr (przesunięcie)

p = const

do rys.

:

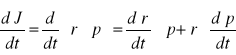
Lecz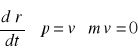

Oraz: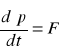
stąd: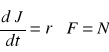
Jeżeli moment siły
, to szybkość zmian momentu pędu
i co za

tym idzie, sam moment pędu jest stały.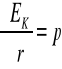
to jest pęd

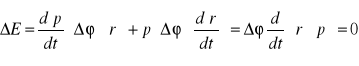
6.Nizmienniczość względem translacji w czasie a zasada zachowania energii: Cząstka o masie m w układzie inercjalnym. W chwili t = 0 została przyłożona siła
, działająca wzdłuż osi x. Ruch cząstki opiszemy, korzystając z drugiej zasady Newtona
Wtedy prędkość cząstki po czasie t

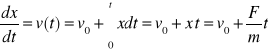
Skąd

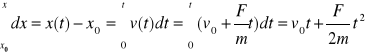
Po przekształceniu otrzymamy

Lewa strona tego wyrażenia jest pracą wykonaną nad cząstką przez stałą siłę zewnętrzną, prawa strona jest zmianą energii kinetycznej cząstki. Mówimy, że na wysokości h ciało ma energię potencjalna względem powierzchni ziemi

E_p = mgh i jest ona równa zmianie energii kinetycznej

Załóżmy że v₀ = 0 oraz przyjmijmy, że v oznacza prędkość chwilową po przebyciu drogi h - x. Wówczas

Jeżeli ruch rozpoczyna się z wysokości h, to energia całkowita E = const dla każdego x. W ten sposób określiłem zasadę zachowania energii:

E_K + E_P = E = const.

a całkowita praca wykonana na drodze AB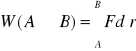
dla
i m = const.

otrzymamy:

Wynika stąd, że praca wykonana nad cząstką swobodną przez dowolną siłę zewnętrzną jest równa zmianie energii kinetycznej cząstki. Praca po drodze zamkniętej jest równa zeru.

7.Układy inercjalne, transformacja i zasada względności Galileusza: Układy w których obowiązują zasady dynamiki Newtona nazywamy układami inercjalnymi, a układy w których nie obowiązują układami nie inercjalnymi.

- układy inercjalne to takie układy odniesienia, które spoczywają lub poruszają się ruchem jednostajnym prostoliniowym.

-układy nie inercjalne poruszają się ruchem jednostajnie przyspieszonym.

Transformacja Galileusza: Dwóch obserwatorów bada jakieś zjawisko w dwóch różnych układach odniesienia. Aby porównać uzyskane przez nich wyniki, musimy je przekształcić (dokonać transformacji z jednego układu odniesienia do drugiego) . W fizyce obowiązuje hipoteza niezmienniczości Galileusza, według której podstawowe prawa fizyki są jednakowe we wszystkich inercjalnych układach odniesienia. Według tej hipotezy obserwator, który znajduje się w pomieszczeniu bez okna, nie może stwierdzić za pomocą żadnego doświadczenia, czy w jest w spoczynku czy w ruchu jednostajnym względem gwiazd stałych. Dwaj obserwatorzy poruszający się względem siebie i obserwujący jakieś zjawisko mogą je opisać inaczej. Z hipotezy niezmienniczości wynikają reguły transformacji położenia i prędkości z układu spoczywającego XYZ(nieprimowanego) do układu X`Y`Z`(primowanego), poruszającego się z prędkością

Między współrzędnymi zmierzonymi przez obu obserwatorów istnieje związek: x` = ut, y` = y, z` = z, t` = t lub wektorowo

Równania te określają związek miedzy obserwacjami dokonanymi w dwu różnych układach inercjalnych. Jeżeli punkt P porusza się to jego prędkość
, zmierzoną w układzie X`Y`Z`, otrzymamy, różniczkując względem czasu równanie(4)

Stąd
gdzie: v jest prędkością punktu zmierzoną przez obserwatora w układzie spoczywającym XYZ. Ponieważ u=const ,zatem:
więc równanie

Równość czasów w obu układach t`=t jest w granicach dokładności pomiarów zgodna z doświadczeniem dla v<<c. Zestawienie wszystkich równań transformacyjnych z przekształceń Galileusza:
8.Postulaty teorii względności:

. -prawa fizyki mają jednakowa postać we wszystkich układach inercjalnych odniesienia.

Nie istnieje żaden wyróżniony inercjalny układ odniesienia.

-prędkość światła jest jednakowa we wszystkich układach inercjalnych odniesienia i wynosi 2,988*108m/s = 300.000km/s

9.Transformacja Lorentza: Weźmy pod uwagę dwa układy inercjalne S i S`, których osie x i x` są do siebie równoległe, a początki O i O` pokrywają się w układzie S ze stałą prędkością v , zwróconą zgodnie ze zwrotem osi x. Gdy pewne zdarzenie zaobserwowane w układzie S ma współrzędne x,y,z,t, to odpowiednie jego współrzędne w układzie S` wynoszą x`,y`,z` ,t`. Układy odniesienia wybieramy w taki sposób, żeby zawsze y` = y i z` = z i tymi współrzędnymi nie będziemy się zajmować. Mamy więc w każdym układzie jedną współrzędną przestrzenną (x lub x`) i jedna współrzędną czasową (t lub t`).

Równanie czoła fali kulistej :

x²+y²+z²=c²t²

x'²+y'²+z'²=c²t'²

stosuję podstawienia

x' = x - v t

y' = y

z' = z

t' = t + f x

c't' - promień kuli

podstawiam wartości i rozwiązuję układ równań , przy czym 2c²f + 2v = 0 ⇒

f = -(v / c²) , współczynnik

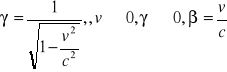
x' = γ( x - v t) x = γ( x' +vt')

y' = y y = y'

z' = z z = z'

t' = γ( t - (v/c²)x) t = γ( t'- (v/c²)x')

10Skrócenie długości

mamy dwa układy s i s', mierzymy długość w obydwu układach : l'- długość zmierzona przez obserwatora w ruchomego ,l- opisuje długość jaką zaobserwuje obserwator nie będący w ruchu ,gdzie :

l₀ = x₂ - x₁ , l' = x₂' - x₁'

l₀=x² - x¹= γ(x₂'+vt')-γ(x₁'+vt') =γ(x₂'-x₁')

l'=l₀/γ =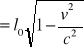
ciało obserwowane w ruchu jest „krótsze” od ciała w spoczynku

12.Transformacja prędkości:

Załóżmy, że układ S` porusza się z prędkością v względem układu S, równolegle do jego osi x. Niech cząstka porusza się z prędkością u' względem układu S`.

ϖ - prędkość punktu P obserwowana z układu nieruchomego S (gdzie :ϖ_x = dx / dt , ϖ_y = dy / dt ) . Z założeń mamy

x = γ ( x' + vt' )

dx = γ ( dx' + vdt' )

t = γ ( t' + v/c² x' )

dt = γ ( dt' + v/c² dx' )

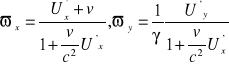
np. Gdy U'_x = c, to ω_x = c , c - to niezmiennik transformacji Lorentza 13.Masa relatywistyczna, energia w teorii względności: m. = γm₀ - masa ciała kiedy się porusza, nie jest równa masie ciała kiedy jest w spoczynku. Zmiana masy jest wynikiem płynięcia czasu w dwóch układach. Energia relatywistycna: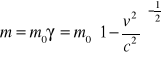

V - małym:

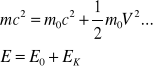
m - całkowita masa jest cał. energią zawartą w masie, m₀c² - energia spoczynkowa, 1/2m₀V² - prędkość ruchu, E - energia całkowita, E₀ - energia spoczynkowa,

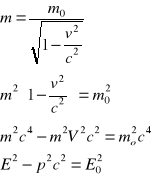
dla E₀ = 0, E = p ⋅ c

p = mV = E / c² V = (p / c) ⋅ V,

V⇒ c - wartość prędkości jest równa wartości c.

14.Związek między masą a energią: Wychodzę z wzoru na relatywistyczną masę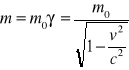

Rozwijając w szereg dwumian w nawiasie ,dostaję: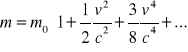

Ze wzoru tego wynika, że gdy v jest małe, szereg jest bardzo szybko zbieżny i wszystkie dalsze wyrazy poza pierwszymi dwoma można pominąć, czyli:

Ponieważ mv² / 2 jest klasyczną energią kinetyczną, można powiedzieć, że przyrost masy:
,

związany z ruchem ciała, jest równy jego energii kinetycznej podzielonej przez kwadrat prędkości światła:

Całą masę ciała można zdefiniować jako całkowitą energię zawartą w ciele podzieloną przez c² .Mnożąc przez c² wyrażenie na masę w ruchu otrzymamy:

Lewa strona równania przedstawia całkowitą energią ciała: E = mc². Wyrażenie E² - p²c² = E_o² , nazwane jest niezmiennikiem transformacji Lorentza. Rozwijając lewą stroną równania i pamiętając o tym że energia całkowita jest sumą energii spoczynkowej E₀ i kinetycznej T: E = E_o + T otrzymamy:

(E - E₀)(E + E₀) = p²c² ale E - E₀ = T to T(T + 2E₀) = p²c² Otrzymałem związek między pędem relatywistycznym a energią kinetyczną wyrażony w postaci:
Otrzymaliśmy związek ,że v = c. Zatem cząstki o masie spoczynkowej równej zeru muszą poruszać się z prędkością równą prędkości światła .

15.Oscylator harmoniczny:

Aby zaistniał ruch potrzebna jest siła :

F = -kx (x-wychylenie, k-sprężystość ukł)

m*a = -kx , to a + k/m x =0 , a -przyspie.

Możemy również zapisać :

x(t) = Asin (ωt + f₀)

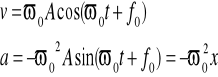
a stąd:

A - amplituda drgań

ωt +f₀ - faza drgań

ω₀ - prędkość kołowa , pulsacja , częstość

Oscylator tłumiony :W rzeczywistym oscylatorze w wyniku działania tarcia amplituda drgań maleje stopniowo aż do zera.

F = ma lub -kx - b(dx/dt) =m(d²x/dt²)

-b(dx/dt) - siła tłumiąca, jeżeli b jest mała:

lne^βT = βT - log. deklement tłumienia

β = r/2m - współczynnik tłumienia

16.Rodzaje fal, równanie fali płaskiej i sferycznej:

y = f(x - vt) ogólne równanie fali dowolnego kształtu biegnącej w prawo

y = f(x + vt) ogólne równanie fali dowolnego kształtu biegnącej w lewo

Fala szczególna (kształt sinusoidalny)

Y = y_m sin 2πx / λ : y_m - max wychylenie (ampituda) ,λ-długość fali

Z biegiem czasu fala przesuwa się w prawo z prędkością fazową

λ = v T ; T - okres

podstawiając zależność λ do równania fali otrzymamy : k =2π/λ - liczba falowa

y = y_msin (kx+ϖt) - sinusoida poruszająca się w prawo

y = y_msin (kx-ϖt) - sinusoida poruszająca się w lewo

17.Interferencja fal: Zgodnie z zasadą superpozycji przemieszczenie dowolnej cząsteczki w ustalonej chwili jest sumą przemieszczeń wywołanych przez poszczególne fale. Wychylenia z położenia równowagi wywołane przez dwie fale w punkcie leżącym w odległościach x₁ i x₂ od obu źródeł wynoszą odpowiednio: y₁ = A₁sin(ϖt - kx₁), y₂ = A₂sin(ϖt - kx₂). Wychylenie wypadkowe jest sumą algebraiczną wychyleń składowych: y = y₁ + y₂ = A₁sin_­(ϖt - kx₁) + A₂sin(ϖt - kx₂) = Asin(ϖt - ϕ) gdzie A oznacza amplitudę fali wypadkowej. Jeżeli fale o jednakowej częstości nakładają się na siebie i mają stałą w czasie różnicę faz, to: Δϕ = k(x₂ - x₁). Takie fale nazywamy spójnymi lub koherentnymi , a ten przypadek superpozycji fal - interferencją fal.

18.Fale stojące: Jeżeli nakładają się na siebie dwie fale biegnące w przeciwnych kierunkach, to:

y = Asin(ϖt - kx) + Asin(ϖt+kx) = A[sin(ϖt - kx) + sin(ϖt + kx)] a po przekształceniu: y = 2Asinϖt ⋅ coskx = [2Acoskx]sinϖt = A`sinϖt. Nastąpiło rozseparowanie zależności przestrzennej i czasowej w równaniu fali. Otrzymane równanie opisuje falę stojącą. Fala stojąca może powstać w wyniku nałożenia się fal padającej i odbitej od granicy ośrodków. Przy fali odbitej zachodzą następujące zależności: mamy falę padającą y₁ = Asin (ϖt - kx) i odbitą y₂ = Asin(ϖt + kx + ϕ). Wychylenie wypadkowe wynosi: y = y₁ - y₂ = 2Acos(kx +ϕ / 2)sin(ϖt + ϕ / 2

19.Interferencja światła: Interferencja światła jest głównym świadectwem jego falowej struktury. Możemy ją obserwować w następujących warunkach: 1) ciągi falowe muszą się przecinać, 2) ciągi falowe muszą być spójne lub koherentne. Różnica faz między źródłami fal musi być stała w czasie. Gdy zaistniała między nimi różnica dróg optycznych jest całkowitą wielokrotnością długości fali w próżni, wiązki spotykają się zgodnymi fazami i wzajemnie wzmacniają. Jeśli zaś różnica dróg optycznych między wiązkami jest równa nieparzystej wielokrotności połówek długości fali w próżni, fale spotykają się przeciwnymi fazami i osłabiają. Warunek na interferencyjne wzmocnienie ma postać: Δl = kλ, zaś na osłabienie: Δl = (2k + 1) λ / 2 gdzie: k - długość fali świetlnej w próżni, Δ - różnica dróg optycznych.

20.Dyfrakcja: Jest to zjawisko polegające na uginaniu się promieni świetlnych przechodzących w pobliżu przeszkody, takiej jak np. brzeg szczeliny. Rozróżnia się dwa typy dyfrakcji: 1) dyf. Fresnela - gdy źródło lub ekran leżą w skończonej odległości id szczeliny (czoła fal padającej na nią nie sa płaskie), 2) dyf. Fraunhofera - zarówno źródło, jak i ekran leżą nieskończenie daleko od szczeliny, obie rozważane fale są płaskie, ich promienie są wzajemnie równoległe. Dyfrakcję Frau. uzyskuje się stosując układ soczewek.

Wiązka światła wychodząca ze źródła Z po przejściu przez soczewkę S₁ tworzy falę padającą na szczelinę S₂. Wówczas wszystkie promienie docierają do środkowego punktu w tej samej fazie. W punkcie leżącym naprzeciwko środka szczeliny otrzymujemy maksimum dyfrakcyjne zerowego rzędu. Dyfrakcja Fru. Na pojedynczej szczelinie:

min : a/2 sinϕ = λ/2

min : a sinϕ = nλ

max : a sinϕ = ( n +0,5 )λ

21.Polaryzacja światła:

Polaryzator rozdziela naturalne światło na zbiór. Zjawiska dotyczące polaryzacji :

*dichroizm - selektywne pochłanianie

*odbicie

Płaszczyzna drgań wektora świetlnego w wiązce jest prostopadła do płaszczyzny padania. Całkowita polaryzacja wiązki odbitej następuje wtedy, gdy wiązka ta jest prostopadła do wiązki załamanej, czyli gdy β = 90 - α . Stąd:

czyli: n = tgα. Kąt spełniający ten warunek nazywamy kątem całkowitej polaryzacji. *dwójłomność:

Zjawisko to polega na tym, że wiązka światła niespolaryzowanego padająca na kryształ anizotropowy ulega załamaniu na powierzchni granicznej rozdwojeniu na dwie wiązki. Dwie wiązki spolaryzowane zwyczajna i nadzwyczajna.W czystych kryształach dwójłomnych każda wiązka załamana jest w 100% spolaryzowana.

n_zw + n_nz = Δn

*rozoroszenie

23.Prawo Kulomba: Dwa nieruchome ładunki elektryczne q oraz Q oddziałują na siebie siłą daną wzorem:

Lub w zapisie wektorowym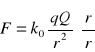

Stała k_o zależy tylko od układu jednostek. W układzie SI: k₀ = 1 / (4πε_oε). Stała: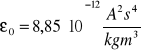

Kulomb jest ładunkiem, który na drugi taki sam ładunek działa z odległości 1 [m.] siłą równą 9 ⋅ 10⁹ [N]. Kulomb jest jednostką pochodną ampera. Wartość jednego kulomba ma ładunek elektryczny, przepływający w czasie jednej sekundy przez przewodnik, w którym płynie prąd o natężeniu jednego ampera. Przyjmuje się że siła jest dodatnia dla ładunków równoimiennych, a ujemna dla różnoimiennych. Zakres stosowalności prawa Kulomba rozciąga się od 10^-15 [m.]. do kilkudziesięciu lat świetlnych.

24.Ruch cząsteczek naładowanych w polu elektromagnetycznym: Równanie cząstki swobodnej wpadającej z prędkością
w pole magnetyczne o indukcji
ma postać: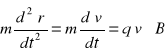

E_k = const. Prędkość cząstki ma stałą wartość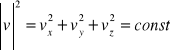

Równanie cząstki w postaci skalarnej ma postać: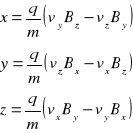

Zakładamy, że pole magnetyczne jest równoległe do osi z:

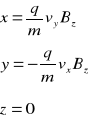
Rozwiązanie ostatniego równania ma postać:v_z=const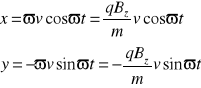

A stąd po przekształceniu możemy wyznaczyć prędkość kątową

Uwzględniając, że w chwili początkowej t_o cząstka znajdowała się w punkcie o współrzędnych (x_o,y_o,z₀) oraz v / ϖ = r, otrzymamy:

x = x₀ - rcosϖ_ct

y = - y_o + rsinϖ_ct

z = - z_o + v_zt

Torem cząstki jest spirala linii sił pola magnetycznego o stałym skoku zależnym od v_z. B_r = mv / q gdzie mv jest składową pędu w płaszczyźnie prostopadłej do B.

26.Pole magnetyczne i jego względność: Dwa równoległe przewodniki, przez które płynie prąd, przyciągają się lub odpychają się. Obserwując zamiast dwóch przewodników strumień swobodnych elektronów w pobliżu przewodnika z prądem, również stwierdzimy odchylenie biegu elektronów po włączeniu prądu. Można więc przyjąć, że w przestrzeni otaczającej przewodnik z prądem znajduje się pole magnetyczne. Pole to opisujemy za pomocą wektora indukcji magnetycznej
, zdefiniowanego przez siłę elektrodynamiczną działającą na poruszający się ładunek:

w próżni

Pole magnetyczne jest polem bezżródłowym , jest polem wirowym. Nie mam szans na otrzymanie pojedynczego bieguna N lub S .

Cyrkulacja

27.Równanie Maxwella: Maxwell traktował przestrzeń jako ośrodek materialny - eter. Jeśli w przestrzeni nie ma żadnej dotykalnej materii ,prąd przesunięcia płynie w jakimś ośrodku.

Postać różniczkowa: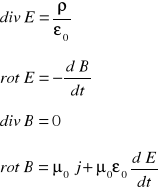

μ₀ i ε₀ - stałe które charakteryzują własności próżni w sensie magnetycznym ( gdy nie ma materii)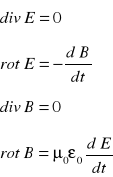

Są to cztery sprzężone równania różniczkowe cząstkowe .Stosują się one do każdego punktu przestrzeni pola elektromagnetycznego. W próżni gęstość ładunku ρ oraz prądu I równa się zero.

Maxwell jako pierwszy zasugerował, że światło jest falą elektromagnetyczną o określonym zakresie częstotliwości.

28.Paczki falowe:

Paczka falowa jest obrazem matematycznym cząstki.σ_x - odchylenie standartowe funkcji gausowskiej(mam ogólnie więcej niż 50% szans)

V_cz=dx/dt (klasyczny) W paczce prędkością jest prędkość grupowa. V_g=dω/dk (opis falowy ) ..nie pisz !!! (-σ_p , +σ_p)

[ σ_p *σ_x ≥ h ] Jeżeli iloczyn wartości błędu położenia i pędu jest równy h to jest to zasada nieoznaczoności Heinzenberga .Prawdopodobieństwo znalezienia cząstki w przedziale między x = - σ_x i x = +σ_x jest gaussowską funkcją „błędu”, a σ_x jest odchyleniem standardowym. Wielkość tę nazywamy nieokreślonością położenia. Funkcję zlokalizowaną w ten sposób nazywamy paczką fal.

29 Zasada nieokreśloności Heisenberga:

ΔxΔp = hΔνΔt

ΔxΔp - iloczyn położenia i pędu

ΔνΔt - odwrotność czasu ⇒częstość ⇒ten iloczyn równy jest 1

ΔxΔp ≥ h - zas. Nieozn. Heizenberga (własność natury)

skoro z idealną dokładnością nie możemy podać obu wielkości to określamy tylko jedynie prawdopodobieństwo ( jak Δx określę dokładnie to Δp→∞)

ΔxΔp ≥ h te wielkości są ze sobą

ΔtΔE ≥ h sprzężone (wstęp do

ΔϕΔL ≥ h mech. Kwantowej)

30. Równanie Schrodingera: Na cząstkę może działać siła zewnętrzna, której odpowiada energia potencjalna U(x)., Ponieważ energia:

jest stała, więc jeśli U rośnie w miarę wzrostu x, to p będzie malało, co oznacza, że długość fali będzie wzrastała. Funkcja falowa musi mieć zmienną długość fali. Funkcja falowa, której długość fali rośnie w miarę zwiększania się x. Ścisłą postać funkcji ψ(x) o zmiennej długości fali znajduje się rozwiązując równanie różniczkowe zwane równaniem Schrodingera. W obszarze, w którym energia potencjalna U₁ jest różna od zera, funkcja ψ(x) spełnia równanie:

Ponieważ równanie na funkcję ψ(x) ma taką samą postać dla U₂,..,U_j, a dowolną funkcję U(x) można przybliżyć funkcją schodkową o bardzo małych schodkach U_j, więc U₁ możemy zastąpić funkcją U(x) i otrzymujemy :

Jest to równanie niezależne od czasu w jednym wymiarze. Stosuje się ono do ciał nierelatywistycznych wtedy, kiedy rozkład prawdopodobieństwo nie zmienia się w czasie. Warunki brzegowe: Jeżeli cząstka jest związana w studni potencjału, to prawdopodobieństwo znalezienia jej z dala od studni jest równe zeru. Stąd wynika warunek brzegowy: dla dużych wartości

x prawdopodobieństwo znalezienia cząstki jest równe zeru.

31.Studnia potencjału: Równanie Schrotingera można zastosować do rozwiązywania zagadnień cząstki w studni potencjału, której ściany mają skończoną wysokość U₀ : Musimy znaleźć takie funkcje falowe ψ(x), które spełniają warunek brzegowy : ψ(x) → 0 dla dużych x , oraz energię E_n odpowiadającą tym funkcją. W obszarze II równanie Schr. Ma postać:

a jego rozwiązaniami są funkcje: ψ_II = e^-kx oraz e^+kx , gdzie:

Tam gdzie energia kinetyczna jest ujemna, pochodna d²ψ / dx² oraz funkcja ψ mają taki sam znak, a więc funkcja ψ musi się odginać od osi x. Natomiast tam gdzie energia kinetyczna jest dodatnia , ψ(x) będzie zaginała się ku osi x tak jak zagina się fala sinusoidalna.

32.Funkcja falowa i jej interpretacja fizyczna: Równanie ruch fali:

Dla zwykłej cząstki energię mechaniczną E wyrażamy wzorem:

gdzie: p = mv - pęd cząstki, U - energia potencjalna. Energia fali według de Broglie`a dla cząstki o energii wyrażonej powyższym wzorem:

Równanie Schrodingera dla jednowymiarowej fali de Broglie`a niezależnej od czasu:

Równanie Schrodingera w ogólnej postaci uwzględnia zależność funkcji falowej od trzech współrzędnych przestrzennych i od czasu. Jeśli pędowi cząstki p przyporządkowujemy operator
różniczkowania względem współrzędnych przestrzennych, to równanie Schrodingera dla ustalonej fali de Broglie`a możemy napisać w postaci: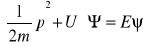

Im silniejsza w danym miejscu fala de Brogli`a, czyli im większa wartość funkcji falowej, tym więcej w tym punkcje elektronów. Kwadrat wartości bezwzględnej funkcji falowej w danym punkcje jest wprost proporcjonalny do prawdopodobieństwa znalezienia tej cząstki w danym punkcie. Samo równanie Schrodingera nie opisuje falowo - korpuskularnej natury cząstek, a jedynie naturę falową. Postulat Borna spełnia rolę równania wiążącego własności falowe z korpuskularnymi. Funkcja falowa jest niemierzalna . Według Borna, fale de Broglie`a są falami prawdopodobieństwa określającego stan materii.

33.Atom wodoru:

Rysuj kształt studni potencjału w której znajduje się elektron . Kształt nie jest już prostokątny ale opisany funkcją 1/r .

Powłoka elektronowa → n

Dla n =1 można przyporządkować tylko jedna liczbę l [ l = 1 - 1 = 0 ]

Graficzny obraz atomu

n = 1 ,2 ,...∞ - główna liczba kwantowa

l = 0,1,...n-1 - poboczna liczba kwantowa

m_l =0,±1,±2....±l - magnetyczna licz kwant

m_s = ± 0,5

34.Liczby i stany kwantowe elektronów:

Liczby kwantowe mogą przybierać tylko całkowite wartości n = 1,2,3..., gdy n=∞ odpowiada stanowi w którym elektron jest całkowicie usunięty z atomu .

*główna liczba kwantowa

n = 1,2,3...∞decyduje o rozmiarze obrazu orbitalnego , wprowadza podział na powłoki ,

*poboczna liczba kwantowa l = 0,1,1...n-1 decyduje o kształcie obrazu orbitalnego , wprowadza podział na podpowłoki

*magnetyczna liczba kwantowa

m_l = 0,±1,±2... ,±l decyduje o orientacji przestrzennej obrazu orbitalnego

*spinowa liczba kwantowa m_s = ,±0,5 jest związana z obrotem elektronów dookoła osi N =2n²

Stany kwantowe

*podstawowy k

*zjonizowany k⁺¹ (wzbudzony)

*najniższego wzbudzenia (nietrwały)

35.Zakaz Pauliego: „w atomie nie może być dwóch elektronów o identycznych wartościach wszystkich czterech liczb kwantowych

36.Laser: Przypuśćmy, że mamy taki zbiór atomów, w których większość atomów znajduje się już w stanie wzbudzonym E_n. Pierwszy foton, który zostanie wyemitowany przemieszczając się w gazie, będzie stymulował sąsiednie atomy do wymuszonej emisji fotonów. Jeżeli na obu końcach zbiornika z atomami znajdują się zwierciadła, to zacznie się reakcja łańcuchowa, która będzie trwała dopóty, dopóki wszystkie atomy nie wypromieniują nadmiaru swej energii. Wszystkie wyemitowane fotony będą miały taką samą fazę. Jeżeli jedno z zwierciadeł jest zwierciadłem częściowo odbijającym i częściowo przepuszczającym promieniowanie, to przechodząca przezeń wiązka będzie wiązką spójną. Wiązka ta będzie stanowiła ciągłą falę sinusoidalną promieniowania elektromagnetycznego dokładnie tak samo, jak promieniowanie elektromagnetyczne wysyłane przez nadajnik radiowy. Aby emisja wymuszona przeważała nad absorpcją, w wyższym stanie energetycznym musi znajdować się więcej atomów niż w niższym stanie. Ośrodkami czynnymi w laserach są gazy, ciała stałe i ciecze, a zakres długości fal promieniowania emitowanego przez lasery jest bardzo szeroki, począwszy od podczerwieni, przez obszar widzialny aż do nadfioletu. Laser pracujący w sposób ciągły pracuje w czterech poziomach. Linia, która pochodzi z lasera ma konkretną długość fali. Światło wysyłane z niego jest ściśle określone. Laser barwnikowy składnikiem wyjściowym jest światło monochromatyczne, które pada na barwniki fluoroscencyjne, barwniki możemy zmieniać i otrzymać różne kolory.

37. Model Bohra: Traktował orbity elektronów jak klasyczne orbity kołowe planet. Zasada, którą odkrył Bohra ,stwierdziła iż moment pędu elektronu musi być całkowitą wielokrotnością
czyli:
Z postulatu Bohra wynika następujący wzór na promień n - tej orbity:

Przyrównując siłę dośrodkową do siły elektrostatycznej otrzymujemy :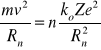

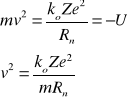
Poziom energetyczny jest zdefiniowany w następujący sposób:

Za pomocą Bohra jest to, że za jego pomocą nie można wyjaśnić widm atomów wieloelektronowych. Elektron porusza się po klasycznej orbicie kołowej, a jego moment pędu jest skwantowany.

38. Teoria pasmowa: Przyjmijmy, że dno studni potencjału jest płaskie i nie ma w nim powtarzających się okresowo wgłębień. Jeżeli uwzględnimy okresową zmienność potencjału, to okaże się, iż dozwolone wartości energii są ograniczone do pewnych pasm energii. Poziomy energetyczne w izolowanej studni prostokątnej wyrażają się wzorem:
gdzie L jest szerokość studni. Zwiększenie n nie zmienia szerokości pasma tak długo, jak długo odległość między studniami pozostaje bez zmian. W opisie rzeczywistego kryształu jednowymiarową studnię prostokątną należy zastąpić trójwymiarową atomową studnią potencjału. Wówczas każdemu stanowi atomowemu będzie odpowiadało pasmo składające się z n poziomów w przypadku, gdy w próbce znajduje się n atomów. Im bliżej siebie będą umieszczone atomy, tym szersze będzie pasmo. W przypadku wiązania metalicznego studnie atomowe leżą tak blisko siebie, że energie zewnętrznych elektronów tworzą pasmo, które nakłada się na inne pasmo. W kryształach o wiązaniu kowalencyjnym, takich jak german czy krzem, odległość wzajemna studni atomowych jest taka, że pasma energetyczne elektronów walencyjnych nie nakładają się na siebie. W krzemie między zapełnionym pasmem zawierającym elektrony walencyjne i następnym wyższym nie zapełnionym pasmem istnieje przerwa energetyczna równa 1,09 eV.

39. Wiązania jonowe: Przy powolnym zbliżaniu do siebie dwa elektrycznie obojętne atomy, to dojdziemy do takiego punktu, w którym zewnętrzny elektron jednego atomu może przeskoczyć na drugi atom i zostać tam związany. Atom z brakującym elektronem zachowuje się jak cząstka o dodatnim ładunku +e, a atom z dodatkowym elektronem jak cząstka o ujemnym ładunku -e. Elektrostatyczna energia potencjalna układu takich dwóch cząstek jest równa U = - k_oe² / R, gdzie R jest odległościom między środkami tych dwóch jonów. Zwane są inaczej heteropolrnymi lub biegunowymi. Zgodnie z prawem Coulomba jony przeciągają się z siłą wprost proporcjonalną do ładunku i odwrotnie proporcjonalną do kwadratu odległości pomiędzy nimi. Ten typ wiązania tworzy się najłatwiej przez połaczenie atomów pierwiastka o niskim potencjale jonizacyjnym wykazujących dużą łatwość wyrzucania elektronów zewnętrznych, z atomami pierwiastków o wysokim powinowactwie elektronowym. O tworzeniu się wiązania jonowego decyduje duża różnica w elektroujemności pierwiastków.

40. Wiązania kowalencyjne: Zwane są jako homeopolarnymi polegają na istnieniu wiążących par elektronów należących jednocześnie do dwóch sąsiadujących z sobą atomów. W wiązaniu kowalencyjnym nie następuje wymiana elektronów, lecz ich uwspólnienie. Wiązanie kowalencyjne jest również wyrazem dążenia do uzyskania przez atomy trwałych, kompletnych powłok elektronowych gazów szlachetnych. Najprostszym przykładem jest wiązanie w cząsteczce wodoru. Wartościowością kowalencyjna pierwiastka w cząsteczce o wiązaniach kowalencyjnych nazywamy liczbę wspólnych par elektronowych dla atomu danego pierwiastka i innych atomów wchodzących w skład cząsteczki.

41. Wiązanie metaliczne: Sieci krystaliczne metali są uporządkowanym zbiorem jonów dodatnich, tzw. rdzeni atomowych metalu pogrążonych gdyby w gazie elektronowym. Wielkość sił wiązania metalicznego jest zależna od energii przyciągania między jonami i elektronami oraz od energii odpychania między samymi elektronami i samymi jonami dodatnimi. Wiązanie metaliczne nie jest kierunkowe. W wiązaniu metalicznym elektrony walencyjne należą jednocześnie do wszystkich atomów całego kryształu. Jest charakterystyczne dla stałego lub ciekłego stanu skupienia.

42. Wiązania Van deer Waalsa: Są to siły wzajemnego przyciągania się cząsteczek. Siły te są wynikiem działania trzech różnych czynników: sił orientacyjnych, sił indukcyjnych, sił dyspersyjnych. Siły orientacyjne polegają na wzajemnym oddziaływaniu na siebie stałych dipoli. W wyniku działania sił orientacyjnych cząsteczki zbliżają się do siebie, przyciągają i często tworzą ugrupowania, których istnienie stwierdzamy w wielu zasocjowanych cieczach polarnych. Siły indukcyjne polegają na wzajemnym oddziaływaniu między stałym dipolem a dipolem przez niego indukowanym w sąsiednich cząsteczkach, czyli dipolem powstałym pod wpływem działania pola elektrycznego dipola stałego. Jeśli cząsteczki nie będące dipolami znajdują się w polu elektrycznym cząsteczki dipolowej, to dodatnie jądra atomowe i ujemne elektrony cząsteczki niedipolowej ulegają przesunięciu w kierunkach przeciwnych, wskutek czego środki ciężkości ładunków dodatnich i ujemnych przestają się pokrywać - powstaje dipol wzbudzony. Siły dyspersyjne: są to siły przyciągające, polegające na wzajemnym wpływie poruszających się elektronów. Układ złożony przez chwilowe położenie elektronu krążącego dookoła jądra nazywamy w danym momencie dipolem elementarnym. Takich elem. Dipoli jest w każdym atomie tyle ile elektronów ma atom.

43. Wiązania wodorowe: Jądro wodoru może łączyć dwie cząsteczki wiązaniem, które nazywamy wiązaniem protonowym lub wodorowym. Traktujemy je jako wiązanie jonowe silnie spolaryzowane, w którym czynnikiem polaryzującym atomy jest jądro wodoru. Często występuje w związkach organicznych i w strukturach krystalicznych kwasów nieorganicznych i wodorosoli. Najczęściej występuje ono między silnie elektroujemnymi atomami. Są dużo słabsze niż wiązania kowalencyjne i jonowe, lecz są silniejsze od wiązań Van der Vaalsa.

44. Ogólna charakterystyka jądra i jego skład: Atom składa się zasadniczo z dwóch części - z dodatnio naładowanego jądra oraz z zewnętrznej powłoki elektronowej. Jądra atomowe składają się z protonów i neutronów. Elektrony i pozytony nie istnieją w jądrze w jądrze jako cząstki trwałe, lecz powstają one w rezultacie przemian jądrowych. Średnica jądra atomowego, rzędu 10¹⁵ [m.], jest niewielka w porównaniu ze średnicą atomu ,ok.

10^-10 [m.]. Prawie cała masa atomu jest skupiona w małym jądrze otoczonym powłoką elektronową. Liczbę protonów wchodzących w skład jądra atomowego nazywamy liczbą atomową. Oznacza się ją symbolem Z. Liczby atomowe charakteryzują pierwiastki chemiczne. Liczbę masową, oznaczoną symbolem A, nazywamy sumę protonów i neutronów w jądrze. Budowę jądra dowolnego pierwiastka oznaczamy umieszczając przy jego symbolu liczby A i Z. Chcąc określić liczbę N neutronów w jądrze, należy od liczby masowej A odjąć atomową Z: N = A - Z.

45. Siły jądrowe: Siła wiążąca nukleon w jądrze musi być większa niż siła oddziaływania elektrostatycznego, aby przezwyciężyć odpychanie występujące między protonami. Na rysunku widać, że studnia potencjału opisująca to oddziaływanie jest o rząd wielkości głębsza niż energia potencjalna odpychania elektrostatycznego między dwoma protonami.

Linia przerywana odpowiada energii elektrostatycznej k_oe² / r. Wykres opowiada oddziaływaniu protonów, których spiny mają ten sam zwrot. Głębokość studni można wyznaczyć na podstawie energii wiązania deuteronu.

46. Efekt Comptona: Światło o energii E musi mieć pęd równy p = E / c. Kwant światła o energii E = hf musi mieć pęd p = hf / c. Jeśli zamiast f / c podstawimy 1 / λ, to otrzymamy:

p = h / λ. Pęd przekazywany kawałkowi metalu jest zbyt mały na to, by można było go zmierzyć. Natomiast jeśli foton zderzy się ze swobodnym elektronem, to przekazany elektronowi pęd powinien być mierzalny. Taki proces - rozproszenie fotonu na swobodnym elektronie - jest nazwany zjawiskiem Comptona. Długość fali rozproszonego fotonu wyrazimy za pomocą jego pierwotnej długości i kąta rozproszenia. W chwili początkowej mamy foton o pędzie p i energii pc, który zderza się z pozostającym w spoczynku elektronem o pędzie równym zeru i energii spoczynkowej równej mc². Po zderzeniu foton ma pęd p` skierowany pod kątem θ względem kierunku padania. Odrzucony elektron ma pęd p<sub>e</sub>` i całkowitą energię relatywistyczną F_e`. Zgodnie z zasadą zachowania energii, całkowita energia początkowa równa się całkowitej energii końcowej:

pc + mc² = p`c+ E<sub>e</sub>`,

(p - p` + mc)<sup>2</sup> = (E<sub>e</sub>` / c)², Zasada zachowania pędu daje: p - p` = p<sub>e</sub>`, Podnosząc obie strony do kwadratu otrzymujemy: p² - 2p ⋅ p` + p<sub>e</sub>` = p_e`

Ostatecznie otrzymujemy: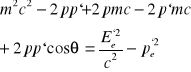

Prawą stronę możemy zastąpić wyrażeniem m²c²:

m²c² - 2pp`+2p`mc + 2pp`cosθ = m²c²

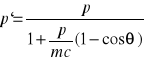
Podstawiając p = h / λ otrzymujemy:

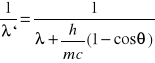
Jest to zjawisko Comptona.

47. Model kroplowy: Jest to model zaproponowany przez J. J. Thomsona, jest to model bezjądrowy. Atom jest kroplą dodatnio naładowanej elektrycznie cieczy, w której pływają ujemnie naładowane elektrony. Przypuśćmy, że atom jest kroplą naładowanej cieczy o promieniu R. Rozważmy cząstkę alfa, która trafiła w atom. Działają na nią siły elektryczne: przyciąganie ze strony elektronów oraz odpychanie ze strony atomowej „cieczy”. Na cząstkę alfa znajdującą się w odległości r od środka kropli działa tylko ta część całkowitego ładunku kropli, która zawarta jest wewnątrz kuli o promieniu r. Działanie różnych części warstwy kulistej o promieniu od r do R znoszą się nawzajem. Atomowa kropla powinna najsilniej rozpraszać cząstki przechodzące przy samym jej brzegu, a cząstki przebiegające przez jej środek w ogóle nie powinny zakrzywiać swych torów.

W rzeczywistości cząstka alfa rozproszeniu pod wszelkimi możliwymi kątami. Źródło sił rozpraszających jest skupione w bardzo niewielkim obszarze, w centrum atomu. Potrafimy wyliczyć wartość napięcia powierzchniowego. Im jądro jest bardziej sferyczne tym jest bardziej trwałe. Otrzymano w efekcie półempiryczny wzór na masę jądra: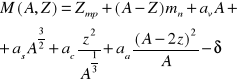
Pierwszy człon określa wartości wynikające ze składników, a drugi jest poprawką na wewnętrzne oddziaływanie między składnikami. a_v - poprawka objętościowa, proporcjonalna do A, miara średniej energii wiązania przypadającej na jeden nukleon, ≈ 16 MeV,

a_s - oddziaływanie powierzchniowe jest proporcjonalny do powierzchni jądra ( A ^{3 / 2} ), znak tej poprawki mówi nam o zmniejszaniu energii wiązania ze względu na oddziaływanie powierzchniowe, ≈ 18 MeV,

a_c - proporcjonalna do liczby protonów, związana jest z oddziaływaniem Kulombowskim. Zmniejsza energię wiązania. Ma duże znaczenie przy dużych jądrach.

≈ 0,7 MeV,

a_a - stabilność jądra. Człon asymetryczny. Uwzględnione są dane związane z ścieszką stabilności jądra. Gdy N > A poprawka się nie zeruje. ≈ 23 MeV, δ - ma różny zakres wartości (+pp, 0, np, pn, - nn). ≈ 11 A ^{- 1 / 2} wartość ta zależy od A, nie jest stała. Model ten nieprzewiduje oddziaływań kwantowych. Nie da się przewidzieć promieniowania γ, nie da się wytłumaczyć liczb magicznych. Wartość liczby A zapewniająca max. trwałość jądra: 2,8,20,50,82,126,184.

48. Model planetaerny: Czynnikiem rozpraszającym cząstki alfa jest bardzo małe tzw. jądro atomowe, obdarzone dodatnim ładunkiem elektrycznym, dokoła którego krążą elektrony. Im bliżej jądra przebiega cząstka alfa, tym silniej jest rozpraszana.

49. Model gazu Ferniego: Cząstki tworzące jądro są umieszczone w studni potencjału. Można opisać matematyczne zachowanie się elektronów w tej studni. Cząstki zgodnie z zakazem Pouliego mogą zajmować różne poziomy energetyczne. Mogę obliczyć energię wiązania i przewidzieć kolejne poziomy energetyczne. Równanie rozwiązuje się jako równanie Schrotingera: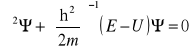
Sukcesem tego modelu są poziomy energetyczne, energia wiązania.

50. Model powłokowy jądra: Rozwiązujemy równanie Schrotingera dla jednego nukleonu w polu wytworzonym przez pozostałe nukleony i uwzględniamy własności spinu, oraz orbitalny moment pędu. Mogę przewidzieć istnienie poziomów energetycznych. Wewnątrz studni potencjału otrzymuję informacje o istnieniu powłok. Całkowicie wypełnione podpowłoki dają nam informacje zbieżne z liczbami magicznymi. Mogę przewidzieć max. stabilność jąder. Przewiduję też stan wzbudzony, wartość emitowanej energii.

51. Przekrój czynny i reakcje wywołane neutronami: Rozmiar , a stąd promień jądra atomowego można wyznaczyć bombardując neutronami o wysokiej energii płytkę wykonana z atomów. Neutron przechodzi przez płytkę po linii prostej, chyba że nastąpi bezpośrednie zderzenie z jądrem. Liczba neutronów ubywających z wiązki będzie proporcjonalna do powierzchni zajmowanej przez jądra. Prawdopodobieństwo ubywania neutronów jest dane ilorazem całkowitego obszaru zajmowanego przez jądra do rozmiaru płytki. Prawdopodobieństwo = N_a σ / A , gdzie N_a jest całkowitą liczbą atomów w płytce, σ - efektywną powierzchnią pojedynczego jądra,

A - powierzchnia płytki. Niech :

ϑ = N_a / A_x będzie liczbą atomów w jednostce objętości, a x - grubością płytki. Prawdopodobieństwo ubywania neutronów wynosi: ϑσdx dla płytki o grubości dx. Jeśli N jest liczbą neutronów w wiązce po przejściu drogi x, to zmiana N jest iloczynem tej liczby neutronów i prawdopodobieństwa ubywania: dN = - Nϑσdx,

dN / N = - ϑσdx, po scałkowaniu otrzymamy lnN = - ϑσdx + const. Przekrój czynny dany jest wzorem:

52. Rozszczepienie jąder atomowych: Energia wiązania na nukleon wzrasta z liczbą masową A do A ≈ 50. Zjawisko to można wyjaśnić jako wynik sumowania sił: wiązanie pojedynczego nukleonu jest tym silniejsze im więcej sąsiednich nukleonów go przyciąga. Przy większych odległościach między nukleonami dominują siły odpychania elektrostatycznego. Jeśli zbliżymy do siebie elektron i proton to wyzwoli się 13,6 eV energii, ponieważ masa atomu wodoru jest o 13,6 eV mniejsza niż suma mas swobodnego elektronu i protonu. Proces polegający na zbliżeniu dwóch lekkich jąder w wyniku czego uwolni się energia odpowiadająca różnicy mas nazywamy syntezą jądrową. Ciężkie jądra mają tendencje do rozszczepienia się na dwa mniejsze z wydzieleniem energii. Gdy rozdzielamy ciężkie jądro na dwie części, w powstałych grupach nukleonów następuje przegrupowanie i utworzone mniejsze jądra są silniej związane. Dzięki temu w procesie wydziela się energia. W zderzeniu z neutronami jądro uranu²³⁸ może zostać wzbudzone do stanu energetycznego leżącego w pobliżu szczytu bariery potencjału elektrostatycznego i wtedy prawdopodobieństwo rozszczepienia wyraźnie wzrasta. Jeden gram dowolnej substancji odpowiada energii mc² = 9 ⋅ 10¹³ [J]. Rozszczepienie jądrowe może w reakcji łańcuchowej stać się procesem samopodtrzymującym się. W każdej reakcji rozszczepienia powstają dwa lub trzy neutrony.

53. Masa krytyczna: Jeśli choć jednemu z neutronów powstających w reakcji łańcuchowej uda się wywołać rozszczepienie kolejnego jądra uranu to proces będzie się sam podtrzymywał. Ilość materiału, powyżej której jest spełniony powyższy warunek jest nazwany masą krytyczną.

54. Rozpad γ: Jeśli jądro jest wzbudzone do wyższego poziomu energetycznego, to może nastąpić samoczynna emisja fotonu i przejście do niższego poziomu energetycznego. Ponieważ odległość między poziomami energetycznymi w jądrach są rzędu MeV, więc fotony emitowane przez jądra będą miały energię setki tysiące razy większą niż fotony emitowane przez jądra nazywamy promieniami γ.

55. Rozpad β: Są to elektrony lub pozytony. W polu magnetycznym strumień promieni β uginają się silnie w tym kierunku, w którym odchylają się ujemne się ujemnie naładowane cząstki. Promienie β mają także własności jonizujące.

56. Promienie α: Odchylają się w polu magnetycznym w tę stronę, w którą odchylają się ładunki dodatni i maja własności jonizowania gazów.

57. Okres połowicznego rozpadu: Ilość substancji promieniotwórczej zmniejsza się w ten sposób, iż w jednakowych ściśle określonych odstępach czasu zanika połowa atomów pierwiastka. Charakterystyczny dla każdego pierwiastka promieniotwórczego czas, po którym następuje rozpad połowy jego atomów nazywa się okresem połowicznego rozpadu.

58. Zjawisko fotoelektryczne: Polega na emisji swobodnych elektronów z powierzchni naładowanej ujemnie płytki metalowej, pod wpływem promieniowania krótkofalowego. Energia kinetyczna emitowanych z powierzchni metalu elektronów nie zależy od natężenia promieniowania, ale wyłącznie od jego częstotliwości, a więc od długości fali. Według teorii kwantowej istota tego zjawiska polega na zderzeniu pojedynczego elementu promieniowania, czyli fotonu, ze swobodnym elektronem znajdującym się w metalu i wyrzuceniu go poza strefę przyciągania jonów.

59. Rodzaje widm: Ze względu na wygląd możemy podzielić na: widma emisyjne: obserwujemy je wtedy, gdy światło wysyłane przez ciało świecące trafia bezpośrednio do układu rozszczepiającego. Widmo nazywamy ciągłym wówczas gdy otrzymujemy wstęgę barwną, w której nie da się wyodrębnić poszczególnych linii odpowiadających danym długościom fali. Widmo pasmowe składają się z szeregu jasnych smug, posiadających wyraźne brzegi od strony krótkofalowej lub długofalowej. Widma liniowe składają się z oddzielnych, wyraźnych linii rozłożonych w sposób prawidłowy i tworzących serie widmowe. Widma takie dają pobudzone do świecenia gazy i pary jednoatomowe. Widma absorpcyjne: powstają wtedy, gdy na drodze światła pochodzącego ze źródła dającego widmo ciągle umieścimy ciało absorbujące o odpowiednio niższej temperaturze niż źródło światła. Linie absorpcyjne zajmują w widmie zawsze to samo miejsce co linie emisyjne. Przykładem widma absor. Są tzw. linie Fraunhofera w widmie światła słonecznego. Najsilniejsze z nich zostały oznaczone kolejnymi literami alfabetu zaznaczając od fal długich do krótkich.

59. Promieniowanie temperaturowe ciał: Jest to zjawisko przenoszenia ciepła na odległość , polegające na tym, że ciało pod wpływem swej temperatury zamienia energię cieplną na energię promieniowania, którą wysyła ze swej powierzchni. W jednakowych warunkach temperatury, ilość ciepła wypromieniowana przez jednostkę powierzchni ciała jest większa dla ciał o powierzchni czarnej i matowej.

60. Promienie Roentgena: Powstają wtedy gdy pędzące elektrony zostaną na swej drodze zahamowane przez szkło lub metal. Mają bardzo dużą częstotliwość , oraz własności: są niewidzialne dla oka, lecz oddziałują na kliszę fotograficzną, rozchodzą się prostoliniowo oraz podlegają interferencji i ugięciu, nie odchylają się w polu elektrycznym i magnetycznym, przenikają przez wiele materiałów nieprzezroczystych dla światła, są pochłaniane przez inne materiały.

1.Grawitacja

2.Elektromagnetyczne

3.Oddziaływanie silne

4.Jednorodność przestrzeni a zasada

zachowania pędu

5.Izotropowość przestrzeni a zasada zachowania momentu pędu

6.Nizmienniczość względem translacji

w czasie a zasada zachowania energii

7.Układy inercjalne, transformacja i

zasada względności Galileusza

8.Postulaty teorii względności

9.Transformacja Lorentza

10.Konsekwencja transformacji Lorentza. Dylatacja czasu

11.Skrócenie wymiarów podłużnych

12.Transformacja prędkości

13.Masa relatywistyczna, energia w

teorii względności

14.Związek między masą a energią

15.Oscylator harmoniczny, czas relaksacji.

16.Rodzaje fal, równanie fali płaskiej

i sferycznej

17.Interferencja fal

18.Fale stojące

19.Interferencja światła

20.Dyfrakcja

21.Polaryzacja światła

22.Pole elektryczne, prawo Gausa

23.Prawo Kulomba

24.Ruch cząsteczek naładowanych

w polu elektromagnetycznym:

25.Pole magnetyczne w próżni i w materii

, prawo Biota - Sawanta

26.Pole magnetyczne i jego względność

26.Pole magnetyczne i jego względność,

reguła prawej dłoni.

27.Równanie Maxwella

28.Paczki falowe

29 Zasada nieokreśloności Heisenberga

30. Równanie Schrodingera

31.Studnia potencjału

32.Funkcja falowa i jej interpretacja fizyczna

33.Atom wodoru

34.Liczby i stany kwantowe elektronów

35.Zakaz Pauliego

36.Laser

37. Model Bohra

38. Teoria pasmowa

39. Wiązania jonowe

40. Wiązania kowalencyjne

41. Wiązanie metaliczne

42. Wiązania Van deer Waalsa

43. Wiązania wodorowe

44. Ogólna charakterystyka jądra i jego

skład

45. Siły jądrowe

46. Efekt Comptona

47. Model kroplowy

48. Model planetaerny

49. Model gazu Ferniego

50. Model powłokowy jądra

51. Przekrój czynny i reakcje wywołane

neutronami

52. Rozszczepienie jąder atomowych

53. Masa krytyczna

54. Rozpad γ

55. Rozpad β

56. Promienie α

57. Okres połowicznego rozpadu

58. Zjawisko fotoelektryczne

59. Promieniowanie temperaturowe ciał

60. Promienie Roentge

---