ANALIZA STRUKTURY ZBIOROWOŚĆI
STRUKTURA - budowa wewnętrzna badanej zbiorowości statystycznej.
ROZKŁAD EMPIRYCZNY - przyporządkowanie liczby obserwacji (liczebności) odpowiednim wartościom cechy zmiennej.
Rozkład empiryczny prezentuje szereg rozdzielczy.
KLASY ROZKŁADÓW EMPIRYCZNYCH
Rozkłady symetryczne i asymetryczne
Rozkłady jednomodalne, bimodalne i wielomodalne
Rozkłady platokurtyczne (spłaszczone) i leptokurtyczne (wysmukłe)
ROZKŁAD SYMETRYCZNY - rozkład posiadający oś symetrii, obserwacje są rozłożone równomiernie po obu stronach osi symetrii. Oś symetrii przecina odciętą w punkcie, która jest średnią arytmetyczną zmiennej
r. normalny r. leptokurtyczny r. platokurtyczny
ROZKŁAD ASYMETRYCZNY - rozkład nie posiadający oś symetrii,
1. rozkład lewostronny - ujemny - większość jednostek grupuje się wokół wartości wyższych w szeregu;
2. rozkład prawostronny - dodatni - większość jednostek grupuje się wokół wartości niższych w szeregu;
r. prawostronny r. lewostronny r. skrajnie ujemny
r. skrajnie dodatni
ROZKŁAD JEDNOMODALNY - krzywa liczebności o jednym ekstremum (maksimum)
ROZKŁAD BIMODALNY - krzywa liczebności o dwóch ekstremach
ROZKŁAD WIELOMODALNY - krzywa liczebności ma więcej niż dwa maksima
r. jednomodalny r. bimodalny r. wielomodalny
PODSTAWOWE WSKAŹNIKI STRUKTURY I NATĘŻENIA
![]()
- bezwzględna liczba jednostek i-tego wariantu cechy
![]()
- łączna liczba jednostek w zbiorowości
![]()
- częstość tj. frakcja ![]()
![]()
- wskaźnik struktury, tj. stosunek wybranej części zbiorowości do całej zbiorowości; ![]()
![]()
- wskaźnik natężenia, tj. stosunek liczebności dwóch zbiorowości pozostających ze sobą w logicznej zależności
![]()
- liczebności szeregu skumulowanego, (sumowanie liczebności kolejnych przedziałów);
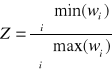
- względny wskaźnik podobieństwa struktur, tj. iloraz sumy mniejszych wskaźników zaobserwowanych w kolejnych przedziałach porównywalnych rozkładów i sumy większych wskaźników; ![]()
;
WŁASNOŚCI ROZKŁADU EMPIRYCZNEGO
TENDENCJA CENTRALNA - POŁOŻENIE - punkt skupienia obserwacji znajduje się w środku rozkładu (symetria) lub w pobliżu środka rozkładu (umiarkowana asymetria)
R. wykazujące tendencję centralną
R. nie wykazujące tendencji centralnej
DYSPERSJA - ZRÓŻNICOWANIE , ROZPROSZENIE, ZMIENNOŚĆ - zróżnicowanie jednostek zbiorowości między sobą wartościami cechy zmiennej
R. słabo zróżnicowane
R. umiarkowanie zróżnicowane
R. silnie zróżnicowane
ASYMETRIA - SKOŚNOŚĆ - sposób rozmieszczenia liczebności przy wartościach cechy
R. symetryczne
R. umiarkowanie asymetryczne (p,l)
R. skrajnie asymetryczne (p,l)
KONCENTRACJA - KURTOZA, SPŁASZCZENIE - stopień skupienia obserwacji wokół wartości średniej arytmetycznej
R. normalny
R. wysmukły
R. spłaszczony
PARAMETRY OPISUJĄCE WŁASNOŚCI ROZKŁADU
PARAMETRY KLASYCZNE - miary obliczane na podstawie wszystkich obserwacji, stosowane do analizy rozkładów charakteryzujących się te tendencją centralną;
PARAMETRY POZYCYJNE - wyznaczane na podstawie miejsca jakie zajmują w szeregu lub częstotliwości występowania; szczególnie przydatne w analizie szeregów silnie (skrajnie) asymetrycznych, szeregów z otwartymi przedziałami klasowymi,
WŁASNOŚĆ ROZKŁADU |
MIARY KLASYCZNE |
MIARY POZYCYJNE |
TENDENCJA CENTRALNA |
Średnia arytmetyczna |
Mediana Me Dominanta D Kwartyle Q1,, Q3 Decyle D1, D2, ..., D9 |
DYSPERSJA |
Wariancja s2 Odchylenie przeciętne d Odchylenia standardowe s Współczynnik zmienności V(s) |
Rozstęp R Odchylenie ćwiartkowe Q Współczynnik zmienności V(Q) |
ASYMETRIA |
Moment trzeci centralny
Moment trzeci względny |
Współczynnik skośności A(x) |
KONCENTRACJA |
Moment czwarty centralny
Moment czwarty względny |
Wskaźnik spłaszczenia Wk |
MIARY POŁOŻENIA
ŚREDNIA ARYTMETYCZNA - iloraz globalnej wartości cechy oraz liczby obserwacji. Wskazuje jaki poziom badanej cechy przypada na jednostkę zbiorowości; określa jaki jest przeciętny (średni) poziom badanej cechy w zbiorowości.
szereg szczegółowy:
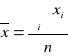
szereg rozdzielczy jednostopniowy:
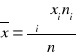
szereg rozdzielczy wielostopniowy:
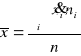
WŁASNOŚCI ŚREDNIEJ ARYTMETYCZNEJ
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
MEDIANA - wartość środkowa; wartość cechy jaką posiada jednostka znajdująca się w środku uporządkowanego szeregu. Oznacza ona, iż połowa zbiorowości ma wartości cechy nie większe niż mediana, a druga połowa wartości nie mniejsze niż mediana.
szereg szczegółowy - porządkujemy obserwacje wg rosnących wartości cechy i wskazujemy obserwację środkową.
W przypadku parzystej liczby obserwacji wartość mediany jest średnią arytmetyczną z dwóch środkowych obserwacji.
np.
2 3 3 6 7 7 9 11 13
![]()
11 13 13 16 18 19 22 22 25 30
![]()
szereg rozdzielczy jednostopniowy - 1) wyznaczamy numer jednostki znajdującej się w szeregu, tzw. pozycję mediany, 2) w szeregu skumulowanym znajdujemy klasę zawierającą pozycję mediany, 3) wartość mediany jest wartością cechy we wskazanej klasie;
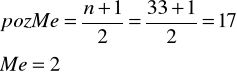
![]()
xi |
ni |
nicum |
0 |
6 |
6 |
1 |
7 |
13 |
2 |
11 |
24 |
3 |
4 |
28 |
4 |
3 |
31 |
5 |
2 |
33 |
∑ |
33 |
x |
szereg rozdzielczy wielostopniowy - 1) wyznaczamy numer jednostki znajdującej się w szeregu, tzw. pozycję mediany, 2) w szeregu skumulowanym znajdujemy klasę zawierającą pozycję mediany, 3) wyznaczamy medianę w oparciu o wzór interpolacyjny:
![]()
|
ni |
nicum |
0-10 |
9 |
9 |
10-20 |
19 |
28 |
20-30 |
23 |
51 |
30-40 |
14 |
65 |
40-50 |
9 |
74 |
50 i więcej |
7 |
81 |
∑ |
81 |
x |
![]()
![]()
KWARTYLE - wartości ćwiartkowe, dzielą zbiorowość, uporządkowaną wg rosnących wartości badanej cechy, na cztery jednakowo liczne części.
KWARTYL PIERWSZY Q1 - oznacza, iż 25% badanej zbiorowości osiąga wartości cechy nie większe niż Q1, a 75% zbiorowości ma wartości cechy nie mniejsze niż Q1.
KWARTYL DRUGI Q2 - jest równy Medianie, gdyż oznacza, iż 50% badanej zbiorowości osiąga wartości cechy nie większe niż Q2, a druga połowa - wartości nie mniejsze niż Q2.
KWARTYL TRZECI Q3 - oznacza, iż 75% badanej zbiorowości osiąga wartości cechy nie większe niż Q3, zaś pozostałe 25% - wartości nie mniejsze niż Q3.
szereg szczegółowy - porządkujemy obserwacje wg rosnących wartości cechy i wskazujemy obserwację leżącą w ¼ zbiorowości.
np.
2 3 3 6 7 7 9 11 13
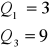
szereg rozdzielczy jednostopniowy - 1) wyznaczamy numer jednostki znajdującej się w szeregu, tzw. pozycję mediany, 2) w szeregu skumulowanym znajdujemy klasę zawierającą pozycję mediany, 3) wartość mediany jest wartością cechy we wskazanej klasie;
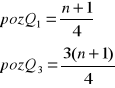
xi |
ni |
nicum |
0 |
6 |
6 |
1 |
7 |
13 |
2 |
11 |
24 |
3 |
4 |
28 |
4 |
3 |
31 |
5 |
2 |
33 |
∑ |
33 |
x |
Q1
Q3
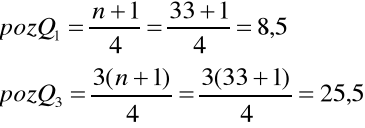
szereg rozdzielczy wielostopniowy - 1) wyznaczamy numer jednostki znajdującej się w szeregu, tzw. pozycję, 2) w szeregu skumulowanym znajdujemy klasę zawierającą pozycję parametru, 3) wyznaczamy parametr w oparciu o wzór interpolacyjny:
![]()
|
ni |
nicum |
0-10 |
9 |
9 |
10-20 |
19 |
28 |
20-30 |
23 |
51 |
30-40 |
14 |
65 |
40-50 |
9 |
74 |
50 i więcej |
7 |
81 |
∑ |
81 |
x |
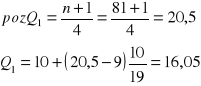
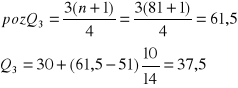
DOMINANTA - MODA - to pozycyjna miara położenia wyznaczana przez częstotliwość występowania wyróżnionych wartości cechy. Informuje ona jaka wartość cechy występuje najczęściej (dominuje).
szereg szczegółowy - porządkujemy obserwacje wg rosnących wartości cechy i wskazujemy obserwację występującą najczęściej.
np.
2 3 3 6 7 7 7 9 11 13
![]()
szereg rozdzielczy jednostopniowy - wskazujemy wartość cechy wokół oscyluje największa liczba obserwacji
xi |
ni |
0 |
6 |
1 |
7 |
2 |
11 |
3 |
4 |
4 |
3 |
5 |
2 |
∑ |
33 |
![]()
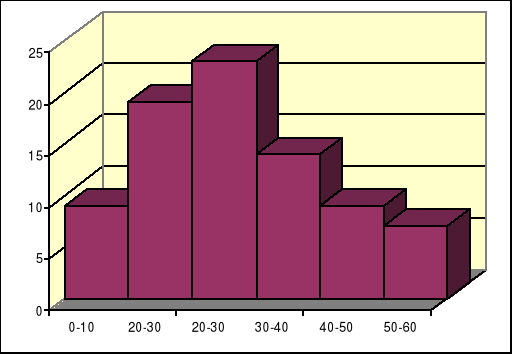
szereg rozdzielczy wielostopniowy - 1) wskazujemy przedział klasowy, w którym skupia się największa liczba obserwacji 2) wyznaczamy dominantę w oparciu o wzór interpolacyjny:
![]()
|
ni |
0-10 |
9 |
10-20 |
19 |
20-30 |
23 |
30-40 |
14 |
40-50 |
9 |
50-60 |
7 |
∑ |
81 |
![]()
GRAFICZNE WYZNACZANIE DOMINANTY
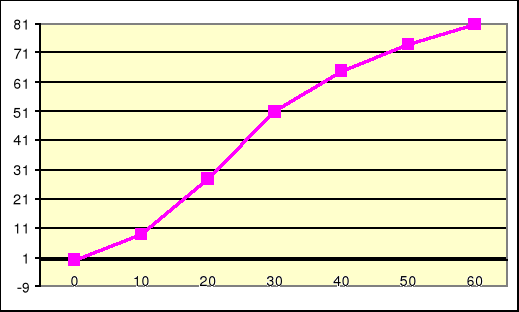
GRAFICZNE WYZNACZANIE KWARTYLI
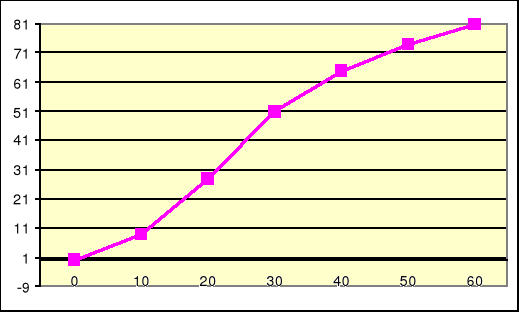
12
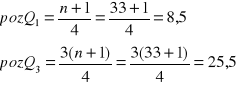
![]()
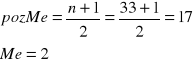
Wyszukiwarka
Podobne podstrony:
489
489
489
489 Polska reklama 7151 874 4
489
489
489
489
489
489
KSH, ART 161 KSH, II CSK 489/08 - postanowienie z dnia 25 lutego 2009 r
489
Jung Archetypy i symbole s 489 496
489
489
489
więcej podobnych podstron