STATYSTYKA
12-02-2001
Statystyka - (łac. status - `państwo') - nauka traktująca o metodach ilościowych badania prawidłowości zjawisk masowych
metoda - swoisty sposób badania liczbowego specjalnego typu zbiorowości
zjawiska masowe - takie zjawiska, które badane w dużej masie zdarzeń wykazują prawidłowości, których nie można zaobserwować w pojedynczym przypadku (np. zgony)
Każde zjawisko kształtuje się pod wpływem dwojakiego rodzaju przyczyn:
głównych - działają na każde zjawisko w sposób jednakowy
mają charakter wewnętrzny
działają w ściśle określonym kierunku
są wspólne dla wszystkich jednostek zbiorowości statystycznej
powodują prawidłowości w procesach masowych
ubocznych (indywidualnych, nietypowych)
działają na każde zjawisko w sposób odmienny
źródłem ich powstania są czynniki zewnętrzne (stąd nazwa: przyczyny przypadkowe)
powodują odchylenia od procesów masowych
Wszystkie zjawiska masowe odznaczają się pewnymi prawidłowościami - zadaniem statystyki jest poznanie tych prawidłowości i ich wyrażenie ilościowe.
Prawidłowości występujące wyłącznie w procesach masowych (tj. w zbiorowości o dużej liczbie jednostek) nazywamy prawidłowościami statystycznymi.
U podstaw badania prawidłowości statystycznych leży prawo wielkich liczb - matematyczne sformułowanie pewnych prawidłowości występujących w zjawiskach masowych:
Określenie prawidłowości wymaga aby obserwowane zbiorowości jednostek były dostatecznie liczne: im większa liczebność, tym większa szansa, że ujawni się efekt działania przyczyn głównych.
W indywidualnych przypadkach działanie przyczyn ubocznych zaciemnia działanie przyczyn głównych, natomiast w dużej masie działanie przyczyn ubocznych znosi się w mniejszym lub większym stopniu i występuje wyraźne działanie prawa wielkich liczb.
W statystyce każda wielkość ma sens wtedy i tylko wtedy gdy ma odpowiednik w rzeczywistości.
Statystyka - to nauka formalna - ma znaczenie użytkowe.
Teoria statystyki - zajmuje się tym, w jaki sposób i za pomocą jakich metod poznawać rzeczywistość - jakimi metodami badać prawidłowości i jak je interpretować.
Metoda poznawania zjawisk masowych to metoda indukcyjna - umożliwia uogólnienie wyników otrzymanych z badania jednostek na całą zbiorowość. Taką generalizację nazywamy wnioskowaniem statystycznym, a ten rodzaj badań wymaga zastosowania metod statystyki matematycznej.
Zadania statystyki:
idiograficzne - mają charakter opisowy, wiążący się z konstrukcją metod umożliwiających opis otaczającej nas rzeczywistości
eksplikacyjne - pozwalają na streszczenie wyników opisu zjawisk w syntetycznej formie, a tym samym dają podstawy do wnioskowania
Subdyscypliny przedmiotowe statystyki:
statystyka ludności
statystyka ekonomiczna
statystyka społeczna
statystyka ubezpieczeń
statystyka handlu
statystyka rolnictwa
statystyczna kontrola jakości
Historia
Starożytność (Egipt, Grecja, Rzym, Chiny)
sporządzano spisy ludności i majątku, które dostarczały danych charakteryzujących stosunki społeczno gospodarcze
cenzusy i spisy przeprowadzano w Rzymie w odstępach pięcioletnich (charakter militarny i podatkowy)
Średniowiecze
obserwacje o znamionach statystyki prowadziły instytucje kościelne oraz feudałowie, przy czym miały one charakter prywatno-gospodarczy
1086r. - Księga Sądu Ostatecznego - ewidencja przeprowadzona w Anglii, zawierająca opis posiadłości króla i kleru, z określeniem obszaru i wartości
XIII wiek
w północnych Włoszech (głównie w Wenecji) pozyskiwano materiały statystyczne do oceny aktualnej oraz przewidywanej przyszłej sytuacji
XVII wiek
rzeczywisty rozwój statystyki jako nauki rozpoczyna się od momentu zaobserwowania prawidłowości w zjawiskach masowych
J. Grant (1620-1679) - badając księgi stanu cywilnego ludności Londynu wykrył prawidłowości występujące w zgonach → „tablice trwania życia”
W. Petty (1625-1687) - opublikował pracę „Arytmetyka polityczna”, w której mówi się o nowej nauce umożliwiającej identyfikację prawidłowości w zjawiskach masowych
J. Grant i W. Petty uważani są za pierwszych statystyków i nazywani byli arytmetykami politycznymi
XVIII wiek
G. Achenwall (1719-1772) - prof. w Marburgu, później w Getyndze, po raz pierwszy użył słowa statystyka; pod pojęciem tym rozumiał zbiór wiadomości o państwie
pojawił się drugi bardzo ważny nurt badań naukowych dotyczących nowego działu matematyki - rachunek prawdopodobieństwa
rozwija się w oparciu o badania zjawisk występujących w grach losowych - gracze w kości i karty, chcąc dociec w jaki sposób osiągnąć wielką wygraną czynili ogromną ilość obserwacji a rezultatem było powstanie teorii prawdopodobieństwa
do przedstawicieli tego kierunku należą:
Galton Kołmogorow
Pearson Lange
Queletet Markow
Gauss Neyman-Spława
19-02-2001
Pojęcie statystyka odnoszone jest do:
nauki traktującej o metodach ilościowych badania prawidłowości zjawisk (procesów) masowych - statystyka opisowa (zajmuje się zagadnieniami związanymi z gromadzeniem i prezentacją danych oraz badaniem populacji na podst. pobranych prób);
oznaczania określonych charakterystyk opisowych (parametrów) obliczonych ze zbiorowości próbnych (średnia arytmetyczna, odchylenie standardowe) - statystyka matematyczna (zwana też wnioskowaniem statystycznym - zajmuje się metodami wnioskowania o całej zbiorowości generalnej na podst. zbadania pewnej jej części, wybranej w sposób losowy, zwanej próbą opartą na metodach rachunku prawdopodobieństwa).
Przedmiotem badania statystycznego jest zbiorowość statystyczna (masa statystyczna, populacja).
Zbiorowość statystyczna - odpowiednio liczny zbiór elementów nieidentycznych, ale tworzących całość jednoznacznie określoną pod względem rzeczowym, czasowym i przestrzennym
Podział zbiorowości statystycznych:
z punktu widzenia liczebności:
skończenie liczne - zbiorowości składające się z określonej przeliczalnej liczby elementów (np. zbiór studentów AE Poznań 2000/2001)
nieskończenie liczne - zbiorowości tworzone przez elementy o nieprzeliczalnej liczbie (np. zbiór organizmów żywych na Ziemi)
z punktu widzenia czasu:
statyczne - zbiorowości tworzone przez jednostki, które istniały, istnieją lub będą istnieć w określonym momencie czasu (np. ludność Polski stan na 31.XII.2000)
dynamiczne - zbiorowości, które tworzą jednostki obserwowane w pewnym przedziale czasu (np. kredyty konsumenckie w PKO BP S.A. od stycznia do grudnia 2000r.)
z punktu widzenia treści:
jednorodna - zbiorowość, którą tworzą jednostki niezróżnicowane pod względem cechy stałej (np. studenci AE Poznań 2000/2001)
niejednorodna - zbiorowość, w której jednostki nie posiadają takiej samej cechy przedmiotowej (np. studenci i pracownicy AE - w jednym zbiorze)
z punktu widzenia pełnej lub częściowej obserwacji jednostek:
generalna - zbiorowość wszystkich elementów, liczebność takiej zbiorowości może być skończona lub nieskończona, zbiorowość może być statyczna lub dynamiczna
próbna - część zbiorowości wybrana losowo lub przez wybór celowy:
n - liczebność danej próby
n ≤ 30 - próba mała
n > 30 - próba duża
Jednostka statystyczna - poszczególny element wchodzący w skład zbiorowości statystycznej; jednostki statystyczne muszą być jednoznacznie określone pod względem rzeczowym, czasowym i przestrzennym.
Podział jednostek statystycznych:
jednostka prosta - taka, której elementy nie tworzą zbiorowości statystycznej; (np. istoty żyjące, zdarzenia typu wypadek drogowy)
jednostka złożona (agregatowa) - taka, której elementy mogą tworzyć dalsze zbiorowości (np. województwo - dzieli się na powiaty)
Suma jednostek statystycznych - określana jest jako liczebność zbiorowości i oznaczana symbolem N.
ni - jednostki zbiorowości (i = 1, 2, ..., k)
![]()
Cechy statystyczne - właściwości, którymi odznaczają się jednostki wchodzące w skład badanej zbiorowości statystycznej
cechy statystyczne
stałe zmienne
rzeczowe czasowe przestrzenne rzeczowe czasowe przestrzenne
ilościowe jakościowe
ciągłe skokowe
Cechy stałe
wspólne dla wszystkich jednostek zbiorowości
służą do zdefiniowania zbiorowości pod względem rzeczowym (co?), czasowym (kiedy?), przestrzennym (gdzie?)
pozwalają odgraniczyć badaną zbiorowość i wchodzące w jej skład jednostki od innych zbiorowości
nie stanowią one przedmiotu badań statystycznych
np. w zbiorowości ludności Polski - cecha stała: posiadanie obywatelstwa polskiego
Cechy zmienne - właściwości, którymi poszczególne jednostki zbiorowości różnią się między sobą; podlegają one badaniu statystycznemu:
rzeczowe (przedmiotowe) - służą do określenia kogo lub co badamy (właściwości, którymi charakteryzują się ściśle określone zbiory osób, rzeczy lub zjawisk)
jakościowe (niemierzalne) - nie da się ich wyrazić liczbowo, ale można je opisać słownie (np. płeć, pochodzenie społeczne, rodzaj kredytu) - rodzaj właściwości, której konkretny wariant występuje lub nie u danej jednostki
ilościowe (mierzalne) - można je wyrazić w jednostkach miar (właściwość występująca z określonym liczbowo natężeniem u wszystkich jednostek zbiorowości)
ciągłe - takie, które mogą przyjmować dowolne wartości z określonego przedziału liczbowego (np. wiek, wynagrodzenie, staż pracy, wzrost)
skokowe - takie, które przyjmują wartości równe liczbom naturalnym (np. liczba dzieci w rodzinie, liczba pracowników)
czasowe - określają, jakiego okresu lub momentu obserwacja dotyczy
przestrzenne - określają lokalizację danego zjawiska w określonym miejscu (rozmieszczenie danego zjawiska w przestrzeni)
Podział cech na stałe i zmienne jest względny - uzależniony od przedmiotu i rodzaju badania (np. płeć w zbiorowości ludności Polski jest cechą zmienną, a w zbiorowości kobiet w Polsce - cechą stałą).
Wariant cechy - to odmiana cechy:
warianty cechy ilościowej - to rezultaty pomiaru jednostki
warianty cechy jakościowej - identyfikujemy wg opisu uwzględniającego wszystkie odmiany cech
Przykład
Zbiorowość |
Jednostka |
Cechy zmienne |
Wariant cechy |
Rodzaj cechy |
Studenci I roku WE, AE Poznań w roku akadem. 2000/2001 |
Student I roku WE, AE Poznań w roku akadem. 2000/2001 |
płeć |
kobieta, mężczyzna |
rzeczowa jakościowa |
|
|
wzrost |
158,160,168... |
rzeczowa ilościowa ciągła |
|
|
wiek |
19,20,... |
rzeczowa ilościowa ciągła |
|
|
pochodzenie |
robotnicze, chłopskie.. |
rzeczowa jakościowa |
|
|
miejsce zam. |
Poznań,Piła,Gniezno... |
przestrzenna |
|
|
średnia ocen z I semestru |
3.0, 3.21, ... |
rzeczowa ilościowa ciągła |
|
|
liczba rodzeństwa |
1,2,3... |
rzeczowa ilościowa skokowa |
|
|
... |
|
|
Zasady wyodrębniania zbiorowości statystycznej:
Zbiorowością statystyczną może być każdy wybrany przedmiot badania, wszelka masa osób, przedmiotów lub zdarzeń, jeśli potrafimy wyodrębnić w sposób jednoznaczny jednostki i jeżeli spełnione zostaną w stosunku do tych jednostek następujące warunki:
masowość badania - warunek wywodzi się z rachunku prawdopodobieństwa,
posiadanie cech stałych i zmiennych (co najmniej 1 cechy stałej i 1 cechy zmiennej),
jednorodność zbiorowości.
Etapy badania statystycznego
Badanie statystyczne - proces złożony, obejmujący całokształt czynności prowadzących do odkrycia prawidłowości statystycznych
Etapy badania statystycznego:
przygotowanie badania
obserwacja statystyczna
opracowanie i prezentacja materiału statystycznego
analiza opracowanego materiału statystycznego
Etapy te są ze sobą nierozerwalnie związane i stanowią logiczną całość.
W obrębie poszczególnych etapów badania możliwe jest zastosowanie różnych metod statystycznych, których każdorazowy wybór zależy d rodzaju materiału statystycznego oraz od celu badania.
Etap I - przygotowanie badania.
Etap ten obejmuje czynności przygotowujące takie jak:
ustalenie celu i zakresu badania
określenie zbiorowości statystycznej i cech podlegających badaniu
zdefiniowanie jednostek statystycznych
dokonanie wyboru metody badania
Etap II - obserwacja statystyczna.
Obserwacja statystyczna - ustalenie i rejestrowanie ogółu faktów dotyczących jednostek statystycznych
Materiał statystyczny - zbiór informacji, ustalony z reguły na piśmie, o wchodzących w skład badanej zbiorowości jednostkach i charakteryzujących je cechach:
materiał pierwotny - to materiał gromadzony w toku specjalnych badań statystycznych (np. informacje utrwalone na arkuszach spisowych); jest to materiał lepszy - dokładniejszy, bardziej wiarygodny, ale i kosztowny i pracochłonny w uzyskaniu
materiał wtórny - to materiał zebrany dla celów innych niż statystyczne (np. do celów podatkowych, księgowych); materiał nie tak kosztowny, ale wadą możliwość obarczenia błędami
Formularz (kwestionariusz) statystyczny - podstawowe narzędzie przy zbieraniu pierwotnego materiału statystycznego - to zbiór pytań dotyczących pewnego zagadnienia i uszeregowanych logicznie.
Zasady opracowywania kwestionariuszy:
możliwie mało pytań w kwestionariuszu - należy uwzględnić tylko pytania niezbędne dla oceny badanej zbiorowości; zbyt duża liczba pytań powoduje, że odpowiedzi na część pytań mogą być udzielane bez zastanowienia
pytania sformułowane zwięźle, krótko, a jednocześnie jasno - stopień trudności może być różny, z zależności od tego, kto wypełnia formularz
pytania należy sformułować tak, aby w miarę możliwości uzyskać odpowiedzi wyrażane w liczbach lub słownie: tak/nie
w miarę możności należy unikać pytań drażliwych i wymagających odpowiedzi poufnych
pytania należy uszeregować wg kolejności logicznej ułatwiającej zrozumienie celu badania
ważna jest forma zewnętrzna formularza, druk musi być czytelny
kwestionariusz powinien zawierać krótką instrukcję o sposobie jego wypełniania; jeżeli objaśnienia są krótkie, umieszcza się je bezpośrednio przy pytaniu.
Budowa kwestionariusza:
I - nazwa instytucji, cel badania, itp.
II - część właściwa - pytania
III - uwagi dotyczące wypełniania kwestionariusza
Podział badań statystycznych:
Badania całkowite:
spis statystyczny
rejestracja bieżąca
bieżąca sprawozdawczość statystyczna
Badania częściowe:
metoda ankietowa
metoda monograficzna
metoda reprezentacyjna
ad. a.) Badania całkowite - obejmują wszystkie jednostki badanej zbiorowości; mogą być ciągłe, periodyczne lub doraźne.
Spis statystyczny - metoda gromadzenia danych w pewnych dłuższych odstępach czasu;
może to być badanie jednorazowe lub periodyczne
celem spisu jest ustalenie wielkości i struktury badanego zjawiska
biuro statystyczne ONZ zaleca, aby spisy ludności były przeprowadzane w latach kończących się na zero lub liczby bliskie zeru
wg biura ONZ spis powinien zawierać tzw. minimum merytoryczne - dla krajów europejskich 19 pytań poruszających zagadnienia: demograficzne (płeć, wiek, stan cywilny, obywatelstwo, itp.), ekonomiczne (np. zawód), społeczne, geograficzne (np. miejsce zamieszkania i jego charakter); może zawierać także pytania dodatkowe (np. ustalające dzietność rodzin, migracje ludności)
cechy podstawowe spisu:
centralizacja - spis przeprowadza rząd kraju, którego mieszkańcy zostaną spisani, rząd wyznacza odpowiednie organy do realizacji spisu i opracowania zebranego materiału
powszechność
imienność
jednoczesność
regularność i międzynarodowa porównywalność
statystyczne ujęcie wyników i zapewnienie tajemnicy statystycznej
mikrospisy - sporządzane o metodę reprezentacyjną (badanie częściowe), np. spisy gospodarstw rolnych, majątków trwałych; w Polsce:1974, 1984, 1995
historia:
starożytność - cenzusy (ostatni w Rzymie w 48r. n.e. - objął ok. 6 mln ludności)
w USA: pierwszy spis (imienny, bezpośredni) w 1790r., później w odstępach 10-letnich; w 1890r. przeprowadzono spis zawierający 13 tys. pytań (w tym 5 tys. dotyczyło ubezpieczeń), którego publikacja zajęła 24 tys. stron (koszt - $11mln)
w Polsce: pierwszy spis w 1789r., kolejne: 1808, 1811, 1921, 1931, 1950, 1960, 1970, 1978, 1988; najbliższy w 2002r.
Rejestracja bieżąca - polega na ciągłym notowaniu określonych faktów
różni się od spisu tym, że nie jest to badanie jednorazowe, lecz ciągłe, wykonywane stale
np. ewidencja ludności w urzędach stanu cywilnego
Bieżąca sprawozdawczość statystyczna
to sprawozdania wykonywane na jednolitych formularzach przez poszczególne podmioty gospodarcze
sprawozdania te są przekazywane do Wojewódzkich Urzędów Statystycznych, a stamtąd do GUS-u
26-02-2001
ad. b.) Badania częściowe - obejmują jedynie część jednostek badanej zbiorowości, na podstawie wyników z próby oceniamy całą zbiorowość.
Metoda ankietowa - jest jednym z najszybszych sposobów badania zjawisk masowych
stosujemy ją zawsze w celu wyświetlenia jakiegoś specyficznego, ściśle określonego zjawiska
badanie ankietowe sprowadza się do udzielenia odpowiedzi na pytania ujęte w kwestionariuszu
ankieta ≠ kwestionariusz (formularz)
jest jedną z metod badania częściowego
jest zbiorem pytań - stosujemy go zarówno w badaniu całkowitym, jak i w częściowym
badanie ankietowe jest badaniem dobrowolnym
jest powszechnie stosowaną metodą badania opinii publicznej na temat aktualnych zagadnień społecznych, politycznych, gospodarczych
podstawową zaletą metody ankietowej jest szybkość uzyskania informacji i zdecydowanie mniejsze koszty w porównaniu do kosztów badania całkowitego
badanie ankietowe nie jest w pełni badaniem reprezentacyjnym - należy ostrożnie formułować wnioski i podejmować decyzje
Metoda monograficzna - jest to jedna z najstarszych metod badań społeczno-gospodarczych
polega ona na badaniu indywidualnego przypadku (tj. pojedynczej jednostki statystycznej), np. na badaniu jednej wsi, powiatu, miasta, województwa
z uwagi na fakt, że monografia dotyczy jednego przypadku, porusza bardzo dużą ilość problemów - pozwala zatem na gruntowną i wnikliwą analizę danego przykładu i pogłębia naszą wiedzę o badanej zbiorowości
badania monograficzne zyskały znacznie szersze zastosowanie pod koniec XIXw. (do uzyskiwania obrazu warunków życia ludności)
Metoda reprezentacyjna - polega na tym, że ze zbiorowości badanej (zwanej populacją generalną) losujemy jednostki (czyli pobieramy próbę) i na podstawie zbadanej próby wnioskujemy o całej zbiorowości
jednostki statystyczne do próby mogą być wybrane dwoma sposobami:
wybór przez losowanie - czyli wybór przypadkowy dający takie same szanse do wylosowania (każda jednostka ma takie same szanse znalezienia się w próbie)
celowa selekcja - w tym przypadku w sposób świadomy (tj. oparty na wstępnym rozpoznaniu zagadnienia) typuje się pewne jednostki do próby
należy zawsze dokonać oceny reprezentacyjności próby (oblicza się niezbędną liczebność próby przed przeprowadzeniem badania i po jego przeprowadzeniu)
w przypadku metody reprezentacyjnej uzyskane wyniki uogólnia się na całą zbiorowość (np. mikrospisy)
metoda reprezentacyjna ma zastosowanie w badaniu zagadnień społeczno-ekonomicznych
Etap III - opracowanie zebranego materiału statystycznego.
kontrola materiału statystycznego
grupowanie materiału statystycznego
zliczanie materiału statystycznego
budowa szeregów statystycznych
sporządzanie tablic statystycznych
sporządzanie wykresów statystycznych
ad. a.) Kontrola materiału statystycznego:
Każdy zebrany materiał statystyczny (pierwotny czy wtórny) musi być poddany kontroli - od kontroli zależy bowiem w dużej mierze poprawność wniosków formułowanych na podstawie informacji uzyskiwanych z badaniach.
W materiale statystycznym mogą występować różnego rodzaju błędy lub braki. Błędy w materiale mogą być niezamierzone albo umyślne - wśród błędów niezamierzonych można wyróżnić:
błędy systematyczne - przyczyną ich powstawania jest przede wszystkim wieloznaczność pojęć badanej cechy oraz niedokładność definicji,
błędy przypadkowe - powstają na skutek szeregu różnych drobnych przyczyn, a najczęściej na skutek nieuwagi.
Kontrola materiału statystycznego dotyczy dwóch zagadnień:
kompletność materiału statystycznego - kontrola kompletności polega na stwierdzeniu czy zebrano formularze od wszystkich jednostek oraz czy wszystkie pozycje formularza są wypełnione,
jakość materiału statystycznego - kontrola jakościowa wymaga starannego przejrzenia każdego wypełnionego kwestionariusza; polega ona na badaniu zgodności, logiczności oraz wiarygodności odpowiedzi.
ad. b.) Grupowanie materiału statystycznego:
Zebrany materiał jest materiałem nieuporządkowanym (surowym) - czynność porządkowania takiego materiału nosi nazwę grupowania statystycznego.
Grupowanie materiału statystycznego - polega na mniej lub bardziej zróżnicowanym podziale niejednorodnej zbiorowości na możliwie jednorodne grupy według wybranych kryteriów.
Dopiero w ramach poszczególnych grup możliwe jest dokonanie szczegółowych obliczeń (grupowanie stanowi podstawę umożliwiającą obliczenie charakterystyk liczbowych).
Grupowanie statystyczne pozwala na prawidłowe odzwierciedlenie struktury badanej zbiorowości oraz ustalenie związków między badanymi cechami.
Warunki dotyczące poprawności przeprowadzenia grupowania:
dokładnie i konkretnie musi być sformułowany cel badania,
zjawiska muszą być ujęte w ich wzajemnym powiązaniu,
za podstawę grupowania należy przyjąć cechy istotne dla badanej zbiorowości.
W zależności od celu badania wyróżniamy trzy rodzaje grupowania statystycznego:
grupowanie typologiczne (dawniej nazywane „grupowaniem leninowskim”) - polega na podziale zbiorowości na jakościowo jednorodne grupy (np. podział przedsiębiorstw na małe, średnie, duże)
grupowanie wariancyjne - najczęściej stosowane; polega ono na łączeniu poszczególnych jednostek wg wielkości pewnej interesującej nas cechy;
celem tego grupowania jest uporządkowanie badanej zbiorowości i poznanie jej struktury
przy tym grupowaniu mamy zawsze do czynienia z jedną cechą mierzalną (ilościową)
np. grupowanie studentów wg liczby punktów uzyskanych na egzaminie
grupowanie analityczne - polega na podziale zbiorowości w oparciu o co najmniej dwie cechy
pozwala ono na ustalenie współzależności między badanymi cechami
z tym rodzajem grupowania mamy do czynienia np. w rachunku korelacji
Efektem grupowania statystycznego są szeregi statystyczne.
ad. c.) Zliczanie materiału statystycznego:
Występują tutaj cztery metody:
Metoda bezpośrednia - polega na tym, że przeglądamy zebrany materiał statystyczny i zliczamy jednostki należące do określonej grupy (metoda przestarzała).
Metoda kreskowa - polega na tym, że przeglądamy materiał statystyczny i każdą jednostkę zaliczamy do określonej grupy przez narysowanie kreski.
Metoda kartkowa - stosowana jest wówczas, gdy materiał statystyczny znajduje się na indywidualnych formularzach; przeglądając poszczególne kartki odkładamy każdą z nich na odpowiednie stanowiska w zależności od tego, do jakiej grupy należą.
Metoda maszynowa - zliczanie przy pomocy komputerów; najczęściej stosowana.
ad. d.) Budowa szeregów statystycznych:
Szereg statystyczny - ciąg wielkości statystycznych rosnących lub malejących, uporządkowanych wg określonych cech (inaczej mówiąc szereg statystyczny to ciąg liczbowy monotoniczny, ograniczony z góry lub z dołu).
Podział szeregów statystycznych:
szeregi
z punktu widzenia budowy (formy) z punktu widzenia treści
proste rozdzielcze strukturalne czasowe przestrzenne
z przedziałami z przedziałami okresów momentów
jednostkowymi wielojednostkowymi
(jednostopniowe) (wielostopniowe)
z równymi z nierównymi z równymi z nierównymi
przedziałami przedziałami przedziałami przedziałami
otwarte otwarte otwarte otwarte
zamknięte zamknięte zamknięte zamknięte
→ z punktu widzenia treści:
Szeregi strukturalne - oparte o cechę rzeczową (jakościową lub ilościową); umożliwiają one pogląd na wewnętrzną strukturę budowy zbiorowości
np. grupowanie pracowników wg wykształcenia, liczby dzieci, wieku
typ wykształcenia |
liczba pracowników |
wyższe średnie zas. zawodowe podstawowe |
|
szereg strukturalny
oparty o cechę rzeczową jakościową
liczba dzieci |
liczba pracowników |
0 1 2 3 |
|
szereg strukturalny
oparty o cechę rzeczową
mierzalną skokową
wiek |
liczba pracowników |
|
|
szereg strukturalny
oparty o cechę rzeczową
mierzalną ciągłą
Szeregi czasowe - oparte o cechę czasową; przedstawiają natężenie badanego zjawiska w czasie
szereg czasowy okresów - jeśli cecha ma charakter ciągły
szereg czasowy momentów - gdy zmienność cechy jest skokowa
lata |
liczba ludności |
1990 1991 . . 2000 |
|
Ludność Polski w latach 1990-2000.
Stan na 31.XII.2000.
szereg czasowy momentów
lata |
liczba ludności |
1990 1991 . . 2000 |
|
Ludność Polski w latach 1990-2000.
szereg czasowy okresów
Szeregi przestrzenne (geograficzne) - oparte są o cechę przestrzenną; przedstawiają natężenie badanego zjawiska w przestrzeni
np. liczba studentów w pięciu wybranych miastach Polski
miasto |
liczba studentów |
Warszawa Kraków Łódź Poznań Wrocław |
|
szereg przestrzenny
→ z punktu widzenia budowy (formy):
Szeregi proste (wyliczające, szczegółowe) - stosujemy je wówczas, gdy zbiorowość składa się z niedużej liczby jednostek, tzn. ≤ 30
np. lista obecności
Szeregi rozdzielcze - stosujemy je wówczas, gdy liczebność zbiorowości przekracza 30 jednostek; zbiorowość jest podzielona na określoną ilość klas wg zmienności interesującej nas cechy
szeregi rozdzielcze z przedziałami jednostkowymi - opierają się o cechę mierzalną skokową
szeregi rozdzielcze z przedziałami wielojednostkowymi - opierają się o cechę mierzalną ciągłą
Każdy z tych szeregów może mieć równe bądź nierówne przedziały klasowe; może być otwarty lub zamknięty.
szereg zamknięty - szereg, który ma określone wszystkie granice przedziałów klasowych
szereg otwarty - szereg, który ma otwartą jedną z granic przedziałów klasowych (zazwyczaj górną)
liczba dzieci |
liczba rodzin |
0 1 2 3 |
|
szereg rozdzielczy z przedziałami jednostkowymi
liczba punktów |
liczba studentów |
0-40 40-80 80-120 |
|
szereg rozdzielczy z przedziałami wielojednostkowymi, zamknięty,
o równych przedziałach klasowych
liczba punktów |
liczba studentów |
do 20 20-40 40-60 60 i więcej |
|
szereg rozdzielczy z przedziałami wielojednostkowymi, otwarty
lata |
liczba studentów |
1990-1992 1993-1996 1997-1998 1998-2000 |
|
szereg rozdzielczy z przedziałami wielojednostkowymi, zamknięty,
o nierównych przedziałach klasowych
ad. e.) Sporządzanie tablic statystycznych:
Tablica statystyczna jest formą prezentacji danych statystycznych. Praktyka i teoria statystyki wypracowały pewne zasady, których należy przestrzegać, aby tablice statystyczne spełniały swoją rolę.
Zasadniczo tablica statystyczna składa się z trzech części:
tytułu tablicy
tablicy właściwej
informacji na temat źródła powstania tablicy
Tytuł tablicy - powinien być zwięzły oraz zawierać określenie pod względem rzeczowym, czasowym i przestrzennym
powinien pokazywać cechy wg których dokonano grupowania
Tablica właściwa - składa się z kolumn i wierszy
wszystkie miejsca w tablicy właściwej muszą być wypełnione
jeśli nie podajemy w jakimkolwiek miejscu tablicy liczby, to należy ją zastąpić znakiem umownym
znaki umowne stosowane w tablicach statystycznych:
kreska ( -) - dane zjawisko nie wystąpiło
zero - dane zjawisko wprawdzie występuje, lecz jest tak nieliczne, że nie da się wyrazić w przyjętych w tablicy jednostkach miary
( 0 ) - zjawisko istniało w wielkości mniejszej od 0,5
( 0,0 ) - zjawisko istniało w wielkości mniejszej od 0,05
kropka ( . ) - brak wiarygodnych informacji o zjawisku
krzyżyk ( × ) - dane pole tablicy nie może być wypełnione ze względu na układ tablicy lub wypełnienie jest niecelowe
znak ( ♦ ) - występuje w Przeglądzie Międzynarodowym - oznacza, że dane dla Polski różnią się zakresem od danych w części krajowej Rocznika
znak ( Δ ) - nazwy zostały skrócone w stosunku do obowiązującej klasyfikacji
„w tym” - nie podaje się wszystkich składników sumy
wykrzyknik ( ! ) - umieszczany przy liczbach - liczba została zmieniona, poprawiona w porównaniu z liczbą poprzednio ogłoszoną
Źródło - podaje skąd zaczerpnięto dane, a także zawiera uwagi dotyczące informacji zawartych w tablicy.
Tablica statystyczna jest zbiorem szeregów - każda tablica może zawierać jeden lub więcej szeregów statystycznych - stąd wyróżniamy tablice:
proste - zawierają tylko jeden szereg statystyczny; grupowanie wg jednej interesującej nas cechy
kombinowane - zawierają więcej niż jeden szereg statystyczny; zbiorowość jest charakteryzowana wg co najmniej dwóch cech jednocześnie
W zależności od stopnia opracowania tablice dzielimy na:
robocze - służą do wstępnego opracowania materiału statystycznego - zawierają stosunkowo mało pozycji, nie nadają się do umieszczenia w publikacjach,
wynikowe - przeredagowane tablice robocze, zawierają wiele pozycji, są bardziej szczegółowe, zawierają zazwyczaj więcej niż jeden szereg statystyczny - są publikowane.
ad. f.) Sporządzanie wykresów statystycznych:
Wykres statystyczny -to inna forma prezentacji danych statystycznych; wykresem nazywam graficzny sposób przedstawienia zjawisk ujętych w szereg statystyczny.
Wykresy posiadają wiele zalet: są bardziej plastyczne i przejrzyste niż tablice statystyczne, stanowią cenny środek pomocniczy przy prezentacji danych, bo zawierają mniej szczegółów.
Wykresy składają się z trzech części:
tytuł wykresu,
wykres właściwy,
źródło na podstawie jakiego został sporządzony wykres.
Ważny jest wybór skali dla wykresu. Skale występujące w wykresach statystycznych mogą być:
równomierne - takie, w których jednakowym przedziałom graficznym odpowiadają jednakowe przedziały liczbowe,
nierównomierne - odznaczają się tym, że nierównym przedziałom graficznym odpowiadają jednakowe przedziały liczbowe lub odwrotnie; do skali tych zalicza się m.in. skalę logarytmiczną (zbudowaną wg postępu geometrycznego), semilogarytmiczną.
05-03-2001
Etap IV - analiza opracowanego materiału statystycznego.
Analiza statystyczna obejmuje:
analizę struktury
analizę współzależności
analizę dynamiki
a. ANALIZA STRUKTURY
Celem analizy struktury jest ustalenie podobieństw i różnic między jednostkami badanej zbiorowości ze względu na wyróżnioną cechę zmienną (analiza struktury dotyczy tylko jednej zmiennej - rzeczowej).
Podobieństwa między jednostkami ustala się przez wyznaczenie tzw. tendencji centralnej, czyli przeciętnego poziomu wartości cechy u wszystkich jednostek.
Badanie różnic między jednostkami przebiega wielokierunkowo i obejmuje:
analizę dyspersji (czyli rozproszenia),
analizę asymetrii (czyli skośności),
analizę koncentracji.
Sumaryczny opis badanej zbiorowości ze względu na przeciętny poziom i zróżnicowanie można uzyskać przy pomocy parametrów statystycznych. Parametry statystyczne dzielimy na klasyczne i pozycyjne.
Parametry statystyczne
PARAMETRY KLASYCZNE |
PARAMETRY POZYCYJNE |
MIARY PRZECIĘTNE |
|
Średnia arytmetyczna Średnia harmoniczna Średnia geometryczna Średnia potęgowa |
Dominanta Mediana Kwartyle
|
MIARY DYSPERSJI |
|
Odchylenie przeciętne Wariancja Odchylenie standardowe Typowy obszar zmienności Współczynnik zmienności |
Obszar zmienności Odchylenie ćwiartkowe Pozycyjny współczynnik zmienności |
MIARY ASYMETRII |
|
Współczynnik asymetrii Współczynnik α3 |
Pozycyjny współczynnik asymetrii |
MIARY KONCENTRACJI |
|
Współczynnik koncentracji Współczynnik α4 |
Stosunek koncentracji (krzywa Lorentza) |
Parametry klasyczne stosujemy gdy:
warianty badanej cechy charakteryzują się niewielkim stopniem wewnętrznego zróżnicowania,
szeregi statystyczne rozdzielcze są zamknięte i mają równe przedziały klasowe,
szeregi nie są skrajnie asymetryczne.
Parametry pozycyjne stosujemy gdy:
szeregi statystyczne rozdzielcze są otwarte lub posiadają nierówne przedziały klasowe,
chcemy sprawdzić wartość poznawczą parametru klasycznego,
chcemy uzyskać dodatkowe informacje o strukturze badanej zbiorowości.
MIARY PRZECIĘTNE |
Średnie klasyczne
Średnia arytmetyczna
w szeregu prostym: w szeregu rozdzielczym w szeregu rozdzielczym
jednostopniowym: wielostopniowym:
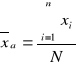
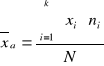
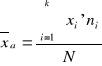
(śr. arytm. ważona) (śr. arytm. ważona)
gdzie: xi - warianty badanej cechy zmiennej
xi' - środki przedziałów klasowych
ni - wagi, tzn. liczebności częściowe
Właściwości średniej arytmetycznej:
parametr łatwy do obliczenia i interpretacji
liczba zawsze mianowana (określona co do swojej wartości)
jeżeli pomnożymy średnią arytmetyczną przez ogólną liczebność, to otrzymamy sumę wartości cech wszystkich jednostek zbiorowości:
![]()
suma odchyleń poszczególnych jednostek zbiorowości statystycznej od średniej arytmetycznej równa się zeru:
![]()
suma kwadratów odchyleń wartości poszczególnych jednostek zbiorowości statystycznej od średniej arytmetycznej równa się minimum:
![]()
obliczenie średniej arytmetycznej opiera się na wszystkich obserwacjach
średnią arytmetyczną można obliczyć dla szeregów o liczebnościach bezwzględnych i względnych
średnią arytmetyczną można obliczyć tylko dla zbiorowości jednorodnych
spełnia relację: xmin <
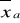
< xmax , co pozwala na ocenę logiczną parametruwadą jest to, że na wynik wpływ mają wartości skrajne
Średnia geometryczna
w szeregu prostym: w szeregu rozdzielczym:
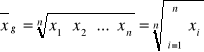
![]()
gdzie: n - liczba elementów
x1, x2, ..., xn - wartości szeregu w liczbach względnych
Π - znak iloczynu określonej liczby wyrazów
Właściwości średniej geometrycznej:
średnia geometryczna prosta jest n-tym pierwiastkiem z iloczynu wszystkich wartości szeregu
stosujemy ją wówczas, gdy wartości jednostek są wyrażone w liczbach względnych, a także gdy występują znaczne różnice między obserwacjami
średnia geometryczna jest mniej wrażliwa na wartości krańcowe niż średnia arytmetyczna
średnia geometryczna w swej wartości jest zawsze mniejsza od średniej arytmetycznej
średnia geometryczna różni się od innych średnich tym, że gdy obliczana jest dla szeregu, którego choć jedna wartość jest równa zero, to jej wartość też równa jest zero
Średnia harmoniczna
w szeregu prostym: w szeregu rozdzielczym:
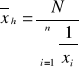
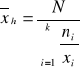
gdzie: xi - warianty badanej cechy
ni - wagi, tzn. liczebności cząstkowe
Właściwości średniej harmonicznej:
równa jest odwrotności średniej arytmetycznej z odwrotności poszczególnych jednostek zbiorowości
stosuje się ją gdy wartości jednostek podane są w formie odwrotności
używa się jej do obliczania m.in.: przeciętnego czasu potrzebnego do wyprodukowania jednostki wyrobu, siły nabywczej pieniądza, szybkości obrotów pieniężnych
Średnia potęgowa
ogólna formuła:
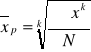
średnia kwadratowa jest pierwiastkiem kwadratowym ze średniej arytmetycznej kwadratów jednostek zbiorowości statystycznej:
w szeregu prostym: w szeregu rozdzielczym:
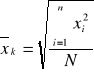
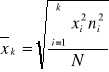
Podsumowanie:
wszystkie powyższe średnie należą do średnich klasycznych,
służą do sumarycznej charakterystyki wartości jednostek zbiorowości statystycznej,
wspólną ich cechą jest to, że ich wielkość zależy od wartości wszystkich jednostek zbiorowości,
średnie te należy traktować jako narzędzie analizy zwłaszcza przy porównywaniu 2 lub więcej zbiorowości,
wszystkie średnie sprowadzić można do średniej arytmetycznej za pomocą pewnych przekształceń,
każda z nich ma swoisty sens i musi być logicznie interpretowana,
wybór średniej zależy od charakteru zjawiska, które chcemy poznać.
Średnie pozycyjne
Miary przeciętne pozycyjne to wartości pewnych konkretnych jednostek zbiorowości wyodrębnione ze względu na ich położenie w danej zbiorowości.
Dominanta (modalna, wartość najczęstsza)
dominanta to wartość zmiennej, która największą ilość razy powtarza się w szeregu
w szeregu prostym:
np. 52, 53, 55, 55, 55, 63, 68 D = 55
w szeregu rozdzielczym jednostopniowym:
lata studiów |
liczba studentów |
1 |
610 |
2 |
103 |
3 |
360 |
4 |
315 |
5 |
290 |
D = 1
w szeregu rozdzielczym wielostopniowym:
![]()
(wzór interpolacyjny)
gdzie: xD - dolna granica przedziału, w którym znajduje się dominanta
CD - rozpiętość przedziału, w którym znajduje się dominanta
nD - liczebność przedziału dominanty
nD-1 - liczebność przedziału poprzedzającego przedział dominanty
nD+1 - liczebność przedziału następującego po przedziale dominanty
Własności dominanty:
stosujemy ją w statystykach płac, cen, w meteorologii, antropologii, zoologii
nadaje się do charakterystyki cech jakościowych
jest miarą najbardziej zrozumiałą wśród miar przeciętnych
należy do miar tendencji centralnej
na jej wartość liczbową nie mają wpływu wielkości skrajne
do jej wyznaczenia wystarczy znajomość 3 przedziałów klasowych o równej rozpiętości
można ją wyznaczyć w szeregu otwartym
dokładne wyznaczenie dominanty nie jest możliwe w szeregu rozdzielczym wielostopniowym
dominanta nie nadaje się do przekształceń algebraicznych
dominanty nie wyznacza się w szeregach bimodalnych lub wielomodalnych, gdyż obrazują one zbiorowości niejednorodne ze względu na cechę zmienną
Mediana (wartość środkowa)
jest to wartość jednostki statystycznej położonej w ten sposób, że liczba jednostek mających wartość nie mniejszą jest równa liczbie jednostek mających wartość nie większą od mediany
mediana dzieli szereg uporządkowany rosnąco lub malejąco na dwie części równe co do liczebności wyrazów
w szeregu prostym:
dla nieparzystej liczby wyrazów: ![]()
np. 48, 52, 58, 60, 61 Me = 58
dla parzystej liczby wyrazów: 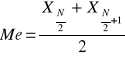
np. 48, 52, 58, 60, 61,64 Me = (58+60):2 = 59
w szeregu rozdzielczym:
dla nieparzystej liczby wyrazów: ![]()
dla parzystej liczby wyrazów: ![]()
gdzie: xd - dolna granica przedziału, w którym znajduje się mediana
N/2 - połowa liczebności, pozycja mediany
cum n-1 - skumulowana liczebność przedziałów poprzedzających przedział mediany
C0 - rozpiętość przedziału mediany
n0 - liczebność przedziału mediany
Właściwości mediany:
łatwa do obliczenia
niezależna od wartości krańcowych szeregu
można ją wyznaczyć nawet gdy nie wszystkie obserwacje są dokładnie znane
dokładność obliczenia mediany zależy od wielkości przedziałów klasowych - im mniejsze, tym obliczenia są dokładniejsze
można ustalić ją w szeregu otwartym
medianę można wyznaczyć tylko w szeregu uporządkowanym (jak wszystkie miary przeciętne pozycyjne)
mediana nie nadaje się do przekształceń algebraicznych
Kwartyle (wartości ćwiartkowe)
kwartyl 1
kwartyl 2 ( = mediana)
kwartyl 3
3
Wyszukiwarka
Podobne podstrony:
statystyka wyklady, Szkoła WSTiH
Statystyka opisowa wykład interpretacje
Statystyka opisowa, Wykład 9, 4
Wyklad statystyka opisowa 03 10 2010
wyklad 4 PODSTAWY STATYSTYKI OPISOWEJ
wyklad 4aa PODSTAWY STATYSTYKI OPISOWEJ
Statystyka opisowa, Wykład 10, 4
STATYSTYKA OPISOWA 4 WYKŁAD 29.03.2009 doc, STATYSTYKA OPISOWA 4 WYKŁAD 29
wykład 8 regresja, Statystyka opisowa
wyklad2 STATYSTYKA OPISOWA
statystyka opisowa, STATYSTYSTYKA OPISOWA pierwszy wykład 14. 02. 2009, STATYSTYSTYKA OPISOWA pierws
więcej podobnych podstron