Badanie zderzeń kul sprężystych

Ćwiczenie nr 6

Opis teoretyczny

Uproszczony schemat urządzenia pomiarowego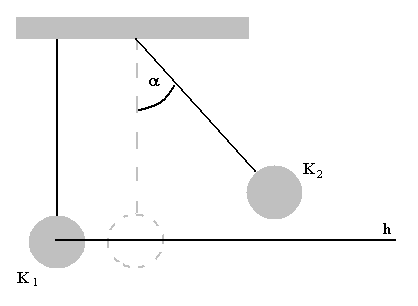
przedstawia rysunek. Składa się ono z dwu kul metalowych K₁ i K₂, zawieszonych na statywie za pomocą cienkich, izolowanych drutów. Kule tworzą wahadła, które możemy odchylać od pionu o zadany kąt α. Jeśli odchylimy wahadło K₂ i przytrzymamy w tym położeniu przy pomocy elektromagnesu, a następnie zwolnimy, to uderzy ono w nieruchome wahadło K₁ i przekaże mu swój cały pęd (cały jeśli kule mają jednakowe masy, lub część pędu, jeśli masy kul są różne). Umieszczenie małego kawałka plasteliny pozwala badać zderzenia niesprężyste. Prawa zachowania pędu i energii kinetycznej przy zderzeniach kul sprężystych mają postać:

m₁v₁+m₂v₂=m₁u₁+m₂u­₂ (1)

i (2)

gdzie m₁ i m₂ oznaczają odpowiednio masy kul K₁ i K₂, v₁ i v₂ ich prędkości przed zderzeniem, u₁ i u₂ich prędkości po zderzeniu.

Prawo zachowania pędu przy zderzeniach kul niesprężystych ma postać:

m₁v₁+ m₂v₂=( m₁+m₂)u (3)

gdzie u jest prędkością wspólną obu kul po zderzeniu.

Dla pełnego bilansu energii musimy jeszcze uwzględnić energię potencjalną U=mgh kuli wychylonej z położenia równowagi:

Związek miedzy h i α ma postać:

h=L₀(1-cosα) (5)

gdzie L₀ oznacza długość wahadła. Na podstawie wzorów (4) i (5) można obliczyć maksymalną prędkość, jaką ma kula K₂ w momencie zderzenia z kulą K₁

a stąd maksymalną wartość pędu i energii kuli K₂.

Teoria zderzeń kul sprężystych została opracowana przez H. Hertza w 1881 roku. Z teorii tej wynika, że czas zderzeń kul jest proporcjonalny do promienia kuli R i odwrotnie proporcjonalny do ich względnej prędkości w potędze 1.5, czyli:

Przebieg doświadczenia i obliczenia

1. Aby sporządzić wykres zależności ∆t od prędkości v₂ w układzie podwójnie logarytmicznym, liczymy najpierw wartości średnie czasów ∆t dla 10-ciu pomiarów, a następnie prędkość kuli K₂ przy zderzeniu z kulą K_1­, czyli:

,gdzie L₀=L+d/2, gdzie d-średnica kulki

Dla zderzeń dwóch kul dużych:

• dla α=2°, ∆t_1śr=220 μs

• dla α=7°, ∆t_2śr=176 μs

• dla α=15°, ∆t_3śr=98 μs

Dla zderzeń dwóch kul małych:

• dla α=2°, ∆t_1śr=191,1 μs

• dla α=7°, ∆t_2śr=144,(3) μs

• dla α=15°, ∆t_3śr=121,1 μs

a prędkość v₂ , dla kul dużych wynosi dla α odpowiednio:

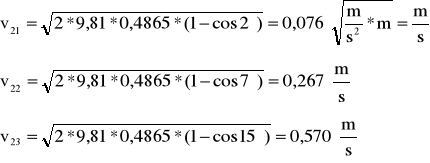
a prędkość v₂ , dla kul małych wynosi dla α odpowiednio:

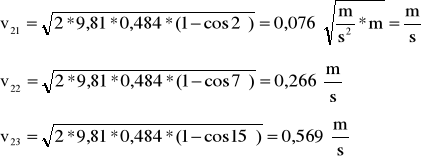
Biorąc pod uwagę rozkład Gaussa odrzuciłem pomiary przypadkowe.

Wykresy zależności ∆t od prędkości v₂ znajdują się odpowiednio na rysunku 1, dla kul dużych i na rysunku 2, dla kul małych. Wykresy te wykonałem w Excelu. Tam też obliczyłem nachylenie prostej, które wynosi odpowiednio:

• dla kul dużych = -0,38 ≈ -2/5

• dla kul małych = -0,22 ≈ -1/5

Jednakże wydaje mi się, iż dla kul dużych wykonaliśmy to doświadczenie mało poprawnie, gdyż urządzenie do mierzenia czasu mierzy czas najdokładniej wtedy, gdy kulki są idealnie nieruchome. Na pewno doświadczenie to wykonaliśmy znacznie lepiej dla kul małych, gdyż dopiero wtedy staraliśmy się idealnie zatrzymać kulki po zderzeniu.

Z tych rozważań wynika, iż wykładnik potęgi we wzorze Hertza jest równy -1/5

Następnie sprawdzamy prawo zachowania pędu w zderzeniach sprężystych. W tym celu obliczamy maksymalną prędkość kulki K₂ w chwili zderzenia z kulką nieruchomą K₁dla pięciu kątów wychylenia α, a następnie maksymalną wartość pędu.

Maksymalna prędkość kulki K₂ wynosi:

Dla kulek o tych samych masach, w zderzeniach sprężystych prędkość maksymalna wynosi:

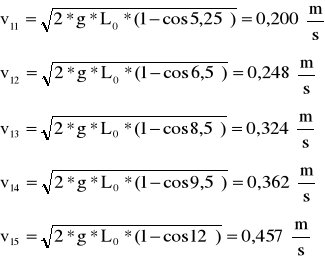
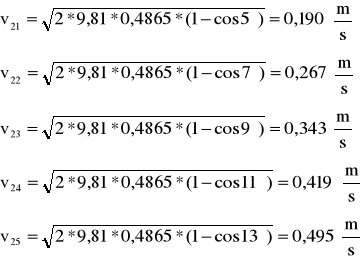
Dla kulek o masie m₂=180,5g=0,1805kg

A maksymalna wartość pędu wynosi

przed zderzeniem: po zderzeniu:

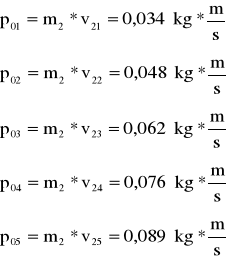
Dla kulek o masie m₁=111,46g=0,11146kg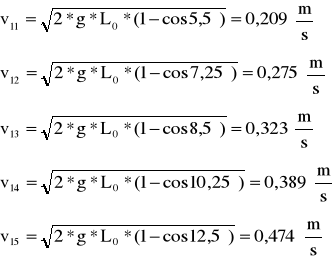

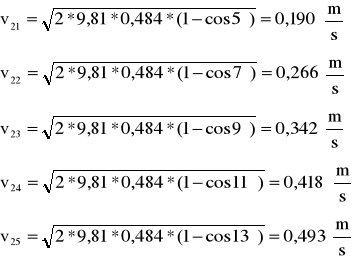
A maksymalna wartość pędu wynosi

przed zderzeniem: po zderzeniu:

Dla kulki m₁ uderzającą w m₂: L_0'=0,4865

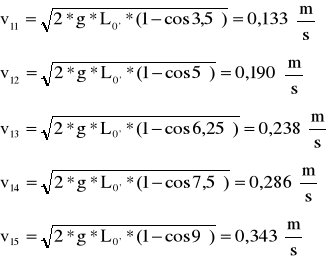
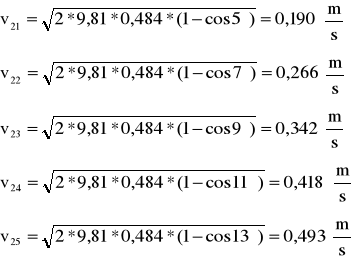
A maksymalna wartość pędu dla m­₁→m₂ wynosi_­

przed zderzeniem: po zderzeniu:

Dla kulki m₂ uderzającą w m₁: L_0'=0,484

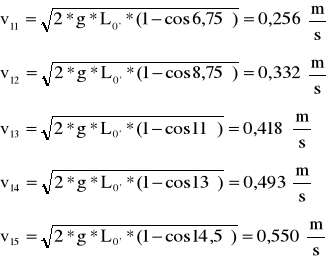
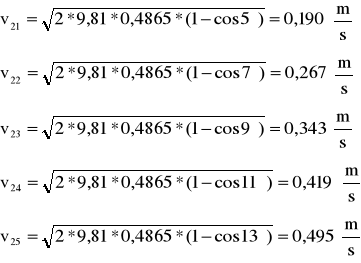
A maksymalna wartość pędu dla m­₂→m₁ wynosi_­

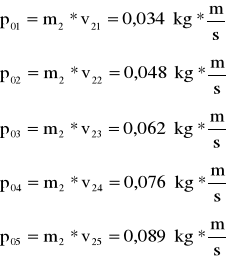
przed zderzeniem: po zderzeniu:

Sprawdzamy prawo zachowania pędu w zderzeniach niesprężystych. W tym celu korzystamy z wzoru (3), czyli

m₁v₁+ m₂v₂=( m₁+m₂)u

Najpierw obliczamy v₂, u, p1, p2, dla zderzeń niesprężystych dwóch kulek o masach m₂=0,1805, gdzie:

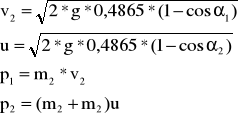
α1	v2	α2	u	m	p1	p2
5	0,191	2,75	0,105	0,1805	0,034	0,038
7	0,267	3,75	0,143	0,1805	0,048	0,052
9	0,343	4,5	0,172	0,1805	0,062	0,062
11	0,419	5,5	0,210	0,1805	0,076	0,076
13	0,495	7	0,267	0,1805	0,089	0,096

Obliczamy v₂, u, p1, p2, dla zderzeń niesprężystych dwóch kulek o masach m₁=0,11146, gdzie:

α1	v2	α2	u	m	p1	p2
5	0,190	2,75	0,105	0,11146	0,021	0,023
7	0,266	3,75	0,143	0,11146	0,030	0,032
9	0,342	4,5	0,171	0,11146	0,038	0,038
11	0,418	5,75	0,219	0,11146	0,047	0,049
13	0,493	7,25	0,276	0,11146	0,055	0,061

Obliczamy v₂, u, p1, p2, dla zderzeń niesprężystych dwóch kulek m₁=0,11146 w m₂=0,1805 gdzie:

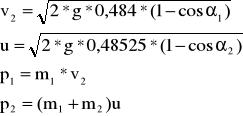
α1	v2	α2	u	m1	p1	m2	p2
5	0,190	2,25	0,086	0,11146	0,021	0,1805	0,025
7	0,266	3	0,114	0,11146	0,030	0,1805	0,033
9	0,342	3,25	0,124	0,11146	0,038	0,1805	0,036
11	0,418	4,25	0,162	0,11146	0,047	0,1805	0,047
13	0,493	5,25	0,200	0,11146	0,055	0,1805	0,058

Obliczamy v₂, u, p1, p2, dla zderzeń niesprężystych dwóch kulek m₂=0,1805 w m₁=0,11146 gdzie:

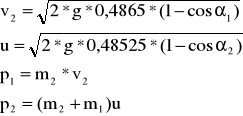
α1	v2	α2	u	m1	p1	m2	p2
5	0,191	3,25	0,124	0,1805	0,034	0,11146	0,036
7	0,267	4,75	0,181	0,1805	0,048	0,11146	0,053
9	0,343	6	0,228	0,1805	0,062	0,11146	0,067
11	0,419	7	0,266	0,1805	0,076	0,11146	0,078
13	0,495	8,25	0,314	0,1805	0,089	0,11146	0,092

Ocena błędów i wnioski

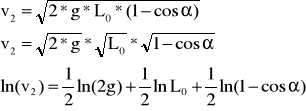
Wyznaczamy błąd Δv₂ metodą pochodnej logarytmicznej. W tym celu logarytmujemy obie strony równania (6), czyli

A następnie różniczkujemy obustronnie to równanie i zastępujemy różniczki odpowiednimi wartościami błędów:

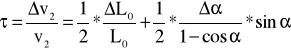
Np.	α[°]	τ
1	5	0,0510
2	7	0,0367
3	9	0,0288
4	11	0,0237
5	13	0,0202

Szacunkowo błędy te nie są znaczne. Spowodowane są przede wszystkim niedokładnością ludzkiego oka, a także małą dokładnością skali dla kątów.

Ponadto przy sprawdzaniu prawa zachowania pędu można wywnioskować, iż nie jest to zderzenie idealnie sprężyste. Dzieje się tak, ponieważ kulki nie trafiają w siebie centralnie, oraz część energii jest zamieniana na energię cieplną. Te małe rozbieżności doskonale ukazują rysunki 3 - 10. Doskonale na nich widać, że pęd przed zderzeniem jest prawie równy pędowi po zderzeniu.

Przy sprawdzaniu prawa Hartza, można dojść do słuszności wzoru (7), czyli:

Gdyż nachylenie prostej zależności t od v₂ jest w przybliżeniu równe -1/5.

1

1

Marcin Grześczyk

I rok „bis” - Fizyka

29.10.1999

dr T. Biernat

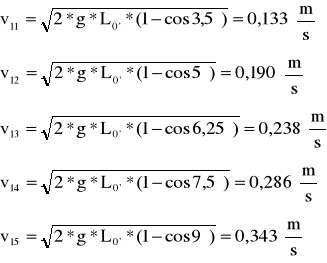
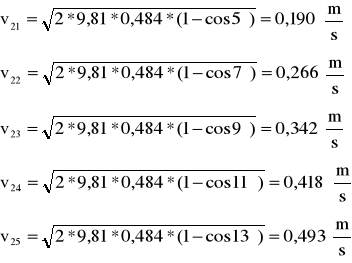
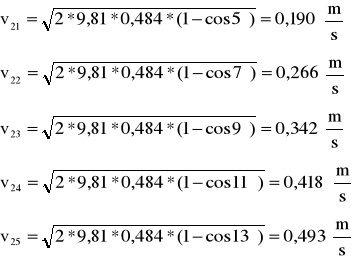
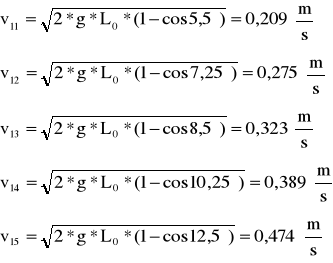
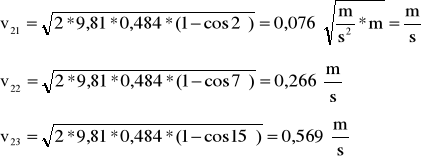
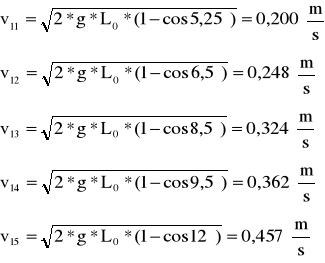
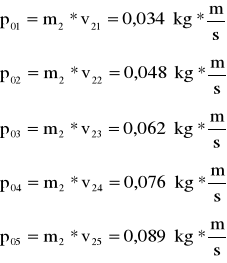
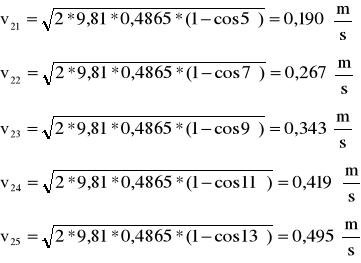
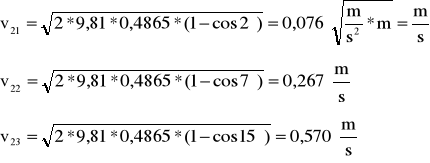
(7)

(6)

(4)

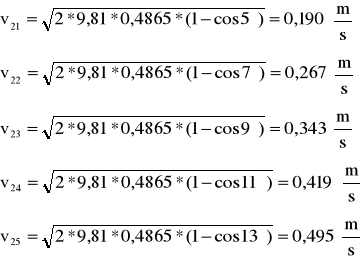
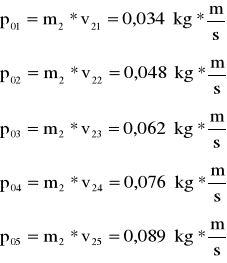
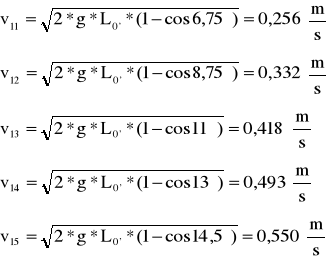
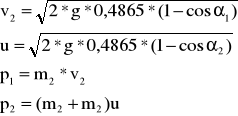
v₂ - prędkość kuli K₂ przy zderzeniu z kulą K₁

u - prędkość kul K₂ i K­₁ połączonych

p₁ - pęd kuli K₂

p₂ - pęd kul K₂ i K₁połączonych

v₂ - prędkość kuli K₂ przy zderzeniu z kulą K₁

u - prędkość kul K₂ i K­₁ połączonych

p₁ - pęd kuli K₂

p₂ - pęd kul K₂ i K₁połączonych

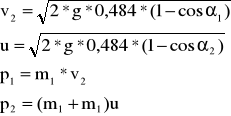
v₂ - prędkość kuli K₂ przy zderzeniu z kulą K₁

u - prędkość kul K₂ i K­₁ połączonych

p₁ - pęd kuli K₂

p₂ - pęd kul K₂ i K₁połączonych

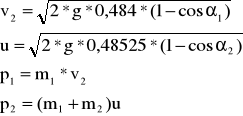
v₂ - prędkość kuli K₂ przy zderzeniu z kulą K₁

u - prędkość kul K₂ i K­₁ połączonych

p₁ - pęd kuli K₂

p₂ - pęd kul K₂ i K₁połączonych

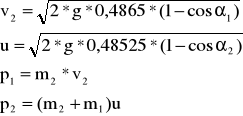
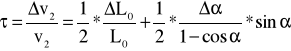
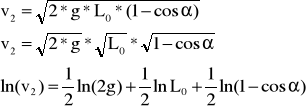
L₀=0,469m

ΔL₀=0,001m

Δα=0,25°=0,00436

---