ZADANIA ELEMENTARNE - Język matematyki. Elementy logiki. Zbiory
Podaj dwa przykłady alternatywy: prawdziwą i nieprawdziwą.
Podaj dwa przykłady koniunkcji: prawdziwą i nieprawdziwą.
Podaj dwa przykłady implikacji: prawdziwą i nieprawdziwą.
Podaj dwa przykłady równoważności: prawdziwą i nieprawdziwą.
Oceń wartości logiczne zdań składowych i zdań złożonych:

,
,
,

, jeśli p i q mają następującą treść:
a) p: Przeciwprostokątna w trójkącie prostokątnym jest krótsza o każdej z przyprostokątnych.
q: Przeciwprostokątna w trójkącie prostokątnym jest dłuższa od sumy długości przyprostokątnych.
b) p: Milicz to miasteczko nad Wisłą, q: Milicz to miasteczko w kraju nad Wisłą.
W podpunktach a i b sformułuj też brzmienia całych zdań złożonych - w sensownej uproszczonej formie.
b) p: ![]()
, q:![]()
, c) p:![]()
, q:![]()
, d) p:![]()
, q:![]()
,
Niech n będzie liczbą całkowitą. Podaj pełne brzmienie następujących zdań i oceń ich wartości logiczne:
a) ![]()
, b)![]()
, c)![]()
, d)![]()
Dane jest zdanie: Jeśli latawiec leci, to jest wiatr. Sformułuj to zdanie w postaci: a) implikacji przeciwstawnej, b) implikacji odwrotnej, c) implikacji przeciwnej, d) alternatywy. Sformułuj w postaci koniunkcji zaprzeczenie danego zdania. Oceń wszystkie powyższe zdania.
Dane jest zdanie:

. Sformułuj pełne brzmienie tego zdania. Sformułuj to zdanie w postaci a) implikacji przeciwstawnej, b) implikacji odwrotnej, c) implikacji przeciwnej. Sformułuj w postaci koniunkcji zaprzeczenie danego zdania. Oceń wszystkie powyższe zdania.Zastosuj prawo zaprzeczenia alternatywy do zaprzeczenia następujących zdań:
a) Świeci słońce lub pada deszcz, b) Jestem w szkole lub w domu, c) Kocham Dodę lub Mandarynę,
d) Nie jestem głodny lub spokojny, e) Nie siedzę nad matmą lub wszystko rozumiem, f) Jasiu jest niemądry lub leniwy. g) To zdanie jest bezsensowne lub długie, h) Temperatura jest dodatnia lub nie wieje wiatr, i) ![]()
, j)![]()
, k)![]()
. Oceń zdania j, k.
Zastosuj prawo zaprzeczenia koniunkcji do zaprzeczenia następujących zdań:
a) Jasiu jest piękny i młody, b) Jasiu jest zdolny i pracowity, c) Kocham Dodę i Mandarynę, d) To zdanie jest niemądre i długie, e) Dzień jest wietrzny i bezchmurny, f) Temperatura jest nieujemna i mniejsza od 10 oC, g) Jestem głodny i zły, h)![]()
, i) ![]()
, j) ![]()
. Oceń zdania i, j.
Dane są zbiory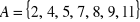
,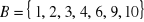
. Narysuj te dwa zbiory na diagramie i wyznacz:
a) ![]()
, b) ![]()
, c) ![]()
, d) ![]()
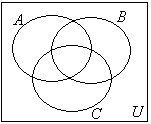
Na diagramie Venna (rysunek obok) zaznacz następujące zbiory:
a)![]()
, b)![]()
, c)![]()
, d)![]()
, e)![]()
, f)![]()
, g)![]()
, h)![]()
.
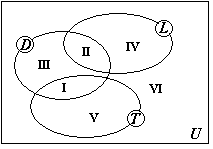
Na diagramie obok przedstawiono zbiory:
T - uczniowie (chłopcy i dziewczęta) technikum, L - uczniowie (chłopcy i dziewczęta) liceum, D - dziewczęta. Przestrzeń U tworzą wszyscy uczniowie Zespołu Szkół w skład którego wchodzią: LO, T, ZSZ. Opisz obszary zaznaczone liczbami rzymskimi.
Na osi liczbowej (rysunek poniżej) są przedstawione przedziały A i B.
Zapisz te przedziały oraz wyznacz ![]()
, ![]()
, ![]()
, ![]()
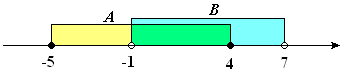
Narysuj na osi liczbowej przedziały A i B oraz wyznacz następujące zbiory:
a) ![]()
,![]()
, b)![]()
,![]()
, c)![]()
,![]()
, d)![]()
,![]()
, e) ![]()
,![]()
.
Niech
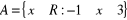
,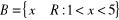
. Przedstaw te zbiory na osi liczbowej oraz wyznacz ich sumę i iloczyn.Niech
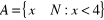
,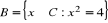
. Wyznacz elementy obu zbiorów oraz
,
,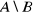
,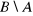
Przykład: ![]()
.
Wyznacz podobnie jak w przykładzie:
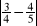
,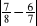
,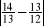
,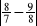
.
Przykłady: aby wyznaczyć wartość bezwzględną liczby ![]()
badamy najpierw jej znak: ![]()
. Zatem ![]()
.
Podobnie ![]()
, natomiast ![]()
(dlaczego?)
Wyznacz podobnie jak w przykładzie:
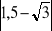
,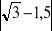
,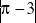
,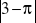
.
Przykłady: Równanie ![]()
czytamy: „odległość x od 0 wynosi 10”. Zatem x znajduje się na osi liczbowej 10 jednostek na lewo od 0 lub 10 jednostek na prawo od 0, stąd ![]()
lub ![]()
.
Podobnie ![]()
![]()
![]()
![]()
![]()
, zatem ![]()
.
Rozwiąż podobnie jak w przykładzie: a)
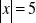
, b)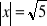
, c)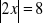
, d)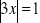
, e)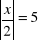
, f)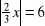
, g)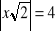
.
Przykłady: Równanie ![]()
czytamy: „odległość x od 8 jest równa 10”. Zatem x znajduje się na osi liczbowej 10 jednostek na lewo od 8 lub 10 jednostek na prawo od 8, stąd równanie ma dwa rozwiązania: ![]()
lub ![]()
.
Podobnie ![]()
: „odległość ![]()
od 7 wynosi 3”, zatem ![]()
lub ![]()
, a stąd: ![]()
.
Można też tak: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
(wyjaśnij przekształcenia).
Podobnie ![]()
![]()
![]()
: „odległość x od -8 wynosi 10”, zatem ![]()
.
Rozwiąż, jak w przykładzie: a)
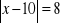
, b)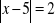
, c)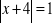
, d)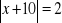
, e)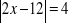
, f)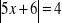
, g)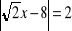
.
Przykłady: Nierówność: ![]()
czytamy: „odległość x od 0 jest mniejsza od 5”, zatem na osi liczbowej rozwiązania tej nierówności znajdują się na prawo od -5 i jednocześnie na lewo od 5: ![]()
, zatem![]()
.
Podobnie nierówność ![]()
czytamy: „odległość x od 0 jest mniejsza lub równa (czyli niewiększa!) od 15, a to znaczy, że ![]()
.
Rozwiąż podobnie jak w przykładzie: a)
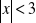
, b)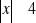
, c)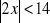
, d)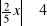
, e)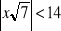
.
Przykłady: Nierówność ![]()
czytamy: „odległość x od 10 jest mniejsza od 2”, a to znaczy, że na osi liczbowej rozwiązania tej nierówności znajdują się pomiędzy liczbami 10-2=8, a 10+2=12, czyli ![]()
.
Podobnie ![]()
czytamy: „odległość x od -5 jest mniejsza lub równa (niewiększa) od 1, zatem na osi liczbowej x znajduje się na prawo od ![]()
(włącznie) i jednocześnie na lewo od ![]()
(też włącznie), zatem ![]()
Rozwiąż podobnie jak w przykładzie: a)
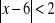
, b)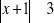
, c)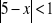
, d)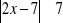
, e)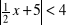
.
Przykłady: Nierówność ![]()
czytamy: „odległość x od 0 jest większa od 6”, zatem na osi liczbowej x jest na lewo od liczby -6 lub też na prawo od liczby 6: ![]()
, zatem ![]()
.
Podobnie ![]()
czytamy: „odległość x od 10 jest większa lub równa (niemniejsza) od 1”, czyli na osi liczbowej x jest na lewo od ![]()
(włącznie) lub też na prawo od ![]()
, więc ![]()
, zatem: ![]()
.
Rozwiąż podobnie jak w przykładzie: a)
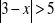
, b)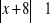
, c)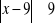
, d)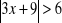
, e)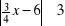
.Niech
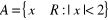
,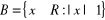
. Zapisz A i B w postaci przedziałów i wyznacz
,
,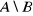
,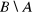
.Niech
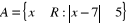
,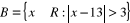
.
Zapisz A i B w postaci przedziałów i wyznacz
,
,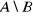
,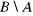
.
1
Wyszukiwarka
Podobne podstrony:
zadania - algebra 1, nauka, matematyka, LICEUM, 1 KLASA, I RÓWNANIA I NIERÓWNOŚCI
zadania - symetria, nauka, matematyka, LICEUM, 2 KLASA, II FIGURY I PRZEKSZTAŁCENIA
zadania - pitagoras, nauka, matematyka, LICEUM, 1 KLASA, II FIGURY GEOMETRYCZNE
zadania - symetria 1, nauka, matematyka, LICEUM, 2 KLASA, II FIGURY I PRZEKSZTAŁCENIA
zadania - koło 1, nauka, matematyka, LICEUM, 2 KLASA, II FIGURY I PRZEKSZTAŁCENIA
zadania - koło, nauka, matematyka, LICEUM, 2 KLASA, II FIGURY I PRZEKSZTAŁCENIA
zadania - pola figur 2, nauka, matematyka, LICEUM, 1 KLASA, II FIGURY GEOMETRYCZNE
zadania - pola figur, nauka, matematyka, LICEUM, 1 KLASA, II FIGURY GEOMETRYCZNE
kartkowka 6, nauka, matematyka, LICEUM, 1 KLASA, II FIGURY GEOMETRYCZNE
kartkowka 5, nauka, matematyka, LICEUM, 1 KLASA, II FIGURY GEOMETRYCZNE
logika zadania 1-2, logika
Kombinatoryka - Zadania, Nauka, Matematyka, Kombinatoryka. Prawdopodobieństwo
Zadania dla maturzystów na dzień 28 marca 2010, matematyka, LICEUM, arkusze maturalne, Nowy folder (
Zadania logika
zadania2, Matematyka, Liceum
Zadania geograficzne z elementami matematyki 2, Nauka, Pomoce dydaktyczne, Zadania
zadania logika1
Test na wejsciu z fizyki do liceum, Konspekty szkolne i zadania z fizyki oraz matematyki (haslo- kwa
Planimetria - Zadania, Nauka, Matematyka
więcej podobnych podstron