W trójkącie prostokątnym środkowa poprowadzona z wierzchołka kąta prostego dzieli ten kąt w stosunku 1:2. Wyznacz kąty ostre tego trójkąta.
Wierzchołki trójkąt ABC należą do okręgu o środku O. Oblicz miary kątów tego trójkąta, wiedząc, że |<ACB |=100°, |<ACO|=30°.
Przez wierzchołek A trójkąta ABC poprowadzono prostą l, dzielącą środkową CD w stosunku 2:3 licząc od wierzchołka C. W jakim stosunku prosta l dzieli bok BC tego trójkąta?
Dany jest trójkąt prostokątny ABC o przyprostokątnych CA i CB. W trójkącie tym poprowadzono wysokość CH i środkową AM. Wiedząc, że |CA|=
i |CB|=
, oblicz pole trójkąta MBH.Dany jest trójkąt prostokątny o przyprostokątnych a=5cm i b=12cm. Oblicz promień okręgu wpisanego w ten trójkąt oraz okręgu opisanego na tym trójkącie.
Dany jest równoległobok o bokach a i b. Oblicz sinus kąta ostrego tego równoległoboku, wiedząc, że prosta prostopadła do dwóch jego boków równoległych dzieli go na dwa trapezy, w które można wpisać okręgi.
W równoległoboku o kącie ostrym równym 60° krótsza przekątna ma długość
cm. Oblicz długości boków równoległoboku, wiedząc, że jeden z nich jest o 2cm dłuższy od drugiego.Niech H będzie punktem przecięcia wysokości trójkąta ostrokątnego ABC. Znajdź kąty tego trójkąta, wiedząc, że |<BAH|=α i |<ABH|=β.
W trójkącie ABC dane są |AB|=8m |AC|=6 i |BC|=
. Oblicz miarę kąta BAC.W trójkącie ABC dane są |CB|=
i |<BAC|=60°. Oblicz długości pozostałych boków trójkąta, wiedząc, że jeden z nich jest dwa razy dłuższy od drugiego.W trójkącie prostokątnym ABC (|<BCA|=90°) z wierzchołka C poprowadzono wysokość CD. Punkty M i N są środkami odcinków AD i DB. Wiedząc, że pole trójkąta ABC jest równe S, oblicz pole trójkąta MNC.
W równoległoboku przekątne o długościach 12 i 10 tworzą kat o mierze 60°. Oblicz pole i obwód tego równoległoboku.
W trapezie długości podstaw są równe 15cm i 2cm, a długości ramion - 5cm i 12 cm. Oblicz pole trapezu.
Na trójkącie ABC, w którym |BC|=a, |<ABC|=α i |<BCA|=β, opisano okrąg. Dwusieczna kąta przy wierzchołku A przecina okrąg w punkcie K. Oblicz długość odcinka AK.
W okrąg wpisano dwa trójkąty o wspólnej podstawie. Stosunek długości ramion tych trójkątów wynosi 1:3. Oblicz stosunek długości wysokości opuszczonych na wspólny bok.
W trójkącie prostokątnym poprowadzono dwusieczną kąta prostego. Oblicz kąty ostre trójkąta, wiedząc, że środek okręgu wpisanego dzieli odcinek dwusiecznej w stosunku
, licząc od wierzchołka kąta prostego.Na boku AB trójkąta ABC obrano M i N tak, że |AM|:|MN|:|NB|=1:2:3. Przez punkty Mi N poprowadzono proste równoległe do boku AC, przecinające bok BC odpowiednio w punktach M' i N'. Oblicz pole czworokąta MNN'M', jeśli pole trójkąta ABC wynosi S.
W trójkąt wpisano okrąg o promieniu 3cm. Oblicz pole trójkąta, jeżeli punkt styczności dzieli jeden z boków na odcinki o długościach 3cm i 4cm.
W trapezie równoramiennym podstawy mają długości 6 i 15, a przekątna zawiera się w dwusiecznej kąta ostrego trapezu. Oblicz pole i obwód trapezu.
W trójkącie prostokątnym ABC zachodzą własności:
oraz
.
Oblicz miary kątów.
W trójkącie ABC poprowadzono środkową z wierzchołka C, która przecina bok AB w punkcie D. Przez środek środkowej CD poprowadzono prostą równoległą do boku AC, która przecina boki AB i CB odpowiednio w punktach E i F. Wiedząc, że |CF|=5, znajdź długość odcinka BF.
Dany jest trójkąt równoramienny ABC, gdzie długość ramion AC i BC wynosi
. Wysokość opuszczona na podstawę trójkąta jest równa odcinkowi łączącemu środek podstawy ze środkiem ramienia.Oblicz różnicę między długością promienia opisanego na trójkącie ABC i długością promienia wpisanego w dany trójkąt ABC.
Do okręgu wpisanego w trójkąt ABC poprowadzono styczną równoległą do podstawy, przecinającą ramiona trójkąta w punktach M i N. Znajdź długość odcinka MN.
W trapezie równoramiennym ABCD, gdzie AB || CD, kąty ostre mają miarę 30°. Stosunek dłuższej podstawy do krótszej wynosi 5:3. Przekątne trapezu tworzą z jego ramionami kąt 135°.
Oblicz pole i obwód trapezu, jeżeli długość ramienia BC wynosi 2.
Wyznacz stosunek promienia okręgu opisanego na trójkącie ABD do promienia okręgu opisanego na trójkącie BCD.
W trójkącie ABC wysokość |CD|=4, bok |BC|=8, |<BAC|=60°. Punkty M, N, P są środkami boków trójkąta ABC. Oblicz długości boków i pole trójkąta MNP.
Na bokach AB, BC i CA trójkąta ABC dane są odpowiednio punkty M, N i P takie, że
. Wyznacz k, jeśli pole trójkąta MNP jest równe
pola trójkąta ABC.Dany jest trójkąt ABC, w którym miara kąta BCA wynosi 90°, a kąt CAB jest dwa razy mniejszy od kąta ABC. Obwód okręgu wpisanego w ten trójkąt wynosi
. Prosta przechodząca przez wierzchołek C tworzy z krótszą przyprostokątną kąt o mierze 30° i przecina przeciw prostokątną AB i punkcie D.Oblicz pole koła opisanego na trójkącie oraz wyznacz stosunek długości odcina DB do długości odcinka DA.
Oblicz odległość punktu D od środka okręgu wpisanego w trójkąt ABC.
W trapezie równoramiennym dane są długości podstaw a i b ( a > b ) i kąt ostry α=60°. Środki sąsiednich boków trapezu połączono odcinkami. Oblicz pole czworokąta, którego bokami są te odcinki oraz wyznacz stosunek pola trapezu do pola powstałego czworokąta.
W trapezie równoramiennym ABCD ( AB || CD ), w którym kąt ostry jest równy 45°, przekątna AC długości 2 tworzy z podstawą AB kąt 30°.
Oblicz pole i obwód trapezu.
Wykaż, że długości promieni okręgów opisanych na trójkątach ABC i ACD są równe długości ramienia trapezu.
W równoległoboku ABCD dale są długości boków |AB|=5, |AD|=3 oraz miara kąta ostrego DAB równa 60°. Punkty E i F są odpowiedni środkami boków BC i DC.
Oblicz długości przekątnych równoległoboku oraz pole czworokąta BEFD.
Wyznacz sumę kwadratów sinusów katów wewnętrznych trójkąta ABD.
W trójkącie równobocznym ABC o polu
na boku BC obrano punkt M tak, że |BM|=
|MC|.Oblicz sinus kąta MAB oraz długość promienia okręgu wpisanego w trójkąt MAB.
Jakie długości mają odcinki, na które symetralna AM dzieli bok AB?
W trapezie równoramiennym ABCD (gdzie AB || CD ) kąty ostre mają miarę 30°. Stosunek długości dłuższej podstawy do krótszej wynosi 5:3. Przekątne trapezu tworzą z jego ramionami kąt 135°.
Oblicz pole i obwód trapezu, jeżeli długość ramienia |BC|=2.
Wyznacz stosunek promienia okręgu opisanego na trójkącie ABD do promienia okręgu opisanego na trójkącie BCD.
W trójkącie ABC dane są długości boków |AB|=
, |AC|=10 oraz
.Oblicz odległość wierzchołka A od prostej BC.
Oblicz sumę długości promieni okręgu opisanego na trójkącie ABC i okręgu wpisanego w trójkąt ABC.
Udowodnij, że pole trójkąta wyraża się wzorem:
.Promień okręgu opisanego na trójkącie ABC wynosi 3. Wiedząc, że
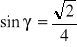
oraz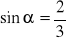
, oblicz długości boków BC i BA.W trójkącie równoramiennym ABC kąt między ramionami wynosi α. Oblicz stosunek długości promienia okręgu wpisanego w trójkąt ABC do długości promienia okręgu opisanego na trójkącie ABC.
Długości podstaw trapezu ABCD wynoszą a i c. Znajdź miary kątów i długości przekątnych tego trapezu.
Podstawa
Różnica pól dwóch kwadratów jest równa 36. Oblicz wartość bezwzględną różnicy pól kół opisanych na tych kwadratach.
Różnica pól dwóch trójkątów równobocznych jest równa
. Oblicz wartość bezwzględną różnicy pól kół wpisanych w te trójkąty.Pole prostokąta, w którym jeden z boków jest o 4 cm dłuższy od drugiego, jest równe 96 cm2. Oblicz pole koła opisanego na tym prostokącie. Wynik podaj w mm2 z zaokrągleniem do drugiego miejsca po przecinku.
Bok rombu ma długość 20 cm, a jego kąt ostry miarę 80°, Oblicz długość dłuższej przekątnej tego rombu. Wyniki podaj w mm z zaokrągleniem do pierwszego miejsca po przecinku.
W trójkącie ABC wysokość CD dzieli bok AB na odcinki Ad i DB takie, że
. Miara kąta ABC jest równa 30°. Uzasadnij, ze trójkąt ABC jest trójkątem prostokątnym.Przekątne równoległoboku ABCD mają długości 18 cm i 22 cm. Środki boków tego równoległoboku są wierzchołkami czworokąta KLMN. Oblicz obwód czworokąta KLMN.
W trapezie równoramiennym ABCD, w którym AB || CD oraz |AB|=20, |CD|=12, |AD|=|BC|=8, przedłużono boki AD i BC do przecięcia w punkcie E. Oblicz:
długość odcinka AE,
odległość punktu E od prostej AB.
W trójkącie równoramiennym, w którym ramiona mają długość 10 cm i sinus kąta przy podstawie jest równy 0,(6), połączono środki ramion, dzieląc w ten sposób trójkąt wyjściowy na trójkąt i czworokąt. Oblicz obwód czworokąta. Wynik podaj w cm z zaokrągleniem do drugiego miejsca po przecinku.
W trójkącie ABC, w którym |AB|=10 cm, |BC|=8 cm, cos|<ABC|=0,(3), na boku BC wybrano punkt D taki, że |BD|=2 cm. Prosta równoległa do prostej AB przechodząca przez punkt D przecina bok AC w punkcie E. Oblicz pole czworokąta ABDE. Wynik podaj w mm2 z zaokrągleniem do drugiego miejsca po przecinku.
W trójkącie równoramiennym ABC : |AB|=24 i |AC|=|BC|= 13 . W trójkąt ten wpisano kwadrat DEFG tak, że bok DE zawarty jest w podstawie trójkąta, a wierzchołki F i G należą do ramion trójkąta. Oblicz długość boku tego kwadratu.
W trójkącie równoramiennym ABC : |AB|=16 i |AC|=|BC|=10. W trójkąt ten wpisano prostokąt DEFG tak, że bok DE jest zawarty w podstawie trójkąta, a wierzchołki F i G należą do ramion trójkąta. W tym prostokącie |DE|:|EF|=6:1. Oblicz długości boków tego prostokąta.
W trójkąt ostrokątny ABC, w którym |AB|=8 oraz wysokość |CH|=6, wpisano kwadrat DEFG tak, że bok DE jest zawarty w boku AB, a wierzchołki F i G należą do boków AC i BC. Oblicz pole tego kwadratu.
W trapezie ABCD, w którym AB || CD i |AB|=2|CD|, punkt O jest punktem wspólnym przekątnych trapezu. Oblicz stosunek pola trójkąta ABO do pola trapezu.
W trójkącie prostokątnym kotangens jednego z kątów ostrych jest równy 2. Oblicz stosunek promienia okręgu opisanego na tym trójkącie do promienia okręgu wpisanego w ten trójkąt.
Promień okręgu wpisanego w trójkąt prostokątny o obwodzie 40 cm jest równy 4 cm. Oblicz długość przeciwprostokątnej tego trójkąta.
W koło w pisano kwadrat, a następnie w ten kwadrat wpisano koło. Wartość bezwzględna różnicy pól tych kół jest równa 8π cm2. Oblicz pole kwadratu.
W trójkącie równoramiennym ramię o długości 30 cm jest nachylone do podstawy pod kątem, którego sinus jest równy 0,6. Oblicz odległość od środka koła wpisanego w ten trójkąt od wierzchołków podstawy.
W trójkącie prostokątnym wysokość poprowadzona z wierzchołka kąta prostego dzieli przeciwprostokątną na odcinki o długościach 24 cm i 48 cm. Oblicz promień okręgu wpisanego w ten trójkąt.
W trapezie równoramiennym podstawy mają długości 27 cm i 18 cm, a ramię tworzy z dłuższą podstawą kąt, którego cosinus jest równy 0,6. Oblicz odległości punktu przecięcia przekątnych tego trapezu od podstaw.
Podstawy trapezu mają długości 13 cm i 11 cm. Odcinek łączący środki ramion trapezu dzieli ten trapez na dwa czworokąty. Oblicz stosunek pól tych czworokątów.
W trapezie równoramiennym, który nie jest równoległobokiem, przekątna o długości 10 cm jest nachylona do podstawy pod kątem, którego tangens jest równy 0,5. Oblicz pole tego trapezu.
W trapezie równoramiennym ABCD, w którym AB || CD, przekątna AC ma długość 80 cm. Punkt O jest środkiem koła opisanego na tym trapezie i |<BOC|=80°. Oblicz pole tego trapezu. Wynik podaj w cm2 z zaokrągleniem do drugiego miejsca po przecinku.
Trapez równoramienny jest opisany na kole o promieniu 10 cm. Ramię tego trapezu tworzy z dłuższą podstawą kąt, którego cosinus jest równy 0,(2). Oblicz pole tego trapezu. Wynik podaj w cm2 z zaokrągleniem do drugiego miejsca po przecinku.
Dany jest zbiór wszystkich równoległoboków o obwodzie równym 80 cm i kącie ostrym o mierze 48°. Oblicz pole równoległoboku należącego do tego zbioru, który ma największe pole. Wynik podaj w cm2 z zaokrągleniem do drugiego miejsca po przecinku.
W trójkąt prostokątny ABC, w którym |<ACB|=90°, sin|<CAB|=
i |AB|=34 cm, wpisujemy prostokąt CDEF tak, że punkt D należy do boku AC, punkt E należy do boku AB punkt F należy do boku BC. Oblicz wymiary prostokąta o największym polu.W trójkąt równoramienny ABC, w którym |AC|=|BC|=12 i cos |<ABC|=0,(3), wpisujemy prostokąty tak, że jeden bok prostokąta zawarty jest w podstawie AB a dwa pozostałe wierzchołki należą do ramion trójkąta. Oblicz wymiary prostokąta o największym polu.
Dany jest prostokąt ABCD, w którym AB || CD, a przekątna AC o długości 26 cm tworzy z dłuższym bokiem kąt, którego sinus jest równy
. Punkt E należy do boku AB, punkt F należy do boku BC, punkt G należy do boku CD, punkt H należy do boku AD i |AE|=|BF|=|CG|=|DH|=x. Oblicz wartość x, dla której czworokąt EFGH ma najmniejsze pole.
Wyszukiwarka
Podobne podstrony:
Kombinatoryka - Zadania, Nauka, Matematyka, Kombinatoryka. Prawdopodobieństwo
zadania, Nauka, Matematyka
trygonometria - zadania z planimetrii, zadania z matematyki
DODAWANIE I ODEJMOWANIE W ZAKRESIE 100-zadania, Nauka pomoce, matematyka
zadania - algebra 1, nauka, matematyka, LICEUM, 1 KLASA, I RÓWNANIA I NIERÓWNOŚCI
zadania - symetria, nauka, matematyka, LICEUM, 2 KLASA, II FIGURY I PRZEKSZTAŁCENIA
zadania - pola figur 2, nauka, matematyka, LICEUM, 1 KLASA, II FIGURY GEOMETRYCZNE
zadania - logika, nauka, matematyka, LICEUM, 1 KLASA, LOGIKA
Matematyka finansowa - wzory i zadania-wydanie nowe, Nauka, Matematyka
zadania - pitagoras, nauka, matematyka, LICEUM, 1 KLASA, II FIGURY GEOMETRYCZNE
zadania - pola figur, nauka, matematyka, LICEUM, 1 KLASA, II FIGURY GEOMETRYCZNE
zadania - symetria 1, nauka, matematyka, LICEUM, 2 KLASA, II FIGURY I PRZEKSZTAŁCENIA
zadania - koło 1, nauka, matematyka, LICEUM, 2 KLASA, II FIGURY I PRZEKSZTAŁCENIA
zadania - koło, nauka, matematyka, LICEUM, 2 KLASA, II FIGURY I PRZEKSZTAŁCENIA
Zadania z planimetrii zadania z matemaks pl docx
Prostokątny Trójkąt Planimetria zadania z matematyki Zadania info, 464
(eBook PL,matura, kompedium, nauka ) Matematyka liczby i zbiory maturalne kompedium fragmid 1287
zadanie domowe matematyka, scenariusze
Zagadnienia obowiązujące do egz z logiki, Nauka, Matematyka
więcej podobnych podstron