POLITECHNIKA POZNAŃSKA INSTYTUT ELEKTROTECHNIKI PRZEMYSŁOWEJ Zakład Podstaw Elektrotechniki |
|||
Laboratorium Podstaw Elektrotechniki Ćwiczenie nr 6 Temat: Rezonans w obwodzie szeregowym |
|||
Rok akademicki: Wydział Elektryczny Studia dzienne magisterskie Nr grupy: E-5 |
Wykonawcy: 1. Paweł Matuszak 2. Szymon Matelski 3. Andrzej Melonek
|
Data |
|
|
|
Wykonania ćwiczenia |
Oddania sprawozdania |
|
|
02,12,2003
|
16,12,2003 |
|
|
Ocena: |
|
Uwagi:
|
|||
1. Wiadomości teoretyczne.
(pojęcie rezonansu, rezonans napięć, dobroć obwodu rezonansowego, pasmo przepuszczania, przepięcia rezonansowe, charakterystyki częstotliwościowe, rezonans fazowy i amplitudowy, przedstawić cel przeprowadzonego ćwiczenia).
Rezonansem napięć nazywamy taki stan obwodu szeregowego RLC, w którym impedancja obwodu ma charakter wyłącznie czynny. Zachodzi to wówczas, gdy: XL=XC. Równość obu reaktancji może być osiągnięta bądź drogą zmiany wartości elementów L, C, bądź też drogą zmiany częstotliwości źródła zasilającego. Nastąpi to dla tzw. „pulsacji rezonansowej”: ![]()
. Impedancja obwodu w stanie rezonansu osiąga wartość minimalną Z0=R, zaś prąd osiąga wartość maksymalną: ![]()
. Dobroć obwodu przy pulsacji rezonansowej wynosi: 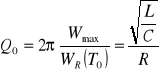
, gdzie: Wmax - największa wartość energii magazynowanej przy rezonansie w indukcyjności lub pojemności, WR(T0) - energia tracona w rezystancji obwodu w ciągu okresu T0.
Charakterystyki: 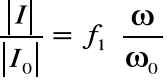
, 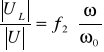
, 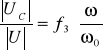
, nazywamy uniwersalnymi charakterystykami częstotliwościowymi obwodu szeregowego RLC. Można wykazać, że:
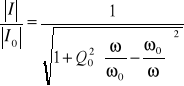
, 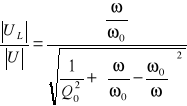
, 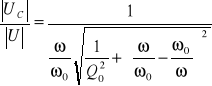
.
W stanie rezonansu, gdy: 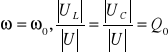
. Oznacza to, że w stanie rezonansu napięcia na indukcyjności
i pojemności są sobie równe i mogą znacznie przewyższyć wartość napięcia zasilającego. Jednakże wartości te nie są ekstremalne: wartość największa napięcia UL występuje przy pulsacji: 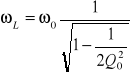
, czyli nieco powyżej pulsacji rezonansowej, a wartość największa napięcia UC występuje przy pulsacji: 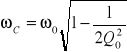
, czyli nieco poniżej pulsacji rezonansowej.
Zakres pulsacji (ω2- ω1) w pobliżu rezonansu, na którego granicach prąd względny ![]()
zmniejsza się do wartości ![]()
przyjęto nazywać pasmem przepuszczania obwodu rezonansowego. Można wykazać, że: ![]()
.
Za kryterium wystąpienia rezonansu przyjęto zgodność faz napięcia zasilającego i prądu. Jest to tzw. rezonans fazowy. Występująca równocześnie z nim wartość ekstremalna prądu, a więc tzw. rezonans amplitudowy ma miejsce tylko w przypadkach idealnych. W układzie rzeczywistym rezonans fazowy nie występuje równocześnie
z rezonansem amplitudowym, toteż znaczenie praktyczne omówionego obwodu zależy w dużym stopniu od tego, czy można go uważać za układ zastępczy obwodu rzeczywistego. Szeregowy obwód RLC jest dogodny jako układ zastępczy szeregowego połączenia rezystora, cewki i kondensatora. Uwzględnia on raczej straty w cewce niż straty
w kondensatorze, co jest dość dobrym przybliżeniem rzeczywistości, gdyż starty w kondensatorach obwodów rezonansowych są z reguły znacznie mniejsze niż straty w cewkach.
2. Przebieg ćwiczenia
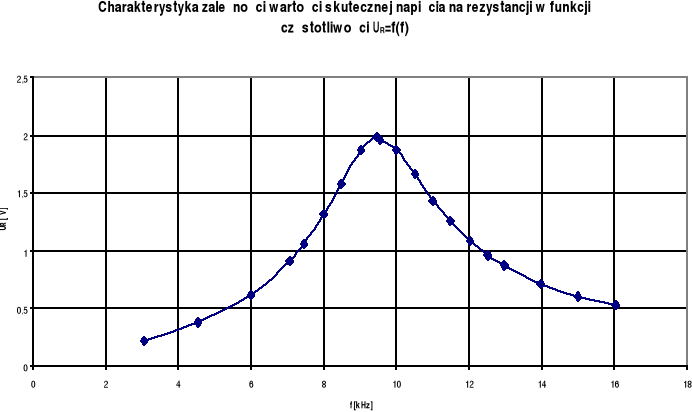
2.1. Wyznaczenie charakterystyki spadku napięcia na rezystancji (prądu) w funkcji częstotliwości.
2.1.1. Schemat połączeń
Dane:U=2,0 [V], R=1000 [Ω], L=56 [mH], C=5060 [pF]
2.1.2. Przebieg pomiarów
Zestawilismy układ przedstawiony w punkcie 2.1.1. Poszukaliśmy taką częstotliwość generatora, aby wystąpił maksymalny spadek napięcia na rezystancji. Następnie dokonaliśmy pomiarów napięcia na rezystancji przy częstotliwościach niższych i wyższych, utrzymując stałą wartość napięcia generatora. Wyniki pomiarów zamieściliśmy w tabeli 2.1.3.
2.1.3. Tabela wyników pomiarów
Lp |
f |
UR |
|
[kHz] |
[V] |
1 |
3,070 |
0,222 |
2 |
4,555 |
0,381 |
3 |
5,991 |
0,620 |
4 |
7,066 |
0,915 |
5 |
7,449 |
1,061 |
6 |
8,014 |
1,322 |
7 |
8,496 |
1,577 |
8 |
9,019 |
1,868 |
9 |
9,457 |
1,981 |
10 |
9,534 |
1,962 |
11 |
9,999 |
1,875 |
12 |
10,52 |
1,665 |
13 |
11,00 |
1,431 |
14 |
11,47 |
1,261 |
15 |
12,02 |
1,078 |
16 |
12,53 |
0,957 |
17 |
12,97 |
0,871 |
18 |
13,97 |
0,711 |
19 |
15,01 |
0,603 |
20 |
16,03 |
0,524 |
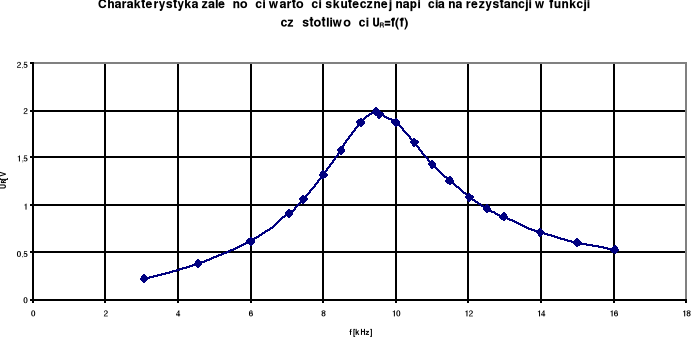
Wykreśliliśmy charakterystykę zależności wartości skutecznej napięcia na rezystancji w funkcji częstotliwości UR=f(f).
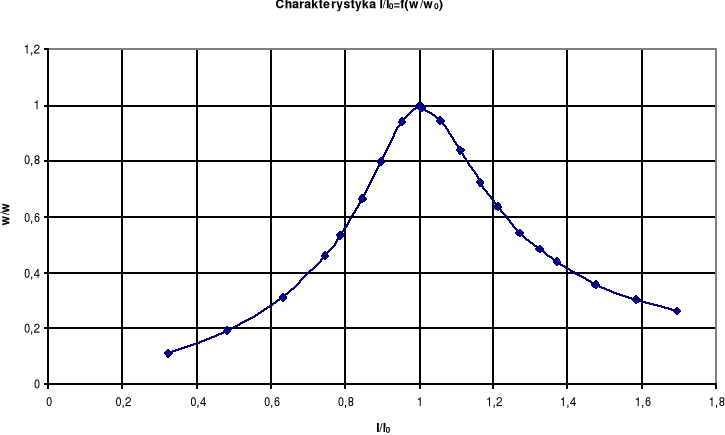
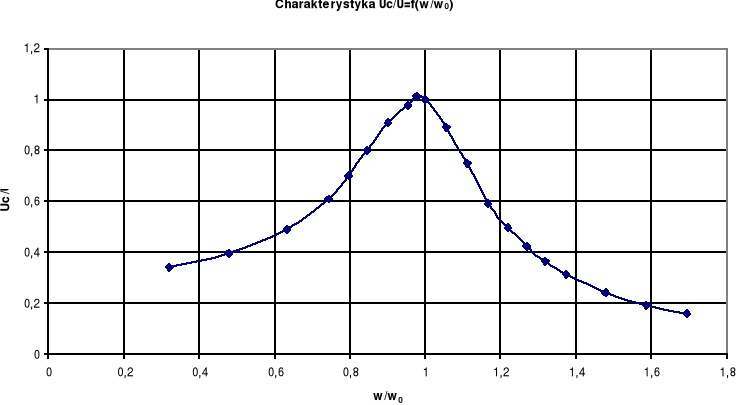
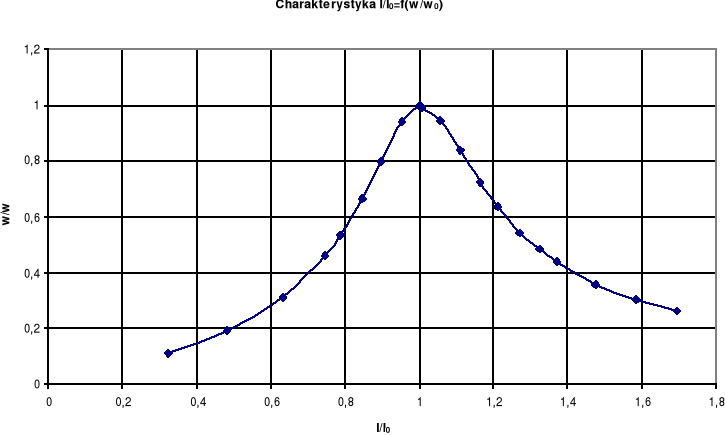
2.1.4. Zestawienie wyników obliczeń.
Wykonaliśmy odpowiednie obliczenia, zestawiliśmy je w poniższej tabeli i sporządziliśmy charakterystykę: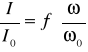
Lp |
ω/ ω 0 |
I/I0 |
1 |
0,325 |
0,112 |
2 |
0,482 |
0,192 |
3 |
0,633 |
0,313 |
4 |
0,747 |
0,462 |
5 |
0,788 |
0,536 |
6 |
0,847 |
0,667 |
7 |
0,898 |
0,796 |
8 |
0,954 |
0,943 |
9 |
1 |
1 |
10 |
1,008 |
0,99 |
11 |
1,057 |
0,946 |
12 |
1,112 |
0,84 |
13 |
1,163 |
0,722 |
14 |
1,213 |
0,637 |
15 |
1,271 |
0,544 |
16 |
1,325 |
0,483 |
17 |
1,371 |
0,44 |
18 |
1,477 |
0,359 |
19 |
1,587 |
0,304 |
20 |
1,695 |
0,265 |
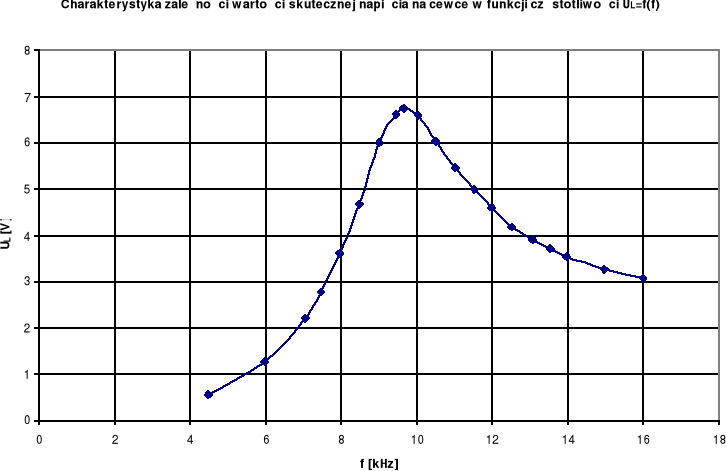
2.2. Wyznaczenie charakterystyki napięcia na cewce w funkcji częstotliwości
2.2.1. Schemat połączeń
Dane: U=2,0 [V], R=1000 [Ω], L=56 [mH], C=5060 [pF]
2.2.2. Przebieg pomiarów
Zestawiliśmy układ przedstawiony w punkcie 2.2.1. Poszukaliśmy taką częstotliwość generatora, aby wystąpił maksymalny spadek napięcia na cewce. Następnie dokonaliśmy pomiarów napięcia na cewce przy częstotliwościach niższych i wyższych, utrzymując stałą wartość napięcia generatora. Wyniki pomiarów zamieściliśmy w tabeli 2.2.3.
2.2.3. Tabela wyników pomiarów
Lp |
f |
UL |
|
[kHz] |
[V] |
1 |
4,485 |
0,574 |
2 |
5,995 |
1,286 |
3 |
7,046 |
2,220 |
4 |
7,477 |
2,785 |
5 |
7,971 |
3,611 |
6 |
8,500 |
4,685 |
7 |
9,016 |
6,003 |
8 |
9,450 |
6,620 |
9 |
9,670 |
6,740 |
10 |
10,03 |
6,605 |
11 |
10,51 |
6,028 |
12 |
11,04 |
5,468 |
13 |
11,52 |
4,996 |
14 |
11,99 |
4,606 |
15 |
12,52 |
4,193 |
16 |
13,06 |
3,914 |
17 |
13,53 |
3,713 |
18 |
13,98 |
3,550 |
19 |
14,98 |
3,272 |
20 |
15,99 |
3,068 |
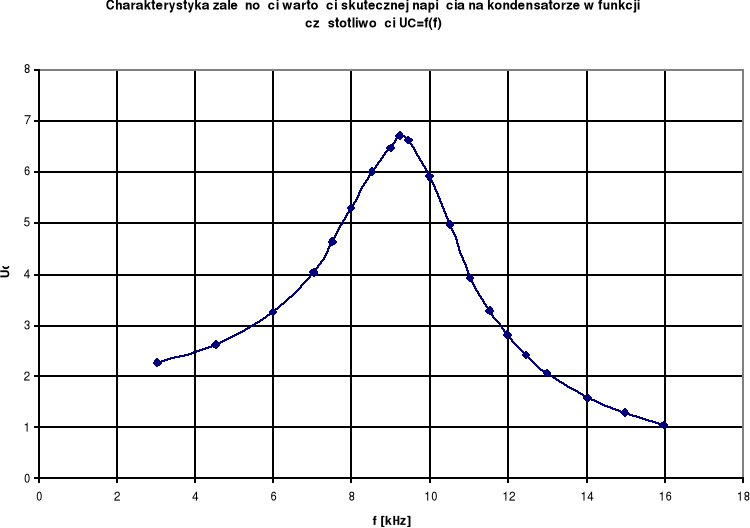
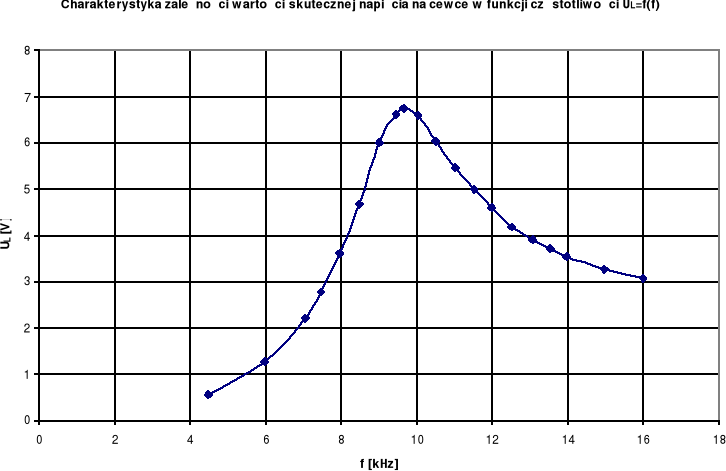
Wykreśliliśmy charakterystykę zależności wartości skutecznej napięcia na cewce w funkcji częstotliwości UL=f(f).
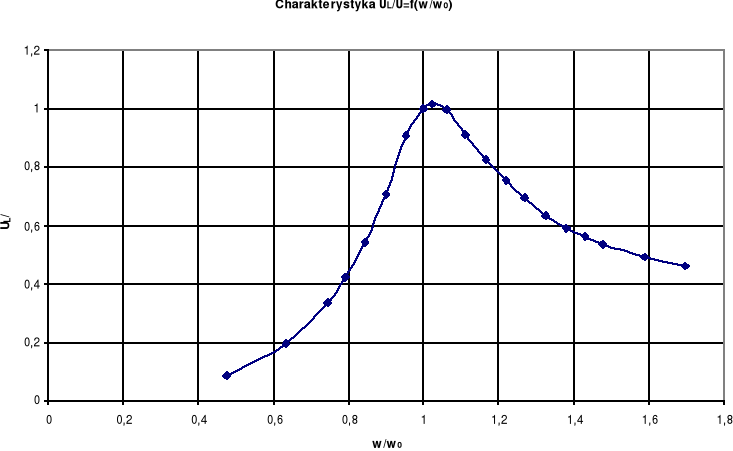
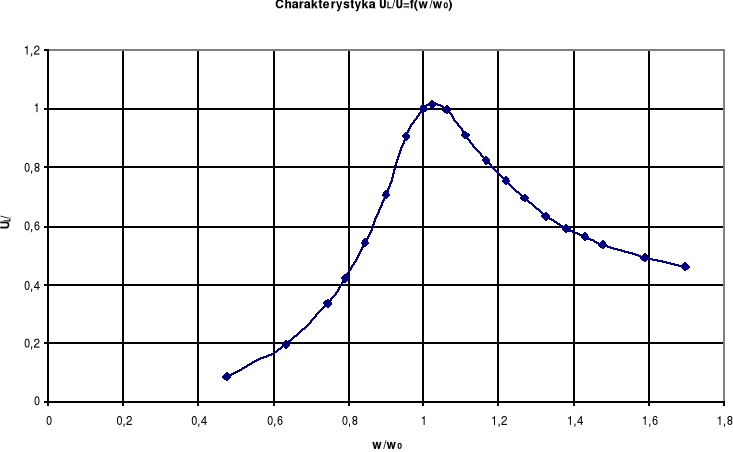
2.2.4. Zestawienie wyników obliczeń.
Wykonaliśmy odpowiednie obliczenia i zestawiliśmy je w poniższej tabeli, a potem sporządziliśmy charakterystykę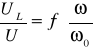
Lp |
ω / ω 0 |
UL/U |
1 |
0,475 |
0,087 |
2 |
0,634 |
0,194 |
3 |
0,746 |
0,335 |
4 |
0,791 |
0,421 |
5 |
0,843 |
0,545 |
6 |
0,899 |
0,708 |
7 |
0,954 |
0,907 |
8 |
1 |
1 |
9 |
1,023 |
1,018 |
10 |
1,061 |
0,998 |
11 |
1,112 |
0,911 |
12 |
1,168 |
0,826 |
13 |
1,219 |
0,755 |
14 |
1,269 |
0,696 |
15 |
1,325 |
0,633 |
16 |
1,382 |
0,591 |
17 |
1,432 |
0,561 |
18 |
1,478 |
0,536 |
19 |
1,588 |
0,494 |
20 |
1,696 |
0,463 |
2.3. Wyznaczenie charakterystyki napięcia na kondensatorze w funkcji częstotliwości
2.3.1. Schemat połączeń
Dane: U=2,0 [V], R=1000 [Ω], L=56 [mH], C=5060 [pF]
2.3.2. Przebieg pomiarów
Zestawiliśmy układ przedstawiony w punkcie 2.3.1. Poszukaliśmy taką częstotliwość generatora, aby wystąpił maksymalny spadek napięcia na kondensatorze. Następnie dokonaliśmy pomiarów napięcia na kondensatorze przy częstotliwościach niższych i wyższych, utrzymując stałą wartość napięcia generatora. Wyniki pomiarów zamieściliśmy w tabeli 2.3.3.
2.3.3. Tabela wyników pomiarów
Lp |
f |
UC |
|
[kHz] |
[V] |
1 |
3,034 |
2,271 |
2 |
4,520 |
2,613 |
3 |
5,992 |
3,247 |
4 |
7,030 |
4,030 |
5 |
7,522 |
4,642 |
6 |
7,984 |
5,290 |
7 |
8,515 |
6,015 |
8 |
9,010 |
6,478 |
9 |
9,235 |
6,721 |
10 |
9,450 |
6,620 |
11 |
9,981 |
5,910 |
12 |
10,51 |
4,964 |
13 |
11,03 |
3,926 |
14 |
11,52 |
3,288 |
15 |
11,99 |
2,805 |
16 |
12,47 |
2,409 |
17 |
12,99 |
2,070 |
18 |
14,03 |
1,580 |
19 |
14,98 |
1,276 |
20 |
15,98 |
1,049 |
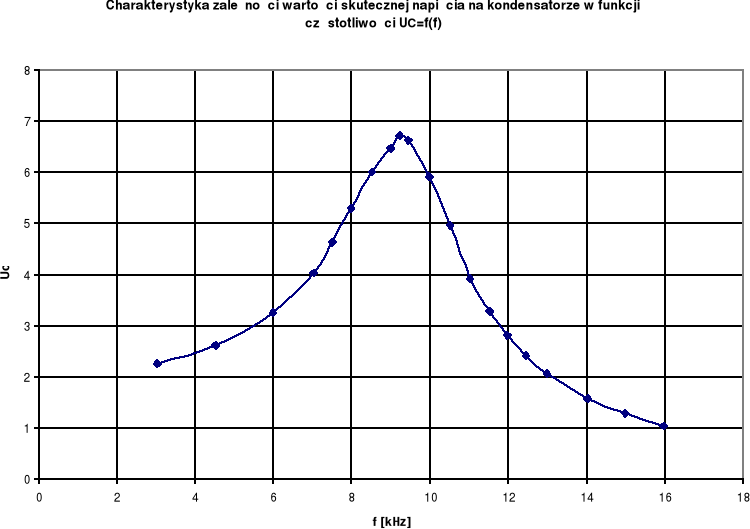
Wykreśliliśmy charakterystykę zależności wartości skutecznej napięcia na kondensatorze w funkcji częstotliwości UC=f(f).
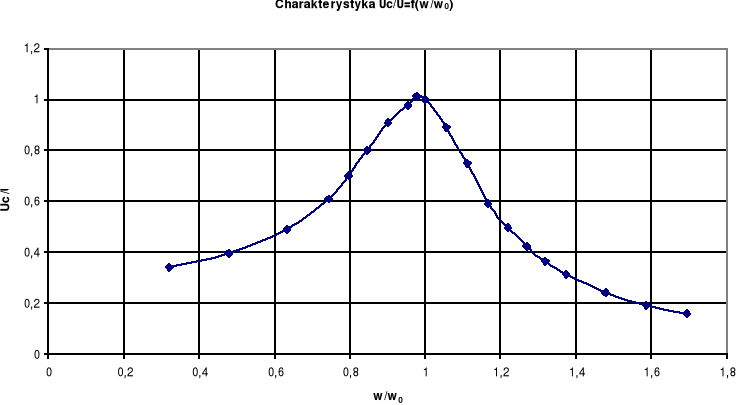
2.3.4. Zestawienie wyników obliczeń.
Wykonaliśmy odpowiednie obliczenia i zestawiliśmy je w poniższej tabeli, a następnie sporządziliśmy charakterystykę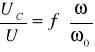
.
Lp |
ω / ω 0 |
UC/U |
1 |
0,321 |
0,343 |
2 |
0,478 |
0,395 |
3 |
0,634 |
0,490 |
4 |
0,744 |
0,609 |
5 |
0,796 |
0,701 |
6 |
0,845 |
0,799 |
7 |
0,901 |
0,909 |
8 |
0,953 |
0,979 |
9 |
0,977 |
1,015 |
10 |
1 |
1 |
11 |
1,056 |
0,893 |
12 |
1,112 |
0,750 |
13 |
1,167 |
0,593 |
14 |
1,219 |
0,497 |
15 |
1,269 |
0,424 |
16 |
1,32 |
0,364 |
17 |
1,375 |
0,313 |
18 |
1,478 |
0,239 |
19 |
1,588 |
0,193 |
20 |
1,696 |
0,158 |
3. Obliczenia
3.1. Z danych parametrów wyznaczyć:
a) pulsację rezonansową
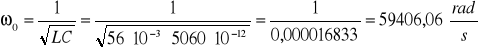
częstotliwość rezonansową
![]()
dobroć obwodu przy pulsacji rezonansowej
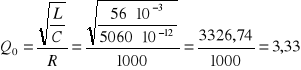
dobroć cewki i kondensatora przy pulsacji rezonansowej
![]()
![]()
3.2. Narysować charakterystyki UR, UL, UC w funkcji częstotliwości dla układu szeregowego (na jednym wykresie).
3.3. Z charakterystyki przebiegu napięcia na rezystancji UR=f(f) wyznaczyć dobroć obwodu rezonansowego Q0.
3.4. Z charakterystyk przebiegu napięć na cewce i kondensatorze (UL,UC=f(f)) wyznaczyć dobroć obwodu rezonansowego.
3.5. Wykreślić charakterystyki: R, XL, XC, Z, XL -XC=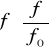
.
4. Parametry i dane zmianowe zastosowanych urządzeń i mierników.
Generator MOTECH FG-506.
Płytka do badania rezonansu szeregowego.
Dwa mierniki uniwersalne BRYMEN BM 857
5. Uwagi końcowe i wnioski.
Celem ćwiczenia było zbadanie własności szeregowego obwodu rezonansowego RLC zasilanego ze źródła napięcia.
Wyszukiwarka
Podobne podstrony:
Rezonans (Owca), Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 06. Rezonans
Rezonans w obwodzie szeregowym tabela pomiarowa, Politechnika Poznańska, Elektrotechnika, Teoria obw
Rezonans w obwodzie szeregowym - brudnopis, Politechnika Poznańska, Elektrotechnika, Teoria obwodów,
Rezonans w obwodzie równoległym, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratori
Twierdzenie Tevenina i Nortona Bob (3), Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Lab
Twierdzenie Tevenina i Nortona Bob (1), Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Lab
Tabelka ćw 4, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 04. Poprawianie
cw3teor, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 03. Źródło rzeczywist
Wygładzanie tętnień prądu - wykresy - Maciek, Politechnika Poznańska, Elektrotechnika, Teoria obwodó
Układy trójfazowe niesymetryczne - j, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Labor
Poprawa współczynnika mocy, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 04
Thevenin (Tomaj), Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 02. Twierdze
stany nieustalone, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 12. Stany n
Poprawianie współczynnika mocy, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria
czworniki (Daniel3), Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 08. Czwór
moc maxymalna beta, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 03. Źródło
Twierdzenie Thevenina i Nortona - W, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Labora
czwórniki - matej, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 08. Czwórni
Czwórniki równoważne - a, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 08.
więcej podobnych podstron