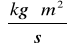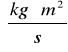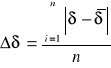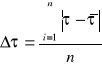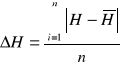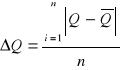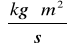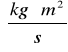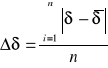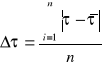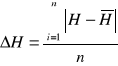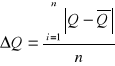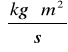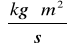r. akad. 00/01
|
L A B O R A T O R I U M Z F I Z Y K I
|
|||
nr ćwicz. 25 |
Rezonans mechaniczny |
|||
wydział: Mechaniczny R02 grupa: R02 |
imię i nazwisko: Marcn Kasprzyk |
|||
data wykonania: |
ocena |
data zaliczenia |
podpis |
|
|
teoria |
|
|
|
|
Sprawozdanie |
|
|
|
1. Zasada pomiaru
Celem ćwiczenia jest zapoznanie się z ruchem drgającym tłumionym, drganiami wymuszonymi i rezonansem drgań. A także wyznaczenie dekrementu logarytmicznego tłumienia, czasu relaksacji, współczynnika oporu oraz dobroci układu drgań tłumionych.
Drgania tłumione są drganiami o zmniejszającej się amplitudzie. Gdy na układ podziałamy siłą zmieniającą się okresowo, na przykład siła sinsoidalnie zmienną, wówczas ustalą się drgania o stałej amplitudzie, czyli niegasnące. Nazywamy je drganiami wymuszonymi.
Wielkości charakteryzujące ruch drgań tłumionych:
1. Dekrement logarytmiczny tłumienia
![]()
gdzie n to ilość drgań,
lub
Przy czym: T - okres drgań tłumionych; β- współczynnik tłumienia.
2. Czas relaksacji - τ- to czas, w którym amplituda drgań zmaleje e razy w stosunku do swej wartości początkowej,
![]()
3. Dobroć obwodu, która równa jest iloczynowi 2π i ilorazu energii oscylatora przez średnią energię traconą w jednym cyklu.
Można pokazać, że:
4. Współczynnik tłumienia
gdzie H - Współczynnik oporu ; I - moment bezwładności.
W doświadczeniu mamy również do czynienia z drganiami wymuszonymi.
Mw = M0 ∗ cos ωt
Przy czym: Mo - amplituda momentu wymuszającego; ω - częstość kołowa momentu wymuszającego.
Amplituda drgań jest największa w czasie gdy występuje rezonans. Rezonans mechaniczny występuje gdy impulsy działają na układ z częstotliwością w przybliżeniu równą częstotliwości drgań własnych pobudzanego układu.
Dobroć obwodu można odczytać wykresu krzywej rezonansowej i jest ona równa stosunkowi częstości rezonansowej układu do połówkowej szerokości krzywej rezonansu.
2. Ocena dokładności pojedynczych pomiarów.
W doświadczeniu stosowano następujące urządzenia :
- amperomierz (zkres 3000 mA; klasa dokładności 0,5),
- zasilacz regulowany 0 - 25 V,
- stoper.
Błąd odczytu amplitudy drgań przyjęto:
ΔA=0,5 najmniejszej działki na skali = 0,25 działki.
Błąd stopera przyjęto Δt = 0,5 s.
Błąd natężenia prądu ΔI 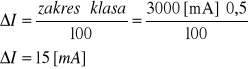
3. Tabele pomiarowe
TABELA 1
Wyznaczanie wielkości charakteryzujących swobodne drgania gasnące.
Lp |
Ao [dz] |
A4 [dz] |
t4 [s] |
T [s] |
δ |
|
τ [s] |
[s] |
H
|
|
Q |
|
1. 2. 3. 4. 5. |
5 6 7 8 9 |
3 4 5 5,5 6 |
5,53 5,60 5,37 5,22 5,72 |
1,38 1,40 1,34 1,31 1,43 |
0,13 0,10 0,08 0,09 0,10 |
0,03 0,00 0,02 0,01 0,00 |
10,62 14,00 16,75 14,56 14,30 |
3,43 0,05 2,70 0,51 0,25 |
6,59 5,00 4,18 4,81 4,90 |
1,49 0,10 0,92 0,29 0,20 |
48,35 62,83 78,54 69,83 62,83 |
16,13 1,65 14,06 5,35 1,65 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
0,06 |
14,05 |
6,94 |
5,10 |
3,00 |
64,48 |
38,84 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
0,012 |
1,39 |
0,60 |
7,80 |
||||
TABELA 1a I = 1,2 [A]
Lp |
Ao [dz] |
An [dz] |
t4 [s] |
T [s] |
δ |
|
τ [s] |
[s] |
H
|
|
Q |
|
1. 2. 3. 4. 5. |
5 6 7 8 9 |
2 2,5 3 3,5 4,5 |
5,50 5,41 5,75 5,41 5,43 |
1,38 1,35 1,44 1,35 1,36 |
0,23 0,22 0,21 0,21 0,17 |
0,02 0,01 0,00 0,00 0,04 |
6,00 6,14 6,86 6,43 8,00 |
0,69 0,55 0,17 0,26 1,31 |
11,67 11,40 10,20 10,89 8,75 |
1,09 0,82 0,38 0,31 1,83 |
27,32 28,58 29,93 29,93 36,96 |
3,22 1,96 0,61 0,61 6,42 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,21 |
0,07 |
6,69 |
2,98 |
10,58 |
4,43 |
30,54 |
12,82 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
0,014 |
0,60 |
0,89 |
2,56 |
||||
TABELA 2
Wyznaczanie krzywej rezonansu.
A |
[dz] |
1 |
2,5 |
4 |
6,5 |
9 |
7 |
2,5 |
1,5 |
0,5 |
T10 |
[s] |
27,9 |
17,10 |
15,79 |
14,53 |
13,81 |
13,03 |
11,97 |
10,94 |
8,22 |
T |
[s] |
2,79 |
1,71 |
1,58 |
1,45 |
1,38 |
1,30 |
1,20 |
1,09 |
0,82 |
Ω |
|
2,25 |
3,67 |
3,98 |
4,33 |
4,55 |
4,83 |
5,24 |
5,76 |
7,66 |
4. Przykładowe obliczenia wyników pomiarów wielkości złożonej
a) obliczenie okresu drgań T dla pomiaru nr 1 z tabeli 1:
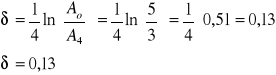
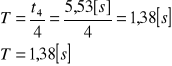
b) wyznaczenie wartości logarytmicznego dekrementu tłumienia δ dla pomiaru nr 1 z tabeli 1:
c) obliczenie czasu ralaksacji τ dla pomiaru nr 1 z tabeli 1:
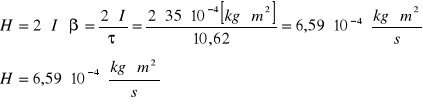
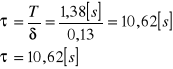
d) obliczenie współczynnika oporu H dla pomiaru nr 1 z tabel 1:
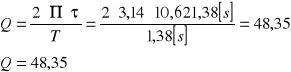
e) obliczenie dobroci Q układu dla pomiaru nr 1 z tabeli 1:
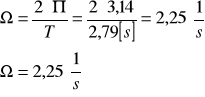
f) wyznaczenie częstości kołowej drgań Ω dla pomiaru nr 1 z tabeli 2:
5. Rachunek błędów
wyznaczenie błędu ΔT dla pomiaru nr 1 z tabeli 1 ze wzoru:
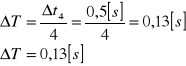
wyznaczenie błędu przeciętnego Δδp dla pomiaru nr 1 z tabeli 1:
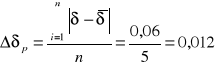
wyznaczenie błędu logarytmicznego dekrementu tłumienia metodą różniczki logarytmicznej:
![]()
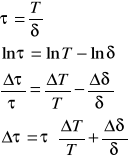
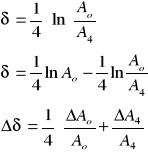
- dla danych zawartych w tabeli 1 pozycja nr 1:
wyznaczenie błędu czasu relaksacji metodą różniczki logarytmicznej:
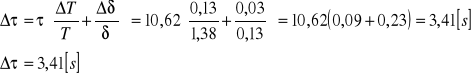
dla danych zawartych w tabeli 1 pozycja nr 1:
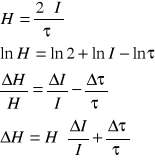
wyznaczenie błędu współczynnika oporu metodą różniczki logarytmicznej:
dla danych zawartych w tabeli 1 pozycja nr 1:
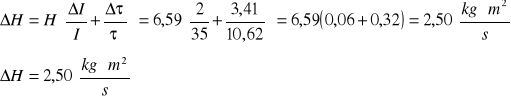
wyznaczenie błędu dobroci układu metodą różniczki logarytmicznej:
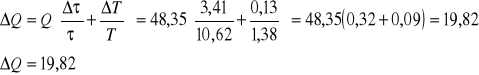
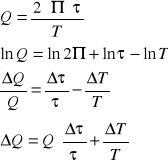
- dla danych zawartych w tabeli 1 pozycja nr 1:
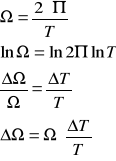
wyznaczenie błędu częstości kołowej drgań metodą różniczki logarytmicznej:
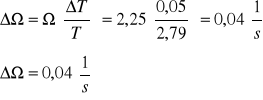
dla danych zawartych w tabeli 2 pozycja nr 1
Z wykresu odczytujemy częstość rezonansową równą 4,55 Hz, oraz szerokość krzywej rezonansu (0,4 Błąd! Nie określono zakładki.0,15)Hz. Dobroć układu obliczamy ze wzoru:
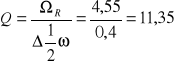
6. Zestawienie wyników pomiarowych
DOŚWIADCZENIE I
I = 0 [A]
Pomiar |
1 |
2 |
3 |
4 |
5 |
Ao [dz] |
5,00 ± 0,25 |
6,00 ± 0,25 |
7,00 ± 0,25 |
8,00 ± 0,25 |
9,00 ± 0,25 |
A4 [dz] |
3,00 ± 0,25 |
4,00 ± 0,25 |
5,00 ± 0,25 |
5,50 ± 0,25 |
6,00 ± 0,25 |
T [s] |
1,38 ± 0,13 |
1,40 ± 0,13 |
1,34 ± 0,13 |
1,31 ± 0,13 |
1,43 ± 0,13 |
δ |
0,13 ± 0,03 |
0,10 ± 0,03 |
0,08 ± 0,03 |
0,09 ± 0,02 |
0,10 ± 0,02 |
τ [s] |
10,62 ± 3,41 |
14,00 ± 5,46 |
16,75 ± 7,96 |
14,56 ± 4,69 |
14,30 ± 4,15 |
H |
6,59 ± 2,50 |
5,00 ± 2,25 |
4,18 ± 2,26 |
4,81 ± 1,83 |
4,90 ± 1,72 |
Q [dz] |
48,35 ± 19,82 |
62,83 ± 30,16 |
78,54 ± 45,55 |
69,83 ± 29,93 |
62,83 ± 23,88 |
I = 1,2 [A]
Pomiar |
1 |
2 |
3 |
4 |
5 |
Ao [dz] |
5,00 ± 0,25 |
6,00 ± 0,25 |
7,00 ± 0,25 |
8,00 ± 0,25 |
9,00 ± 0,25 |
A4 [dz] |
2,00 ± 0,25 |
2,50 ± 0,25 |
3,00 ± 0,25 |
3,50 ± 0,25 |
4,50 ± 0,25 |
T [s] |
1,38 ± 0,13 |
1,35 ± 0,13 |
1,44 ± 0,13 |
1,35 ± 0,13 |
1,36 ± 0,13 |
δ |
0,23 ± 0,04 |
0,22 ± 0,04 |
0,21 ± 0,03 |
0,21 ± 0,03 |
0,17 ± 0,02 |
τ [s] |
6,00 ± 1,58 |
6,14 ± 1,73 |
6,86 ± 1,58 |
6,43 ± 1,54 |
8,00 ± 1,76 |
H |
6,59 ± 3,73 |
5,00 ± 3,88 |
4,18 ± 2,96 |
4,81 ± 3,27 |
4,90 ± 2,45 |
Q |
27,32 ± 9,56 |
28,58 ± 10,86 |
29,93 ± 9,58 |
29,93 ± 10,18 |
36,96 ± 11,83 |
DOŚWIADCZENIE II
A [dz] |
Ω |
1,0±0,25 |
2,25±0,04 |
2,5±0,25 |
3,67±0,11 |
4,0±0,25 |
3,98±0,13 |
6,5±0,25 |
4,33±0,15 |
9,0±0,25 |
4,55±0,16 |
7,0±0,25 |
4,83±0,19 |
2,5±0,25 |
5,24±0,22 |
1,5±0,25 |
5,76±0,26 |
0,5±0,25 |
7,66±0,47 |
8. Uwagi i wnioski
Zmieniając natężenie prądu w obwodzie z elektromagnesem, zmieniano tłumienie. Z otrzymanych wyników pomiarowych widać, że dla mniejszego tłumienia czas relaksacji jest większy. Jest to zgodne z intuicją, gdyż potrzeba więcej czasu, aby amplituda drgań zmieniła się e-razy.
Logarytmiczny dekrement tłumienia był z kolei dla tego przypadku mniejszy, gdyż stosunek dwóch kolejnych amplitud (w przypadku braku tłumienia) był mniejszy. Błąd logarytmicznego dekrementu tłumienia jest dość duży, dochodzi nawet do 37,5%. Związane jest to z małą dokładnością odczytu wyników pomiarowych ze skali na urządzeniu. Jako błąd odczytu przyjęto 0,5 działki jest to dość dużo gdyż przy odczycie ze skali wychylenia równego 1 otrzymujemy aż 25% błędu. Przy większych wychyleniach tarczy procentowy udział błędu jest znacznie mniejszy.
Zjawisko rezonansu ma olbrzymie znaczenie w życiu codziennym, znane są przypadki zniszczenia konstrukcji mostów przez nieznaczne siły zewnętrzne, na przykład rytmiczne podmuchy wiatru, ale o częstotliwości bliskiej częstotliwości drgań własnych tej konstrukcji.
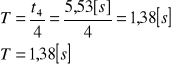
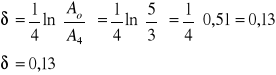
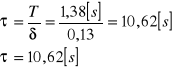
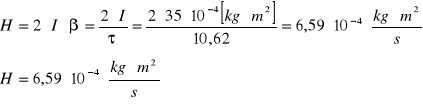
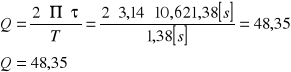
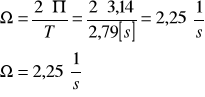
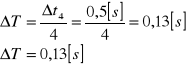
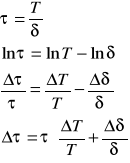
![]()
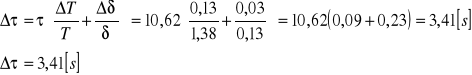
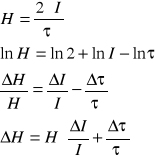
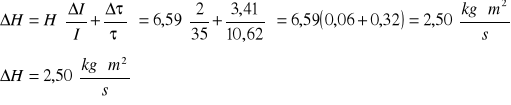
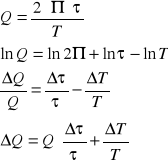
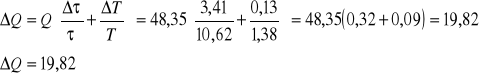
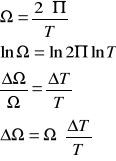
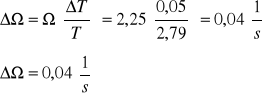
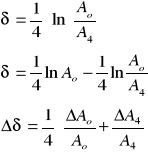
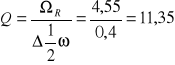
Wyszukiwarka
Podobne podstrony:
2LAB, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, sprawka od Mateusza, Fizyka -
C7, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, sprawka od Mateusza, Fizyka - la
C 47, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, sprawka od Mateusza, Fizyka -
Cw.47-Charakterystyka fotoogniwa1, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, s
41LAB-bez sensu, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, sprawka od Mateusza
Fiza 55 dzika, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, sprawka od Mateusza,
Cw.3 Równia pochyła, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, sprawka od Mate
Wykres zaleznosci I, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, sprawka od Mate
CW.1-Wyznaczenie przyspieszenia ziemskiego wahadla, 1 STUDIA - Informatyka Politechnika Koszalińska,
C27M, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, sprawka od Mateusza, Fizyka -
więcej podobnych podstron