1.Własności mechaniczne stali
Właściwości mechaniczne stali, podstawowe przy ocenie jej przydatności dla projektowanego elementu konstrukcyjnego, wynikają z procesu technologicznego, składu chemicznego stali oraz sposobu obróbki: mechanicznej, cieplnej i cieplno-chemicznej, a dla ich określenia wymagane jest prowadzenie badań wytrzymałościowych stali różnych gatunków.
Badania dotyczą następujących podstawowych właściwości mechanicznych stali: wytrzymałości na rozciąganie, granicy sprężystości i granicy plastyczności, udarności, wytrzymałości zmęczeniowej i twardości. Te wszystkie cechy dość dobrze charakteryzują jakość stali i pozwalają przewidywać, jak będzie się zachowywała ta stal w warunkach pracy z określonym obciążeniem
W przedziale wzmocnienia wydłużenia są stosunkowo duże przy względnie niewielkim przyroście obciążeń. Maksimum krzywej σ-ε w tym przedziale oznacza yt unitę
Wytrzymałości na rozciąganie Rm,jest jedną z podstawowych cech mechanicznych, charakteryzujących poszczególne gatunki stali. Określana ona wielkością naprężenia wywołanego w przekroju próbki przez siłę powodującą jej zerwanie. Po przekroczeniu granicy Rm w stali zaczyna formować się przewężenie i wkrótce następuje zerwanie.
Granicy sprężystości Re, która określa graniczną wartość naprężenia, przy którym jeszcze nie powstają makroskopowe odkształcenia materiału. Granica sprężystości ogranicza obszar odkształceń sprężystych, przy naprężeniach większych powstają bowiem wyraźne trwałe odkształcenia próbki. Umowną granicę sprężystości Re określa się jako naprężenie, wywołujące odkształcenie trwałe równe 0,05% pierwotnej długości pomiarowej próbki. Po przekroczeniu granicy Re osiąga się obszar odkształceń sprężysto-plastycznych.
Granica plastyczności Re tj. początek plastycznej fazy pracy materiału (odkształcenie trwałe epi = 0,13 -r 4%). Nagłe zmiany w równowadze na granicach ziarn przejawiają się nagłym wzrostem odkształcenia, co znajduje odzwierciedlenie na wykresie σ-ε w postaci tzw. przystanku plastycznego względnie półki plastycznej. W stalach o wysokiej wytrzymałości lub utwardzonych trudno jest uchwycić granicę Re, gdyż wykres wykazuje jedynie łagodne zaokrąglenie. W tych przypadkach za umowną granicę plastyczności Re przyjmuje się naprężenie odpowiadające wydłużeniu trwałemu 0,2%.
Udarność stali jest to zdolność jej do przenoszenia obciążeń pod uderzeniem. Udarność mierzy się pracą potrzebną do złamania jednym uderzeniem młota Charpey'ego. Praca ta jest miarą odporności stali na odkształcenia nagłe oraz miarą jej kruchości. Odporność na uderzenia zwiększa się im struktura stali jest drobnoziarnista i bardziej równomierna.
Twardość stali to opór z jakim przeciwstawia się ona wgniataniu bardzo twardego ciała obcego, wywierającego nacisk na bardzo małą powierzchnię. Twardość wzrasta wraz ze wzrostem zawartości węgla, manganu, niklu, chromu i wolframu.
Ciągliwość jest to właściwość pozwalająca na gięcie, prostowanie, spęcznianie i tym podobne formowanie stali na zimno, bez zniszczenia lub uszkodzenia. Ciągliwość sprawdza się, ustalając wydłużenie w % oraz wykonując próbę na zginanie i spęcznianie na zimno.
Kujność jest to właściwość pozwalająca na dowolne formowanie stali w temperaturze białego żaru, bez szkody dla wytrzymałości. Kujność stali obniża się wraz ze wzrostem zawartości węgla
2.Statyczna próba rozciągania stali, wykres σ-ε.
Próba statyczna rozciągania stali, służąca do określenia jej właściwości, jest przeprowadzana na próbkach okrągłych i płaskich z główkami, przy obciążeniu jednokierunkowym, równomiernie rozłożonym na przekroju próbki. Próbki wycina się na zimno, aby uniknąć zmiany struktury materiału.
Próbki powinny być przygotowane zgodnie z obowiązującymi normami jako krótkie pięciokrotne lub długie dziesięciokrotne.
Próbki rozciąga się w maszynie wytrzymałościowej aż do zerwania, zapisując jednocześnie zależność między odkształceniami a naprężeniami. Krzywa σ-ε ma kilka charakterystycznych punktów. Początkowo wydłużenia się proporcjonalne do naprężeń. Punki końcowy odcinka proporcjonalności to granica proporcjonalności RH. W tym przedziale ważne jest prawo Hookc'a, wyrażające się zależnością σ/ε=E=tg α = const.
Dla celów praktycznych wprowadza się pojęcie granicy sprężystości Re, która określa graniczną wartość naprężenia, przy którym jeszcze nie powstają makroskopowe odkształcenia materiału. Granica sprężystości ogranicza obszar odkształceń sprężystych, przy naprężeniach większych powstają bowiem wyraźne trwałe odkształcenia próbki. W technice umowną granicę sprężystości Re określa się jako naprężenie, wywołujące odkształcenie trwałe równe 0,05% pierwotnej długości pomiarowej próbki.
Po przekroczeniu granicy Re osiąga się obszar odkształceń sprężysto-plastycz-nych, gdzie współczynnik sprężystości podłużnej E ma zmienną wartość.
Nagłe zmiany w równowadze na granicach ziarn przejawiają się nagłym wzrostem odkształcenia, co znajduje odzwierciedlenie na wykresie w postaci tzw. przystanku plastycznego względnie półki plastycznej. Wtedy osiągnięta jest granica plastyczności Re tj. początek plastycznej fazy pracy materiału (odkształcenie trwałe epi = 0,13 - 4%).
W przypadku stali węglowych następuje skokowe przejście do zakresu większych odkształceń trwałych. Po osiągnięciu górnej granicy plastyczności ReH można zauważyć nagły spadek naprężeń do wartości dolnej granicy plastyczności Red.
W stalach o wysokiej wytrzymałości lub utwardzonych trudno jest uchwycić granicę Re, gdyż wykres wykazuje jedynie łagodne zaokrąglenie. W tych przypadkach za umowną granicę plastyczności Re przyjmuje się naprężenie odpowiadające wydłużeniu trwałemu 0,2%.
3.Nośność połączeń śrubowych zakładkowych i doczołowych
Kategorie połączeń.
W przypadku obciążeń zmiennych co do znaku zaleca się stosowanie połączeń sprężanych, pasowanych lub nitowanych, a w przypadku obciążeń dynamicznych (wielokrotnie zmiennych lub udarowych) - połączeń kategorii C i F, połączeń pasowanych, sprężanych lub nitowanych.
Kat. Poł.
|
A |
B |
C |
D |
E |
F |
||||||
Kier obc.
|
Prostopadły do osi łączników |
Równoległy do osi łączników |
||||||||||
Rodzaj połączenia |
zakładkowe |
doczołowe |
||||||||||
|
śrubowe 2) zwykłepasowane nitowe, sworz. |
sprężane 1) (cierne) |
niesprężane 3)lub sprężane 1) |
sprężane 1) |
||||||||
Stany graniczne I nośn. II użyt. |
I |
I |
II |
I |
I |
I |
II |
I |
||||
|
ścięcie lub docisk łączników |
poślizg styku |
zerwanie śrub |
rozwarcie styku |
||||||||
1) Do połączeń sprężanych należy stosować śruby o wysokiej wytrzymałości, tzn. klasy: 8.8, 10.9 lub 2) Połączenia na śruby o wysokiej wytrzymałości można projektować jako sprężane siła równą 0,5S0 = 0,35RmAs. 3) Do połączeń niesprężanych stosuje się śruby klas niższych niż 8.8. |
||||||||||||
Wymagania konstrukcyjne:
- całkowita grubość łączonych części (blach) powinna spełniać warunki:
∑t ≤5d - w połączeniach nitowych i śrubowych,
∑t ≤8d - w połączeniach śrubowych sprężonych,
d - średnica łącznika,
- w połączeniach zakładkowych łączniki należy rozmieszczać w układzie
prostokątnym lub przestawionym zgodnie z wymaganiami podanymi w
tablicy 8 ,
- w połączeniach doczołowych odległość śrub od swobodnej krawędzi
blachy powinna wynosić : 1,5d ≤ a2 ≤ 6t, a odległość miedzy śrubami
2,5d ≤ a ≤ 15t, gdzie t - grubość blachy czołowej.
układ prostokątny układ przestawny
Połączenia powinny mieć zapewnioną odpowiednią nośność, sztywność oraz zdolność do odkształceń plastycznych. Sumaryczna grubość łączonych części (blach) powinna spełniać warunki:
Σt =< 5d - w połączeniach nitowych i śrubowych, Σt =< 5d - w połączeniach śrubowych sprężonych. Średnice otworów na nity i sworznie zaleca się przyjmować o 1 mm większe niż średnica trzpienia. W połączeniach doczołowych odległość śrub od swobodnej krawędzi blachy powinna wynisić1,5 d =< a1 =< 6t między śrubami 2,5 d =< a =<15 t
Nośność trzpienia SR = min (SRb, SRV)
SRb - nośność na docisk; SRb = Ab fdb fdb = α fd
SRV - nośność na ścinanie. SRV = AV fdV
α = min ( a1/d, a/d - ¾, 2,5)
W przypadku połączeń obciążonych siłą poprzeczną powinien być spełniony warunek:
F=< FRj = fd (0,6 AnV + AnT nV/n); n - liczba śrub w połączeniu; nV - liczba śrub w ścinanej części przekroju netto; AnV , AnT - pole ścinanej i rozciąganej części przekroju netto.
4.Nośność połączeń spawanych pachwinowych i czołowych
Wymiary obliczeniowe i wymagania konstrukcyjne.
Spoiny czołowe:
- grubość obliczeniową „a” przyjmuje się równą grubości cieńszej z
łączonych części,
- długość obliczeniową „l” spoin czołowych przyjmuje się równą długości
spoiny bez kraterów,
- przy łączeniu blach o różnych grubościach, należy zapewnić ciągłą zmianę
przekroju, stosując pochylenie nie większe niż:
1 : 1 - przy obciążeniach statycznych,
1 : 4 - przy obciążeniach dynamicznych.
Nośność połączenia na spoiny czołowe:
- gdy pole przekroju obliczeniowego spoin jest niemniejsze niż pole przekroju łączonych elementów oraz = 1 odrębne sprawdzenie nośności połączenia jest zbędne,
- gdy nie są spełnione warunki jw. to nośność połączeń należy sprawdzać :
(26)
gdzie:
σ ,τ -naprężenia w przekroju obliczeniowym połączenia(sprężyste),
- współczynniki wytrzymałości spoiny wg tablicy 11.
Spoiny pachwinowe:
- grubość obliczeniowa „a” przyjmuje się równą wysokości trójkąta wpisanego w przekrój spoiny,
- do obliczeń należy przyjmować nominalną grubość spoiny „a” podawaną w całkowitych mm( wyjątek- spoiny o grubości 2,5 ;3,5 mm),
- zaleca się tak dobierać grubość spoiny, aby spełnione były warunki:
(27)
gdzie :
t1, t2 - grubość cieńszej i grubszej części w połączeniu,
- długość obliczeniową spoin przyjmuje się równą sumarycznej długości spoin ∑li, w przypadku spoin przerywanych można uwzględniać w obliczeniach tylko te odcinki spoin, które spełniają warunki:
(28)
Nośność połączeń na spoiny pachwinowe:
wytrzymałość dla spoin pachwinowych w złożonym stanie naprężenia : (29)
gdzie:
= 0,7 dla stali Re ≤255 MPa,
= 0,85 dla stali 255 < Re ≤355 MPa,
= 1 dla stali 355 < Re ≤460 MPa.
5.Nośność prętów ściskanych i rozciąganych.
Elementy rozciągane
1. Przy projektowaniu prętów osiowo rozciąganych można pomijać wpływ zginania wywołany ciężarem własnym, jeżeli rzut poziomy pręta nie przekracza 6m.
2. Nośność na rozciąganie:
gdzie: N-siła osiowa w pręcie, NRt-obl. nośność na rozciąganie
gdzie: A-pole przekroju pręta, fd-wytrzymałość obl stali
3. Elementy osłabione otworami na łączniki lub zamocowane mimośrodowo:
gdzie:
-sprowadzone pole przekroju
4. Pręty osiowo obciążone i osłabione otworami na łączniki
,
5. Element złożony z kilku ścianek
gdzie: An-pole netto mniejszego przekroju pojedynczej ścianki, Rm, Re -wytrzymałość na rozciąganie i granica plastyczności stali
6. Pręty pojedyncze zamocowane mimośrodowo (można pominąć wpływ mimośrod) warunek:
7. Połączenia prętów mimośrodowo zamocowanych na jeden łącznik:
,
gdzie:
-sprowadzone pole części przylgowej kształtownika
-pole netto części przylgowej kształtownika
8. Warunek nośności przy osłabieniu otworami:
gdzie: σ-naprężenie średnie dla przekroju brutto, Δσ-naprężenia od zginania dla przekroju brutto,
- wskaźnik osłabienia
9.Ograniczenie smukłości:
- dla prętów kratownic,
- dla cięgien bez wstępnego naciągu
Elementy ściskane osiowo
1.Przy projektowaniu prętów osiowo ściskanych można pomijać wpływ zginania wywołany ciężarem własnym, jeżeli iloczyn smukłości względnej w płaszczyźnie pionoweji rzutu poziomego pręta nie przekracza 6m.
2.Nośność obliczeniowa przy osiowym ściskaniu
, dla przekrojów klasy 1,2 i 3 przyjmuje się ��=1, dla przekroju klasy 4 ��=
p
3.Smukłość względna przy wyboczeniu
gdzie: Ncr- siła krytyczna przy wyboczeniu
4.Smukłośc względna przy wyboczeniu giętnym
Lub w przypadku klasy 4
gdzie: ��-smukłość pręta
gdzie: l0-długośc obliczeniowa pręta w osiach podpór, le - długośc wybooczeniowa, ��-współczynnik długości wyboczeniowej, ��p-smukłość porównawcza
5.Stateczność elementów ściskanych osiowo
gdzie:��-współczynnik wyboczeniowy
Elementy ściakne mimośrodowo
Nośność elementów ściskanych i zginanych
Gdzie:
6. Klasy przekrojów stalowych
Klasa przekroju - stopień odporności elementu na miejscową utratę stateczności. Klasa przekroju zależy od warunków podparcia, rozkładu naprężeń i smukłości ścianek.
Klasa 1. przekroje klasy 1 mogą osiągać nośność uogólnionego przegubu plastycznego, a w stanie pełnego uplastycznienia przy zginaniu mają zdolność do obrotu, niezbędną do plastycznej redystrybucji momentów zginających.
Klasa 2. przekroje klasy 2 mogą osiągnąć stan uogólnionego przegubu plastycznego, lecz w skutek miejscowej niestateczności plastycznej wykazują ograniczoną zdolność do obrotu, uniemożliwiającą redystrybucję momentów zginających.
Klasa 3. przekroje klasy 3 charakteryzują się tym, że ich nośność jest uwarunkowana początkiem uplastycznienia strefy ściskanej(σc max<=fd)
Klasa 4. przekroje klasy 4 tracą nośność przy największaą naprężeniach ściskających (lub średnich ścinających) mniejszych niż granica plastyczności.
Pole przekroju czynnego przy ścinaniu siłą Vi dla teowników, ceowników i dwuteowników: AV = ΣhWtw
7.Warunki nośności elementów zginanych dla różnych klas przekrojów.
Warunek nośności (stateczności)
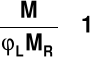
M -moment obliczeniowy
MR - nośność obliczeniowa na zginanie
![]()
- współczynnik zwichrzenia
- dla przekrojów klasy 1 , 2
![]()
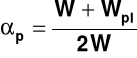
- obliczeniowy wskaźnik rezerwy
plastycznej przekroju
![]()
S1,S2 - momenty statyczne ściskanej i rozciąganej strefy przekroju wg osi obojętnej
-dla przekroju symetrycznego
![]()
S=S1=S2
W - minimalny wskaźnik wytrzymałości sprężystej
przekroju przy zginaniu (dla włókien ściskanych lub
rozciąganych)
- dla przekrojów klasy 3 , 4
![]()
![]()
=1 dla przekroju klasy 3
![]()
<1 dla przekroju klasy 4
Wc - wskaźnik wytrzymałości sprężystej dla strefy
Ściskanej
fd - wytrzymałość obliczeniowa stali
8.Stężenia hal stalowych
Stężenia dachowe
tężniki połaciowe poprzeczne: rola : przejęcie wiatru na ściany szczytowe oraz stężenia pasa górnego (ściskanego) dźwigara dachowego, pola skrajne, po obu stronach dylatacji, nie rzadziej niż co 8 pole i nie rzadziej niż 120m
tężniki połaciowe podłużne: połączenie tężników poprzecznych i otworzenie wraz z nimi sztywnej ramy w płaszczyźnie dachu, przejęcie parcia wiatru na ściany podłużne, usztywnienie konstrukcji dachu gdy rozstaw słupów głównych jest większy od rozstawu dźwigarów, przeniesienie obciążeń poziomych na część sztywną konstrukcji, gdy słupy główne są przegubowo podparte; pola przy okapie i linii słupów wewnętrznych rozdzielających nawy
tężniki pionowe: zabezpieczenie dźwigarów przed przesunięciem lub przewróceniem się zwłaszcza w trakcie montażu; w polach przyległych do tężników połaciowych poprzecznych(w przypadku hali z suwnicami- wzdłuż całej długości hali), przy okapach, pod ściankami świetlików i nie rzadziej niż co 15m .
tężniki poprzeczne i podłużne pasa dolnego(pomocnicze); dodatkowe usztywnienie hali w przypadku, gdy rozstaw słupów głównych jest większy od rozstawu dźwigarów, pomoc w przejęciu sił poziomych od wiatru, gdy pasy dolne są ściskane, pola przy ścianach bocznych i szczytowych
stężenia ścian:
tężniki górne ścian: przenosi siły poziome od parcia wiatru ścianki szczytowe, współdziała w przenoszeniu sił poziomych podłużnych wywołanych pracą suwnicy; pola skrajne, pola przy dylatacji, pola nas tężnikami dolnymi ścian
tężniki dolne ścian: przenosi siły poziome wywołane parciem wiatru na ściany szczytowe i siły poziome podłużne wywołane pracą suwnicy; pole środkowe lub pola skrajne lub co 1/3 długości hali (zbyt wiele tężników wpływa niekorzystnie, ograniczając ruchy termiczne)
tężniki hamowne: wzdłuż belek podsuwnicowych na pełnej długości belek; przenosi siły poziome poprzeczne i podłużne, wywołane pracą suwnicy
9. Obciążenia belek podsuwnicowych
- ciężar stały (własny belki podsuwnicowej)
- oddziaływanie suwne
- oddziaływanie pomostów
- obciążenia wiatrem (oddziaływanie wiatru na suwnicę, oraz oddziaływanie wiatru na ładunek
10. Projektowanie belek podsuwnicowych
1.1 Obciążenia pionowe
- max nacisk koła suwnicy od udźwigu
P.umax=Q*(L.s-E)/n*L.s
- max nacisk koła suwnicy od ciężaru własnego
P.gmax=P.max-P.umax
- min nacisk koła suwnicy
P.min=[(Q+G.s)/n]-P.max
- min nacisk koła suwnicy od udźwigu
P.umin=Q*E/n*L.s
-min nacisk koła suwnicy od ciężaru własnego
P.gmin=P.min-P.umin
Wartość obciążeń pionowych na szynę
- charakterystyczne
Vkmax=β*(P.umax+P.gmax)
Vkmin=β*(P.umin+P.gmin)
β-wsp.dynamiczny
β=1 dla obc. charakterytycznych
- obliczeniowe
V.max=β*(P.umax*ψ.fu+P.gmax*ψ.fg)
V.min=β*(P.umin*ψ.fu+P.gmin*ψ.fg)
β-T1 PN-86/B-02005
ψ.fu-wsp. obciążenia technologiczne
ψ.fg=1.1 - wsp. ciężar własny
1.2 Obciążenia poziome prostopadłe do toru jazdy
- charakterystyczne
H.kpmax=k*P.max
K.kpmin=k*P.min
k-współczynnik, pkt. 3.2 PN-86/B-02005
- obliczeniowe
H.pmax=k*(P.umax*ψ.fu+P.gmax*ψ.fg)
H.pmin=k*(P.umin*ψ.fu+P.gmin*ψ.fg)
1.3Obciążenia poziome równoległe do toru jazdy
- charakterystyczne
H.krmax=0.12*P.max
K.krmin=0.12*P.min
- obliczeniowe
H.rmax=0.12*(P.umax*ψ.fu+P.gmax*ψ.fg)
H.rmin=0.12*(P.umin*ψ.fu+P.gmin*ψ.fg)
Założenia:
L.s - rozpiętość suwnicy w osi szyn [m]
Q - udźwig suwnicy [kN]
G.s - masa suwnicy [kN]
n=2 - liczba kół suwnicy po jednej stronie
E - min. odległość haka od osi szyny [m]
11. Projektowanie dwugałęziowych słupów stalowych pod belkami podsuwnicowymi.
12. Obciążenia hal stalowych
Hale obciążone są min. :
- Obciążeniami wywołanymi przez parcie i ssanie wiatru
- Obciążeniami wywołanymi zaleganiem śniegu
- Obciążeniami wywołanymi działaniem ciężaru własnego
- Obciążeniami wywołanymi ciężarem suwnic obciążeń ich pracą
13. Warunki nośności słupów i rygli ram hal stalowych
14. Projektowanie połączeń słupów i rygli ram hal stalowych
15. Efekty II rzędu w projektowaniu hal stalowych
Teoria II rzędu stanowi o niedokładności pionowości ramy przesuwnej oraz nadmiernej jej podatności na obciążenia poziome.
Wg teorii II rzędu należy obliczać układy wielokondygnacyjne wrażliwe na efekty II rzędu (H≥0,1).
W przypadku układów jednokondygnacyjnych i układów o węzłach nieprzesuwnych można nie uwzględniać efektów II rzędu (H<0,1)..
Wskaźnik wrażliwości na efekty II rzędu:
1) ustalenie parametru niedoskonałości ramy w postaci kąta wstępnego przechyłu kondygnacji:
![]()
, gdzie: ![]()
lecz r1≤1;
` ![]()
;
h - wysokość kondygnacji w m,
n - liczba słupów danej kondygnacji w rozpatrywanej płaszczyźnie.
2) ustalenie wskaźnika:
![]()
ΣH - sumaryczne obciążenie poziome powyżej rozpatrywanej kondygnacji (siła poprzeczna od obciążenia zewn).
ΣN - sumaryczne obciążenie pionowe przenoszone przez słupy rozpatrywanej kondygnacji.
Ψ0 - wstępny przechył rozpatrywanej kondygnacji.
ΔΨ - przyrost przechyłu spowodowany działaniem sił poziomych (H+H0).
Siły wewn. II rzędu (zwiększone s stosunku do sił I rzędu wskutek przemieszczeń poziomych układu) można wyznaczać w sposób przybliżony, przyjmując do obliczeń wg teorii I rzędu zastępcze siły poziome HII:
![]()
αH - wskaźnik wrażliwości
![]()
, gdzie ΣP- oddziaływania pionowe rygli rozpatrywanej kondygnacji.
H - siła pozioma od obciążenia zewnętrznego na poziomie rozpatrywanej kondygnacji.
Wyszukiwarka
Podobne podstrony:
zelbet test, Skrypty, PK - materiały ze studiów, I stopień, SEMESTR 7, Konstrukcje Betonowe II, egza
KMTprojekt3, Skrypty, PK - materiały ze studiów, I stopień, SEMESTR 7, Konstrukcje stalowe II, pomoc
PROJEKTOWANIE BELKI270, Skrypty, PK - materiały ze studiów, I stopień, SEMESTR 7, Konstrukcje stalow
ZESTAWIENIE STALI -podciągpp, Skrypty, PK - materiały ze studiów, I stopień, SEMESTR 7, Konstrukcje
zest stali zb, Skrypty, PK - materiały ze studiów, I stopień, SEMESTR 7, Konstrukcje stalowe II, pom
zelbet test, Skrypty, PK - materiały ze studiów, I stopień, SEMESTR 7, Konstrukcje Betonowe II, egza
Projekt mostu sprężonego, Skrypty, PK - materiały ze studiów, I stopień, SEMESTR 8, Podstawy konstru
temat 3, Skrypty, PK - materiały ze studiów, I stopień, SEMESTR 2, Geodezja, od Donia - geodezja WIŚ
WYMAGANIA TECHNICZNE PODSYPKI, Skrypty, PK - materiały ze studiów, I stopień, SEMESTR 7, Podstawy bu
Pytania na geodezje, Skrypty, PK - materiały ze studiów, I stopień, SEMESTR 2, Geodezja, od Donia -
temat, Skrypty, PK - materiały ze studiów, I stopień, SEMESTR 2, Geodezja, od Donia - geodezja WIŚ,
koszukla 3, Skrypty, PK - materiały ze studiów, I stopień, SEMESTR 2, Geodezja, od Donia - geodezja
POLIGON SPRAWOZDANIE, Skrypty, PK - materiały ze studiów, I stopień, SEMESTR 2, Geodezja, od Donia -
bolkowska, Skrypty, PK - materiały ze studiów, I stopień, SEMESTR 8, EZP, EZP, BUDOWN i KRYZYS
STANDARDY KONSTRUKCYJNE NAWIERZCHN, Skrypty, PK - materiały ze studiów, I stopień, SEMESTR 7, Podsta
opis t, Skrypty, PK - materiały ze studiów, I stopień, SEMESTR 4, BOF
więcej podobnych podstron