1.Podaj def. Udładu odniesieni-jakie znasz układy. Układ odniesienia nazywamy układ współrzędnych związany z ciałem lub grupą ciał względem których opisywany jest ruch innego ciała. Kartezjański, cylindryczny, sferyczny, biegunowy. Punkt materialny (masa punktowa) - ciało fizyczne obdarzone masą, ale mające nieskończenie małe rozmiary (będące punktem).Punkt materialny nie jest obiektem istniejącym w rzeczywistości. Jego stosowanie jest przybliżeniem i upraszcza znacząco opis ruchu danego ciała.

2. Podaj def. Skalara, jakie znasz wielkości skalarne. Skalar wielkość fizyczna całkowicie określona przez podanie jedynie jej wielkości (wymiaru) (temperatura, długość, masa,..) Podaj def. Wektora- jakie znasz wielkości wektorowe w fiz. Wektor wielkość zorientowana w przestrzeni wymagająca dla jej określenia zarówno wartości (wymiaru) oraz kierunku i zwrotu (siła, przyspieszenie, prędkość..) Skalar - wielkość, do której określenia wystarczy jedna liczba rzeczywista np. długość, pole, objętość.

Wektor - obiekt geometryczny mający moduł (zwany też długością), kierunek i zwrot określający orientację wzdłuż danego kierunku

8. I zasada dynamiki: (zasada bezwładności)- przez bezwładność rozumiemy właściwości ciała decydujące o tym, że ciało bez działania sił nie może zmienić ani wartości, ani kierunku swojej prędkości. Czyli bez działania siły pozostaje w stanie w jakim był wcześniej. II zasada dynamiki: (przyczyna zmiany prędkości)
- suma wektorowa wszystkich sił działających na ciało. Zmienia jego prędkość czyli nadaje mu przyspieszenie. (
) szybkość zmiany pędu ciała jest równa sile wypadkowej działającej na to ciało. III zasada dynamiki: (wzajemne oddziaływanie dwóch ciał) gdy 2 ciała oddziaływają wzajemnie to siła wywierana przez to ciało drugie na ciało pierwsze jest równa i przeciwnie skierowana do siły z jaką ciało pierwsze działa na ciało drugie.

9. Podaj def. energii: Energią kinetyczna K Związana jest z ruchem ciała, ciało posiada energię kinetyczną ponieważ porusza się. Puntu materialnego o masie m poruszającego się z prędkością v, dużo mniejszą od prędkości światła c. Energia potencjalna energia wynikająca z położenia lub konfiguracji układu ciał względem siebie. Energia potencjalna= praca wykonana przez siły zewnętrzne przy przesunięcia ciała z Puntu odniesienia o zerowej energii potencjalnej do danego punktu o położeniu r.

10. Podaj def. sił: Siły zachowawcze grawitacyjne, sprężystości. Jeżeli praca wykonana przez siłę przemieszczającą cząstkę z punktu A do punktu B jest niezależna od toru łącząca punkty A i B, to siła jest siłą zachowawczą. Siły rozpraszające tarcie.

12. Podaj i omów prawo zachowania energii mechanicznej.

- Jeżeli wszystkie siły działające na cząstkę są zachowawcze, to całkowita energia cząstki w każdym jej położeniu jest wielkością stałą, zwaną całkowitą energią mechaniczną

- Energia układu izolowanego może przekształcać się z jednej postaci w inną, jednak energia całkowita w jej różnorodnych formach nie może być ani stworzona z niczego, ani też unicestwiona

Podaj prawo zachowania energii (energii mechanicznej) jeżeli wszystkie siły działające na cząstkę są zachowawcze to całkowita energia cząstki w każdym jej położeniu jest wielkością stałą, zwaną całkowitą energią mechaniczną. Siła niezachowawcza np. siła tarcia, ciepło, promieniowanie. Energia układu izolowanego może przekształcać się z jednej postaci w inną, jednak energia całkowita w jej różnorodnych formach nie może być ani stworzona z niczego, ani też unicestwiona.

13. Zasada zachowania energii całkowitej

To, że energia jest tak ważną wielkością wynika z jednego podstawowego faktu - obowiązuje zasada zachowania energii.

Gdyby powyższa zasada nie obowiązywała, a więc gdyby energia zmieniała się bez istotnego powodu, to nie byłoby sensu uczyć się, ani wzoru na energię kinetyczną, ani na potencjalną, ani na żadną inną, bo i tak nie wiadomo byłoby czy w danym momencie ta wielkość jeszcze ma poprzednio znaną wartość.

Zasada zachowania energii jest jedną z zasad podstawowych w fizyce. Oznacza to, że ma ona zastosowanie do wszystkich działów fizyki, a także że sprawdza się z bardzo daleko posuniętą dokładnością (pewne odstępstwa na bardzo krótką chwilę czasu mogą wystąpić zjawiskach fizyki kwantowej i wynikają z zasady nieoznaczoności Heisenberga, ale to już "wyższa szkoła jazdy").

Energia całkowita

Energia całkowita, to po prostu energia zawierająca wszystkie możliwe jej postacie: kinetyczną, potencjalną ciężkości, potencjalną sprężystości, elektryczną, magnetyczną, chemiczną, jądrową, świetlną (właściwie to też jest forma energii pola elektromagnetycznego) itd....

E_całkowita = E_mechaniczna + E_grawitacyjna + E_{elektromagnetyczna} + E_jądrowa + ...

14. Sformułowanie zasady zachowania pędu [edytuj]

Suma wektorowa wszystkich pędów izolowanego układu punktów materialnych pozostaje stała.

Układ izolowany, oznacza, że nie działają na niego siły zewnętrzne. Obecność sił wewnętrznych, między elementami układu, nie zmienia pędu układu.

Zasada nie dotyczy układów nie-izolowanych. Gdy na układ ciał działa siła zewnętrzna, wówczas pęd wypadkowy układu zmienia się. Zasada zachowania pędu wynika wprost z II zasady dynamiki w postaci uogólnionej. Można ją również wywieść z niezmienniczości lagranżjanu (hamiltonianu) względem przesunięć w przestrzeni (jeśli wszystkie punkty przesuniemy w przestrzeni o
to nowy układ będzie identyczny z pierwotnym). Sytuacji takiej odpowiada brak członu potencjalnego w lagranżjanie (hamiltonianie).

Przykłady zastosowania [edytuj]

• Zderzenia sprężyste i niesprężyste.

• Odrzut.

Odrzut

Przejawem działania tej zasady jest zjawisko odrzutu, polegające na tym, że przy rozpadzie ciała na dwie części obie otrzymują pędy jednakowe co do wartości bezwzględnej, lecz przeciwnie skierowane względem układu odniesienia, w którym ciało przed rozpadem pozostawało w spoczynku.

15. Podaj definicję momentu pędu.

Moment pędu to iloczyn wektorowy dwóch wektorów. Wektora położenia i wektora pędu. Oznacza to tyle, że wartość momentu pędu jest to iloczyn wartości wspomnianych wektorów. Wektor momentu pędu jest prostopadły do płaszczyzny, na której leżą wektor położenia i pędu (czyli prędkości).

L - moment pędu

r - promień wobec którego określamy moment

p - pęd punktu materialnego.

Podaj def. momentu pędu. moment pędu cząstki o pędzie p i znajdującej się w punkcie określonym wektorem wodzącym r wynosi.
wektor momentu pędu jest prostopadły do płaszczyzny wyznaczonej przez p i r . Pochodna momentu pędu bryły sztywnej względem czasu t jest równa momentowi siły działającej na tę bryłę

16. Podaj def. momentu bezwładności. Moment bezwładności bryły względem danej osi nazywamy sumę iloczynów mas poszczególnych punktów bryły i kwadratów ich odległości od danej osi.

. Moment bezwładności I bryły względem dowolnej osi jest równy sumie momentów bezwładności Is względem osi równoległej przechodzącej przez środek masy bryły oraz iloczynu masy m tej bryły i kwadratu odległości h obu osi. Twierdzenie to pokazuje nam jaki jest moment bezwładności względem osi przechodzącej przez środek masy tego ciała a momentem względem dowolnej innej osi równoległej do tamtej. Moment siły (moment obrotowy) — siły F względem punktu O jest to iloczyn wektorowy promienia wodzącego r, o początku w punkcie O i końcu w punkcie przyłożenia siły oraz siły F:

.

17. Podaj definicję energii kinetycznej w ruchu obrotowym.

Energia kinetyczna w ruchu obrotowym jest wprost proporcjonalna do kwadratu szybkości kątowej:

I - odpowiednim momentem bezwładności,

ω - prędkość kątowa.

Energia kinetyczna ruchu obrotowego E_r w ujęciu klasycznym dana jest wzorem: E_r=Iω²/2, gdzie I moment bezwładności ciała względem osi chwilowego obrotu, ω chwilowa prędkość kątowa obrotu ciała wokół tej samej osi.

18. Podaj zasady dynamiki Newtona dla ruchu obrotowego.

I zasada dynamiki:

Jeśli wypadkowy moment siły względem wybranej osi obrotu, jest równy zeru, to obiekt pozostaje w spoczynku lub jest w ruchu obrotowym ze stałą prędkością kątową wokół tej osi

II zasada dynamiki:

Jeżeli wypadkowy moment sił jest różny od zera, to obiekt jest w ruchu obrotowym z przyśpieszeniem kątowym wprost proporcjonalnym do wypadkowego momentu siły i odwrotnie proporcjonalnym do wypadkowego momentu bezwładności:

19. Jakie układy nazywamy inercjalnymi. Z pierwszej zasady dynamiki wynika, że jeśli na ciało nie działają żadne siły lub działają siły zrównoważone (F=0), to ciało jest nieruchome lub porusza się ruchem jednostajnie prostoliniowym. Ponieważ ruch jest zmienną położenia ciała względem układu odniesienia , możemy zapytać czy w każdym układnie odniesienia będzie spełniona I zasada dynamiki Newtona. Otóż okazuje się, że zasada ta obowiązuje tylko w inercjalnych układach odniesienia, w których I zasada dynamiki nie jest spełniona, noszą nazwę układów nieinercjalnych . Pierwsza zasada dynamiki jest w istocie postulatem, że układ inercjalny istnieje. Jeżeli ciało, na które nie działają żadne siły, pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym nazywamy inercjalnym układem odniesienia. Pierwsza zasada dynamiki Newtona nie jest prawem przyrody lecz postulatem układu inercjalnego w przyrodzie. Układ związany z Ziemią jest przybliżeniem układu inercjalnego.

20. Co wiesz o transformacjach Galileusza Punkt P nieruchomy w stacjonarnym układzie O1, obserwowany jest z układu O2 poruszającego się z prędkością v względem układu O1. V=(v,0,0)=const. X2=x1-vt, y2=y1, z2=z1, t2=t1. Transformacje Galileusza to układ równań wiążący współrzędne i czas dwóch układów inercjalnych (słuszny gdy v<c) . Niezmienność Galileusza. Czas we wszystkich układach inercjalnych jest taki sam, biegnie jednakowo t2=t1. Galileuszowskie dodawanie prędkości
v1=v2+v. Przyspieszenie jest niezmiennikiem transformacji Galileusza a2=a1. Zasada względności Galileusza istnieje nieskończenie wiele układów inercjalnych w których spełniona jest pierwsza i druga zasada dynamiki Newtona.

x` - współrzędna cząstki zmierzona przez obserwatora O`

x - współrzędna cząstki zmierzona przez obserwatora O

t - czas ruchu układu O` zmierzony przez obserwatora O

t` - czas ruchu układu O zmierzony przez obserwatora O`

21. Podaj Postulaty STW. Prędkość światła jest taka sama we wszystkich inercjalnych układach odniesienia. Zasada względności obowiązuje dla wszystkich praw fizyki - wszystkie prawa fizyki muszą być takie same we wszystkich układach inercjalnych poruszających się względem siebie ruchem jednostajnie prostoliniowym.

Albert Einstein oparł swe rozumowanie na dwóch postulatach:

• Zasadzie względności

Zasada głosząca, że prawa fizyki są jednakowe we wszystkich układach inercjalnych — musi obowiązywać dla wszystkich praw zarówno mechaniki jak i elektrodynamiki.

• Niezmienność prędkości światła

Prędkość światła w próżni jest taka sama dla wszystkich obserwatorów, taka sama we wszystkich kierunkach i nie zależy od prędkości źródła światła.

Światło nie potrzebuje jakiegokolwiek ośrodka (eteru) do rozchodzenia się.

25. Co wiesz o relatywistycznej masie.

Porównując wzór na pęd ze wzorem klasycznym:

możemy zauważyć podobieństwo. Różnica polega na zachowaniu się masy - według fizyki klasycznej masa ciała pozostawała stała, w SWT masa rośnie wraz z prędkością i można ją opisać wzorem (tzw. masa relatywistyczna):

We wzorach tych m₀ oznacza tzw. masę spoczynkową, czyli masę jaką ciało posiada gdy jest nieruchome.

26.. Relatywistyczna energia całkowita:
,
,
,
należy zauważyć że ta definicja energii całkowitej w mechanice relatywistycznej nie zawiera enerii potencjalnej. Równoważność masy i energii jest jedyną z najważniejszych konsekwencji szczególnej teorii względności.

Energia całkowita (E) - to całkowita energia, jaką ciało posiada (w związku ze swoją masą).

gdzie m oznacza masę relatywistyczną, a m₀ masę spoczynkową ciała.

27. Podaj definicje drgań, drgań harmonicznych.

Drgania - zjawisko fizyczne które charakteryzuje się powtarzalnością w czasie funkcji A(t). Przez co wielkości fizyczne na przemian rosną i maleją w czasie.

Drgania harmoniczne - powstają, gdy siła sprowadzająca układ drgający do położenia równowagi jest proporcjonalna do wychylenia układu z tego położenia.

Podaj def. drgań, drgań harmonicznych: Oscylacje (tzw. drgania) poruszający się obiekt pozostaje w pobliżu ustalonego miejsca - punktu równowagi. Przykłady takich drgań to: ciężarek na sprężynie, wahadło matematyczne, ruch elektronów w atomach, ruch fotonów między zwierciadłami lasera. Drgania harmoniczne to takie drgania, w których wielkość charakteryzująca dany układ zmienia się z czasem sinusoidalnie lub cosinusoidalnie. Ruchem drgającym lub wprost drganiami nazywamy dowolne zjawisko fizyczne (każdy ruch lub zmianę stanu) charakteryzujące się powtarzalnością w czasie wielkości A(t) opisującej ten proces.

28. Podaj definicję logarytmicznego dekrementu tłumienia.

Logarytmiczny dekrement tłumienia jest to logarytm naturalny stosunku dwóch amplitud w chwilach t i t+T. Oznaczając logarytmiczny dekrement tłumienia literą λ (lambda) możemy zapisać:

Podaj i omów wzór na logarytmiczny dekrement tłumień. Logarytmiczny dekrement tłumienia jest to logarytm naturalny stosunku dwóch amplitud w chwilach
i
. Oznaczając logarytmiczny dekrement tłumień literą
(lambda) możemy zapisać

29. Co wiesz o rezonansie. Drgania ciała może wywoływać zewnętrzna siła zmieniająca się okresowo, zwana siłą wymuszającą
. Drgania wymuszane mają częstotliwość v taką samą, jak okresowo zmienna siła, ale na ogół różną od częstotliwości własnej ciała. Jeżeli częstotliwość siły wymuszającej i częstotliwość drgań własnych są sobie równe, amplituda osiąga wartość maksymalną. Takie zjawisko nazywamy rezonansem, a częstotliwość wymuszającą drgania rezonansowe częstotliwością rezonansową. Rezonans jest stosowany w celu wzmocnienia drgań nie tylko mechanicznych, ale także akustycznych i elektrycznych.

30. Podaj definicję fali porzecznej, podłużnej. Fala podłużna to fala, której drgania odbywają się w kierunku równoległym do kierunku jej rozchodzenia się. Przykładem fali podłużnej jest fala dźwiękowa. Fala poprzeczna jest to fala, w której kierunek drgań cząstek ośrodka jest prostopadły do kierunku rozchodzenia się fali.

Fale elektromagnetyczne są falami poprzecznymi.

Fale mechaniczne poprzeczne nie mogą rozchodzić się w objętości ośrodków płynnych, gdyż te nie przenoszą sił ścinających, a mogą rozchodzić się tylko w ciałach stałych. Na tej podstawie stwierdzono, że jądro Ziemi jest płynne. Fale na granicy ośrodków (np. fale na wodzie) są z natury falami poprzecznymi.

Przeciwieństwem fal poprzecznych są fale podłużne. W ciałach stałych, w których mogą rozchodzić się oba rodzaje fal, fale poprzeczne rozchodzą się wolniej.

31. . Napisz i wyjaśnij równanie różniczkowe ruchu falowego:
Funkcja
opisująca zaburzenia wywołane przejściem fali spełnia pewne równanie, które nazywamy różniczkowym równaniem ruchu fali. Aby znaleźć postać tego równania, obliczamy drugie pochodne funkcji Ψ(x,t) względem t oraz względem x.
,

Mnożąc obustronnie równanie przez k², natomiast przez ω², możemy porównać lewe strony tych równań.
. Ponieważ
, więc
Jest to równanie różniczkowe ruchu fali płaskiej propagującej się wzdłuż osi x z prędkością fazową V

31. Podaj równanie różniczkowe fali płaskiej.

32. Co wiesz o falach stojących: Fala wytworzona w ciele o skończonych rozmiarach odbija się od granicy tego ciała: np. fala wytworzona na napiętej strunie odbija się od obu punktów unieruchomienia struny. Fala odbita porusza się w kierunku przeciwnym niż fala padająca i superpozycja tych dwóch fal (fali padającej i odbitej) daje w wyniku falę wypadkową, zwaną falą stojącą.
Fala stojąca jest szczególnym przypadkiem fali, takiej, z której energia drgań nie jest przenoszona, lecz trwale zmagazynowana w poszczególnych ośrodkach.

Fala stojąca - powstaje, gdy nałożą się na siebie dwie fale sinusoidalne o tych samych amplitudach i częstotliwościach, biegnące w przeciwnych kierunkach. Zjawisko fali stojącej zachodzi, gdy fala emitowana przez źródło odbija się od przeszkody bez strat energii i wraca po tej samej prostej, nakładając się na falę padającą.

gdzie

Punkty o maksymalnej amplitudzie drgań zwane są strzałkami.

Węzły to punkty gdzie fala stojąca ma amplitudę A = 0.

33. . Opisz krótko Efekt Doppler'a - zjawisko obserwowane dla fal, polegające na powstawaniu różnicy częstotliwości, a tym samym i długości fali, wysyłanej przez źródło fali oraz zarejestrowanej przez obserwatora, który porusza się względem źródła fali. Dla fal rozprzestrzeniających się w ośrodku, takich jak na przykład fale dźwiękowe, efekt zależy od prędkości obserwatora oraz źródła względem ośrodka, w którym te fale się rozchodzą. W przypadku fal propagujących się bez udziału ośrodka materialnego, jak na przykład światło w próżni (w ogólności fale elektromagnetyczne), znaczenie ma jedynie różnica prędkości źródła oraz obserwatora.

Zjawisko polegające na pozornej zmianie częstotliwości źródła dźwięku odbieranego przez obserwatora poruszającego się względem źródła z prędkością

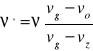
v_z - prędkość źródła, v_o -prędkość obserwatora, v_g -prędkość dźwięku w ośrodku,

34. Podaj wzór na równanie stanu gazu rzeczywistego.

Gdzie:

a - stała charakterystyczna dla danego gazu, uwzględniająca oddziaływanie między cząsteczkami gazu (cząsteczki gazu przyciągają się, w wyniku czego rzeczywiste ciśnienie gazu na ścianki naczynia jest mniejsze niż w przypadku, gdyby tego oddziaływania nie było),

b - stała charakterystyczna dla danego gazu, uwzględniająca skończone rozmiary cząsteczek, ma wymiar objętości, przez co uznawana jest za objętość mola cząsteczek gazu,

p - ciśnienie,

V_m =
- objętość molowa,

V - objętość

n - liczność (ilość gazu) w molach

T - Temperatura bezwzględna,

R - uniwersalna stała gazowa

35. Podaj def. entropia - entropia jest miarą nieuporządkowania układu cząstek. Im większy jest stan nieporządku położeń i prędkości w układzie tym większe prawdopodobieństwo, że układ będzie w tym stanie. Definicja termodynamiczna - entropia S jest termodynamiczną funkcją zależną tylko początkowego i końcowego stanu układu, a nie od drogi przejścia pomiędzy tymi stanami.

Entropia jest miarą nieuporządkowania układu cząstek. Im większy jest stan nieporządku położeń i prędkości w układzie tym większe prawdopodobieństwo, że układ będzie w tym stanie. Zgodnie z II zasadą termodynamiki, jeśli układ przechodzi z jednego stanu równowagi do drugiego, bez udziału czynników zewnętrznych, to jego entropia zawsze rośnie.

36. Czym zajmuje się statyka płynów.

Statyka płynów zajmuje się zagadnieniami równowagi i stateczności płynów, nieruchomych względem przyjętego układu odniesienia, a także siłami wywieranymi przez płyny na ścianki zbiorników bądź też na ścianki ciał zanurzonych w płynie i pozostających w spoczynku względem niego.

Statyka płynów to dział mechaniki płynów zajmujący się płynami nie poruszającymi się. Podstawową zależnością opisującą statyczny płyn jest:

gdzie p - ciśnienie, ρ - gęstość płynu, b - siły masowe (np. grawitacja)

Statyka płynów jest stosowana głównie w odniesieniu do cieczy (hydrostatyka).

W najczęściej spotykanym przypadku stałej gęstości płynu i jednorodnego pola sił masowych pochodzących od grawitacji: b_j = [0;0; − g] (gdzie: g - przyspieszenie ziemskie), wzór przybiera uproszczoną formę całkową:

p = p₀ − gρz

gdzie: z - wysokość, p₀ - ciśnienie na wysokości z = 0

Wzór ten jest współczesną postacią prawa Archimedesa, mówiącego że w płynie działa siła wyporu skierowana do góry równa ciężarowi wypartej cieczy.

W przybliżeniu braku grawitacji (pola sił masowych) otrzymujemy prawo Pascala, mówiące że ciśnienie w płynie jest wszędzie jednakowe.

37. Podaj równanie równowagi Eulera.

gdzie:

V - prędkość przepływu

p - ciśnienie

ρ - gęstość

F - tzw. jednostkowa siła masowa

Prawo Eulera [edytuj]

Sformułowane przez Eulera w 1755 roku mówi, że ^[1]:

Na płaskie ciało zanurzone w cieczy działa ciśnienie, którego wartość jest niezależna od orientacji tego ciała w przestrzeni.

W celu otrzymania matematycznej zależności opisującej to prawo rozpatrzmy różniczkową objętość płynu o podstawie trójkątnej i wysokości b (rys.4.). Płyn znajduje się w stanie równowagi (spoczynku). W stanie równowagi suma sił w poszczególnych kierunkach musi być równa zero:

Ponieważ:

Po podstawieniu otrzymujemy ostatecznie:

38. Podaj prawo Pascala.

Jeżeli na płyn nie działają siły masowe (mogą działać siły powierzchniowe), czyli wtedy gdy płyn pozostaje w spoczynku, to ciśnienie hydrostatyczne (statyczne) jest stałe w całej masie płynu.

Prawo Pascala mówi, że jeżeli na ciecz lub gaz w zbiorniku zamkniętym wywierane jest ciśnienie zewnętrzne, to ciśnienie wewnątrz zbiornika jest wszędzie jednakowe i równe ciśnieniu zewnętrznemu.

Prawo to jest spełnione dla cieczy, na którą działają jedynie siły powierzchniowe. Oznacza to, że dotyczy cieczy, które nie znajdują się w polu sił grawitacyjnych ^[1]. W warunkach rzeczywistych (gdy na ciecz działają dodatkowo siły grawitacji) cząsteczki z niższych warstw cieczy muszą "udźwignąć" cząsteczki znajdujące się nad nimi. Powoduje to różnice ciśnień między górną a dolną warstwą cieczy. Prawo często stosuje się w inżynierii (np. przy konstrukcji pras hydraulicznych, akumulatorów ciśnienia oraz tam).

39. Na czym polega paradoks hydrostatyczny (twierdzenie Stewina).

Paradoks hydrostatyczny - paradoks związany z mechaniką płynów, polegający na tym, że ciśnienie na dnie naczynia nie zależy wprost od ciężaru cieczy zawartej w naczyniu a zależy od wysokości słupa cieczy nad dnem. Natomiast parcie cieczy na dno naczynia zależy od pola powierzchni dna, wysokości słupa cieczy i ciężaru właściwego cieczy. Wynika z tego, że parcie cieczy na dno w naczyniach o różnych kształtach będzie takie samo, jeżeli pole powierzchni dna każdego z tych naczyń i wysokość słupa cieczy w tych naczyniach będą równe.

Paradoks hydrostatyczny - paradoks związany z mechaniką płynów, polegający na tym, że ciśnienie na dnie naczynia nie zależy wprost od ciężaru cieczy zawartej w naczyniu a zależy od wysokości słupa cieczy nad dnem. Natomiast parcie cieczy na dno naczynia zależy od pola powierzchni dna, wysokości słupa cieczy i ciężaru właściwego cieczy. Wynika z tego, że parcie cieczy na dno w naczyniach o różnych kształtach będzie takie samo, jeżeli pole powierzchni dna każdego z tych naczyń i wysokość słupa cieczy w tych naczyniach będą równe.

Fakt ten, stwierdzony po raz pierwszy przez holenderskiego uczonego Simona Stevina w XVI w., wydawał się wówczas paradoksalny, dlatego i dziś często nazywany jest paradoksem. Nazywany bywa także paradoksem Pascala, ponieważ Blaise Pascal w roku 1648 spopularyzował go demonstrując publicznie rozsadzenie beczki przy pomocy niewielkiej ilości wody (zobacz ilustrację). Doświadczenie to ilustrowało równocześnie prawo odkryte przez Pascala i nazwane jego imieniem.

---