FD II ; GRUPA L6 RZESZÓW, 2003-01-12
LAB_5B
Skład:
1. Robert Siwak
2. Tomasz Stasik
3. Rafał Bielecki
SPRAWOZDANIE
Sygnały i Systemy
TEMAT: Cyfrowa transmisja pasmowa sygnałów
1. Tematy zadań.
1.1 Program demonstracyjny lab_5_1d.m
Po otworzeniu powyższego pliku lab_5_1d.m należało przeanalizować działanie programu, a następnie wydrukować otrzymane przebiegi.
Następnym etapem było wyznaczenie odpowiedzi i badanie charakterystyk układu cyfrowego opisanego w dziedzinie Z. Należało zmodyfikować wartości parametrów w pliku poprzez wprowadzenie następujących wartości licznika L i mianownika M transmitancji układu:
L = [1 0]; M = [1 -0,8 0,2].
Po przeanalizowaniu programu należało wydrukować otrzymane charakterystyki.
W sprawozdaniu:
* Narysować schemat blokowy dla równania rekurencyjnego:
y[n]= u[n-1] + 0.8y[n-1] - 0.2y[n-2], opisującego układ cyfrowy, którego działanie analizowane jest przy pomocy programu lab_5_1.m.
* Stosując przekształcenie Z, dla parametrów licznika L=[0 1] i mianownika
M= [ 1 -0.8 0.2 ] transmitancji układu wyznaczyć y[n] wiedząc że x[n]= 1[n] oraz
y[-1]=0 i y[-2]=0.
* Wyznaczyć równanie rekurencyjne, a następnie na jego podstawie narysować schemat blokowy układu cyfrowego analizowanego przy pomocy programu lab_5_1.m, którego współczynniki licznika L= [1 0] i mianownika M= [1 -0.8 0.2].
* Stosując przekształcenie Z dla parametrów licznika L= [1 0] i mianownika
M= [1 -0.8 0.2] transmitancji układu, wyznaczyć y[n], wiedząc że x[n]= 1[n] oraz
y[-1]=0 i y[-2]=0.
* Opisać zaobserwowane różnice w odpowiedziach układów analizowanych przy pomocy programów lab_5_1d.m oraz lab_5_1.m ( wykorzystać uzyskane przebiegi oraz wyznaczone równania i schematy blokowe ).
1.2 Analiza programu lab_5_2.m
Do układu, którego schemat blokowy przedstawiono poniżej wyznaczyć transmitancję H(z) tego układu, a następnie charakterystyki: amplitudową i fazową .Wyznacz odpowiedź układu na deltę Kroneckera i dyskretny skok jednostkowy. Układ znajduje się w stanie zerowym.
Należało dokonać edycji pliku lab_5_2.m wprowadzając różne wartości dla licznika L i mianownika M transmitancji układu.
* L = [5 4], M = [1,5 -1].
* L = [5 4], M = [1,5 -0,75].
* L = [5 0], M = [1,5 -1].
* L = [0 4], M = [1,5 -1].
Po przeanalizowaniu programu lab_5_2.m należało wydrukować otrzymane charakterystyki.
W sprawozdaniu:
* Wyznaczyć równania rekurencyjne, a następnie na ich podstawie narysować schematy blokowe układu cyfrowego realizowanego przy pomocy programu lab_5_2.m dla wszystkich współczynników licznika L i mianownika M podanych powyżej.
* Stosując przekształcenia Z dla parametrów licznika L= [5 4] i mianownika M= [1,5 -1] transmitancji układu wyznaczyć y[n] wiedząc, że x[n]= δ[n] oraz y[-1]=0.
* Opisać zaobserwowane różnice w odpowiedziach układów analizowanych przy pomocy programu lab_5_2.m (wykorzystać przebiegi, równania i schematy blokowe).
1.3 Symulator cyfrowy analogowego szeregowego układu RL - program lab_5_3.m.
Dla układu którego schemat blokowy przedstawiono poniżej wyznaczyć transmitancje H(z) tego układu. Dokonać analizy wpływu okresu próbkowania T na dokładność otrzymanej z symulatora odpowiedzi impulsowej, dla trzech przypadków:
T=(1/2) τ ; T= (1/5) τ ; T= (1/10) τ gdzie τ = ( L/R ) jest stałą czasową układu. Pozostałe dane : R = 100 Ω L= 1mH. Podczas analizy należy zachować stały czas obserwacji : tobs= n*T = 5e-5.
Należało dokonać edycji pliku lab_5_3.m następnie wprowadzić obliczoną wartość T = kolejno 1/2, 1/5, 1/10 pamiętając o zmianie wartości n - liczby próbek, tak aby czas obserwacji tobs = 5e-5.
W sprawozdaniu:
* Narysować schemat analogowy oraz schemat cyfrowy układu.
* Wyznaczyć równie rekurencyjne dla schematu cyfrowego oraz równanie różniczkowe dla układu analogowego.
* Wyznaczyć transmitancję cyfrową H(z) układu.
* Opisać wpływ parametrów R,L,T na uzyskane przebiegi.
2. Analiza komputerowa.
Wszystkie wykorzystane podczas wykonywania laboratorium pliki były edytowane i analizowane za pomocą programu Matlab. Matlab zawiera wiele różnego rodzaju funkcji, które okazują się bardzo przydatne przy analizowaniu bieżącego tematu.
2.1 Analiza komputerowa pliku lab_5_1.m.
Po przeanalizowaniu pliku demonstracyjnego należało wydrukować wszystkie otrzymane charakterystyki.
Są to:
* odpowiedź impulsowa układu cyfrowego;
* odpowiedź skokowa układu cyfrowego;
* wymuszenie dla układu cyfrowego;
* odpowiedź układu cyfrowego;
* wykres Bodego dla charakterystyki amplitudowej układu;
* wykres Bodego dla charakterystyki fazowej układu.
Powyższe charakterystyki dołączone są do niniejszego sprawozdania.
Dalsza analiza pliku lab_5_1.m polegała na zmianie wartości licznika L i mianownika M transmitancji układu.
Nowe wartości to: L = [1 0]; M = [1 -0,8 0,2].
Następnie należało podobnie jak w powyższym przykładzie wydrukować 6 otrzymanych wykresów (identyczne zależności), które również dołączone są do sprawozdania.
2.2 Analiza komputerowa pliku lab_5_2.m.
Celem analizy pliku lab_5_2.m było wyznaczenie transmitancji H(z) danego układu,
a następnie charakterystyki amplitudowej i fazowej.
Aby w pełni zrealizować cel ćwiczenia należało analizować powyższy plik przy czterech różnych wartościach licznika L i mianownika M transmitancji układu:
* L = [5 4], M = [1,5 -1].
* L = [5 4], M = [1,5 -0,75].
* L = [5 0], M = [1,5 -1].
* L = [0 4], M = [1,5 -1].
Po przeanalizowaniu programu lab_5_2.m należało wydrukować otrzymane charakterystyki.
Są to:
* odpowiedź impulsowa układu cyfrowego;
* odpowiedź jednostkowa układu cyfrowego;
* wymuszenie dla układu cyfrowego;
* odpowiedź układu cyfrowego;
* wykres Bodego dla charakterystyki amplitudowej układu;
* wykres Bodego dla charakterystyki fazowej układu.
Aby porównać otrzymane charakterystyki przy zmiennych wartościach licznika i mianownika należało wydrukować charakterystyki tylko dla dwóch przypadków, a potem nanieść odpowiednie charakterystyki widoczne na monitorze na wydrukowane. W naszym przypadku zostały naniesione charakterystyki drugiej serii na pierwszą i czwartej na trzecią.
Wszystkie charakterystyki (wydrukowane i naniesione) są doczone do sprawozdania.
2.3 Analiza komputerowa pliku lab_5_3.m.
Dla podanego pliku lab_5_3.m należało wyznaczyć transmitancję H(z) (podany układ).
Ponadto należało zbadać wpływ okresu próbkowania T na dokładność otrzymanej z symulatora odpowiedzi impulsowej, dla trzech przypadków: T = ½ τ, T = 1/5τ, T = 1/10τ, gdzie ![]()
jest stałą czasową układu. Dla poprawności wyniku należało zachować stały czas obserwacji:
tobs = n*T = 5e-5, co można uzyskać poprzez zmianę ilości próbek n.
Aby otrzymać wykresy obrazujące wpływ okresu próbkowania na dokładność odpowiedzi impulsowej należało trzykrotnie zmodyfikować plik lab_5_3.m poprzez wprowadzenie obliczonej wartości okresu
T = 1/2τ i liczby próbek n.
Otrzymane charakterystyki należało wydrukować.
Analizując otrzymane wykresy można zauważyć, że są one praktycznie identyczne. Świadczy to najprawdopodobniej o popełnieniu błędu podczas obliczania T i n lub o niepoprawnym wprowadzeniu danych do programu.
Przy poprawnym obliczeniu, T i n mają odpowiednio wartość:
*
*
*
3. Rozwiązania analityczne zadań.
3.1 Analiza zadania z punktu b (plik lab_5_1.m).
* narysować schemat blokowy dla równania rekurencyjnego: y[n]= u[n-1] + 0.8y[n-1] - 0.2y[n-2].
y[n]= u[n-1] + 0.8y[n-1] - 0.2y[n-2].
* Stosując przekształcenie Z, dla parametrów licznika L=[0 1] i mianownika M= [1 -0.8 0.2] transmitancji układu wyznaczyć y[n] wiedząc, że x[n]= 1[n] oraz y[-1]=0 i y[-2]=0.
L=[0 1] M= [1 -0.8 0.2]
x[n-1] = y[n] - 0.8y[n-1] + 0.2y[n-2]
y[n] = x[n-1] + 0.8y[n-1] - 0.2y[n-2]
Po zastosowaniu przekształcenia Z otrzymamy:
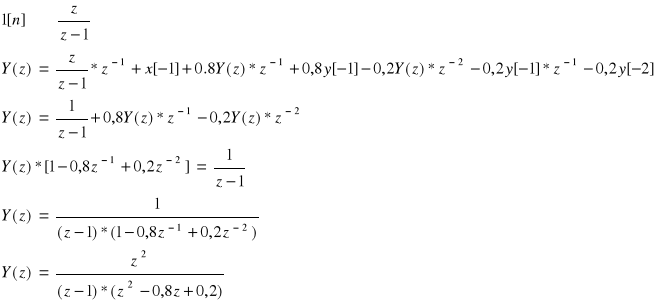
![]()
Obliczam pierwiastki równania: z2 - 0,8z +0,2=0
Δ=-0,16
![]()
lub ![]()
Stąd:
z1= 0,4-j0,2 ∨ z2= 0,4+j0,2
Podstawiając do powyższych obliczeń otrzymujemy:

Po podstawieniu obliczonych wartości A, B i C otrzymamy:
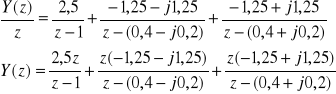
Korzystając z zależności ![]()
otrzymamy:
![]()
Inna postać rozwiązania wygląda następująco:
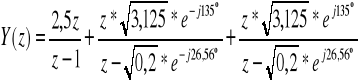
Stąd:
![]()
* . Wyznaczyć równanie rekurencyjne, a następnie na jego podstawie narysować schemat blokowy układu cyfrowego analizowanego przy pomocy programu lab_5_1.m, którego współczynniki licznika L= [1 0] i mianownika M= [1 -0.8 0.2].
L= [1 0] M= [1 -0.8 0.2]
x[n] = y[n] - 0,8y[n-1] + 0,2y[n-2]
y[n] = x[n] + 0,8y[n-1] - 0,2y[n-2]
Schemat blokowy ilustrujący powyższe równanie rekurencyjne ma postać:
* . Stosując przekształcenie Z dla parametrów licznika L= [1 0] i mianownika M= [1 -0.8 0.2] transmitancji układu, wyznaczyć y[n], wiedząc że x[n]= 1[n] oraz y[-1]=0 i y[-2]=0.
L= [1 0] M= [1 -0.8 0.2] oraz x[n]= 1[n] & y[-1]=0 & y[-2]=0
x[n] = y[n] - 0,8y[n-1] + 0,2y[n-2]
y[n] = x[n] + 0,8y[n-1] - 0,2y[n-2]
Po zastosowaniu przekształcenia Z otrzymamy:
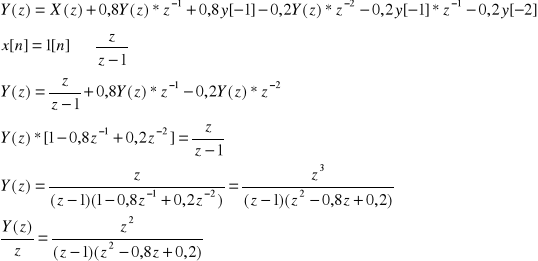
Obliczam pierwiastki równania: z2 - 0,8z +0,2=0
Δ=-0,16
![]()
lub ![]()
Stąd:
z1= 0,4-j0,2 ∨ z2= 0,4+j0,2
Podstawiając do powyższych obliczeń otrzymujemy:
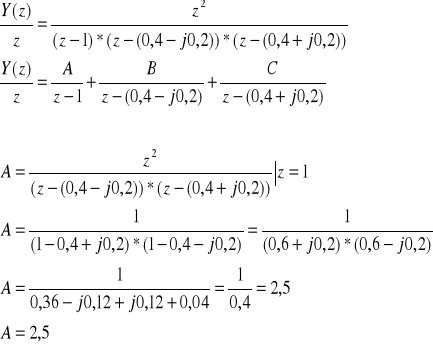

Po podstawieniu obliczonych wartości A, B i C otrzymamy:
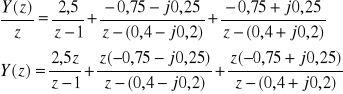
Korzystając z zależności ![]()
otrzymamy:
![]()
Inna postać rozwiązania wygląda następująco:
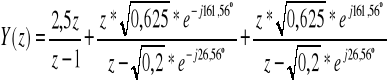
Stąd:
![]()
3.2 Analiza zadania z punktu c (plik lab_5_2.m).
* Wyznaczyć równania rekurencyjne, a następnie na ich podstawie narysować schematy blokowe układu cyfrowego realizowanego przy pomocy programu lab_5_2.m dla wszystkich współczynników licznika L i mianownika M.
* L = [5 4] M = [1,5 -1]
5x[n] + 4x[n-1] = 1,5y[n] - y[n-1]
1,5y[n] = 5x[n] + 4x[n-1] + y[n-1]
![]()
Schemat blokowy dla powyższego równania jest następujący:
Alternatywna postać schematu blokowego wygląda następująco:
* L = [5 4] M = [1,5 -0,75]
5x[n] + 4x[n-1] = 1,5y[n] - 0,75y[n-1]
1,5y[n] = 5x[n] + 4x[n-1] + 0,75y[n-1]
![]()
Schemat blokowy dla powyższego równania jest następujący:
* L = [5 0] M = [1,5 -1]
5x[n] = 1,5y[n] - y[n-1]
1,5y[n] = 5x[n] + y[n-1]
![]()
Schemat blokowy dla powyższego równania jest następujący:
* L = [0 4] M = [1,5 -1]
4x[n-1] = 1,5y[n] - y[n-1]
1,5y[n] = 4x[n-1] + y[n-1]
![]()
Schemat blokowy dla powyższego równania jest następujący:
* Stosując przekształcenia Z dla parametrów licznika L= [5 4] i mianownika M= [1,5 -1] transmitancji układu wyznaczyć y[n] wiedząc że x[n]= δ[n] oraz y[n-1]=0.
L= [5 4] M= [1,5 -1] x[n]= δ[n] oraz y[n-1]=0
![]()
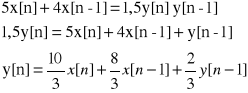
Po zastosowaniu przekształcenia Z otrzymamy:
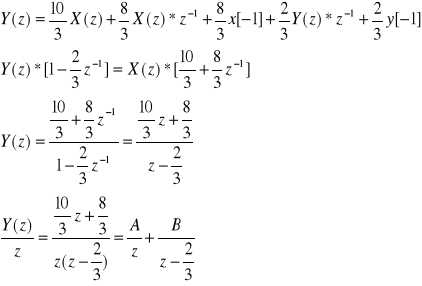
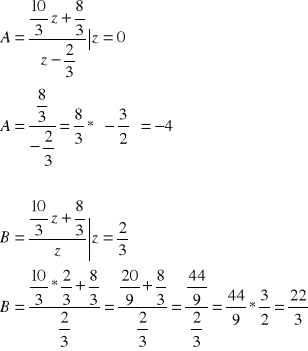
Po podstawieniu obliczonych wartości A i B otrzymamy:
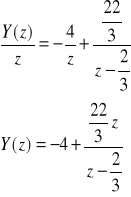
Stąd:
![]()
3.3 Analiza zadania z punktu d (plik lab_5_3.m).
* Narysować schemat analogowy oraz schemat cyfrowy układu.
* schemat cyfrowy układu:
* schemat analogowy układu:
* Wyznaczyć równanie rekurencyjne dla schematu cyfrowego oraz równanie różniczkowe dla układu analogowego.
* równanie rekurencyjne dla układu cyfrowego:
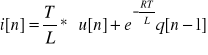
* równanie różniczkowe dla układu analogowego:
Powyższy układ opisany jest za pomocą równania:
![]()
(1)
Napięcie na cewce L wynosi:
![]()
Napięcie na rezystorze R wynosi:
![]()
Podstawiając do równania (1) otrzymany:
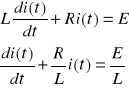
Jest to równanie na prąd w obwodzie.
Rozwiązanie równania składa się z dwóch członów:
* składowej wymuszonej iw(t), będącej całką szczególną równania różniczkowego niejednorodnego;
* składowej swobodnej is(t), będącej całką ogólną równania różniczkowego jednorodnego.
Odpowiedź układu w stanie nieustalonym jest sumą algebraiczną obu składowych:
i(t) = iw(t) + is(t)
Równaniem jednorodnym dla równania ![]()
jest równanie:
![]()
Rozwiązując powyższe równanie otrzymamy:
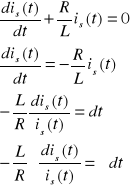
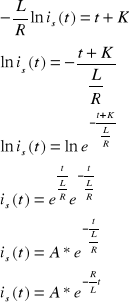
Rozwiązaniem szczególnym równanie niejednorodnego jest rozwiązanie dla stanu ustalonego, czyli:
![]()
Aby wyznaczyć stałą całkowania A należy skorzystać z warunku początkowego, w którym dla chwili
t = 0 prąd również wynosi zero.
Stąd otrzymamy:
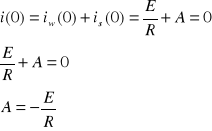
Prąd w obwodzie wynosi:
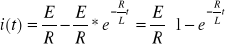
Stosunek ![]()
nazywa się stałą czasową.
Podstawiając τ do wzoru na prąd otrzymamy:
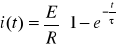
Pozostałe wartości oblicza się ze wzorów:
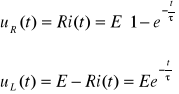
* Wyznaczyć transmitancję cyfrową H(z) układu.
Prąd i(t) spełnia równanie różniczkowe
Gdy rozpatrujemy powyższe równanie w dziedzinie operatorowej, to otrzymamy:
Gdy
e(t) = δ(t)
To i(t)=h(t)H(s)
Zatem:
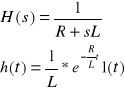
H(s) - transmitancja operatorowa
Transmitancja cyfrowa H(z)
![]()
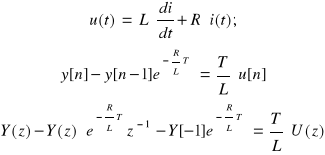
![]()
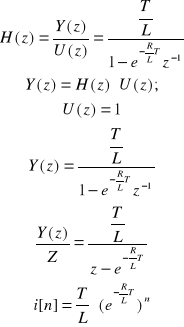
Opisać wpływ parametrów R,L,T na uzyskane przebiegi.
Stała czasowa ![]()
charakteryzuje obwód RL. Zależy ona wyłącznie od indukcyjności L i od rezystancji R. Z przesłanek teoretycznych można dojść do wniosku, że stała czasowa jest to taki czas, po upływie, którego składowa swobodna maleje co do wartości bezwzględnej e razy.
Jeżeli R = const, a indukcyjności L nadajemy kilka kolejnych różnych wartości, na przykład zmieniając wymiary geometryczne i liczbę zwojów cewki, to dużej wartości indukcyjności odpowiada duża stała czasu i powoli wzrastająca krzywa prądu, a małej wartości indukcyjności - mała stała czasu i szybko wzrastająca krzywa prądu. W teoretycznym przypadku granicznym L=0 (obwód o indukcyjności zerowej, czyli czysto rezystancyjny) stała czasu τ=0 i prąd w chwili początkowej t=0 wzrasta skokiem od wartości ustalonej początkowej i(0-)=0 do wartości ustalonej końcowej i(0-)=U/R. W tym przypadku teoretycznym nie ma w ogóle stanu nieustalonego, co jest opisaną już wcześniej cechą obwodów rezystancyjnych.
4. Wnioski.
Podczas laboratorium badaliśmy związki pomiędzy dyskretnymi sygnałami wymuszeń (sygnałami wejściowymi - x[n]) i dyskretnymi sygnałami odpowiedzi (sygnałami wyjściowymi y[n]).
Sygnały przedstawione są w postaci równań rekurencyjnych. Do badania takich sygnałów dyskretnych bardzo użyteczne jest przekształcenie Z. Dla sygnału dyskretnego w postaci ciągu f[n] transformatą Z nazywa się funkcję F(z) zmiennej zespolonej w postaci sumy nieskończonej:
![]()
dla tych z, dla których suma jest zbieżna.
Z powyższego wzoru można wyznaczyć transformaty Z dla różnych sygnałów.
Transformata Z skoku jednostkowego równa jest: ![]()
Transformata Z delty Kroneckera równa jest:
![]()
Stosując przekształcenie Z można obliczyć transformaty dla innych sygnałów.
Iloraz ![]()
nazywa się transmitancją układu cyfrowego.
Transmitancję można zdefiniować jako funkcję zmiennej zespolonej z przekształcającą transformatę Z wymuszenia w transformatę Z odpowiedzi.
PRz Sygnały i Systemy-Laboratorium.
6
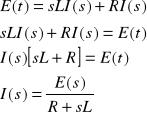
![]()
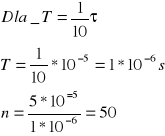
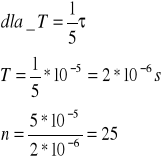
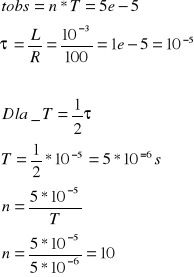
Wyszukiwarka
Podobne podstrony:
Transformata Laplace, Studia, Semestr 1, Sygnały i Systemy, Sprawozdanie 4
Transformata Laplace nasze 2, Studia, Semestr 1, Sygnały i Systemy, Sprawozdanie 4
Sygnaly i systemy 2FD Linia dluga, Studia, Semestr 1, Sygnały i Systemy, Sprawozdania
SiS Lab02 Micha 322 Kucab EF-DI1 2008 L06, Studia, Semestr 1, Sygnały i Systemy, Sprawozdanie 2
Sprawozdanie nr.3 - SiS, Studia, Semestr 1, Sygnały i Systemy, Sprawozdanie 3
LABSMO~2, Studia, Semestr 1, Sygnały i Systemy, Sprawozdania
TRAF, Studia, Semestr 1, Sygnały i Systemy, Sprawozdania
SiS LAB05 Dawid Warchoł EF-DI1 2009 L14, Studia, Semestr 1, Sygnały i Systemy, Sprawozdanie 5
LINIA, Studia, Semestr 1, Sygnały i Systemy, Sprawozdania
SiS LAB04 Dawid Warchoł EF-DI1 2008 L14, Studia, Semestr 1, Sygnały i Systemy, Sprawozdanie 4
sprawozdanie1 sis, Studia, Semestr 1, Sygnały i Systemy, Sprawozdanie 1
PARTI1, Studia, Semestr 1, Sygnały i Systemy, Sprawozdania
wiczenie 4, Studia, Semestr 1, Sygnały i Systemy, Sprawozdanie 3
ZET, Studia, Semestr 1, Sygnały i Systemy, Sprawozdania
SiS LAB03 Dawid Warchoł EF-DI1 2008 L14, Studia, Semestr 1, Sygnały i Systemy, Sprawozdanie 3
sprawozdanie3, Studia, Semestr 1, Sygnały i Systemy, Sprawozdanie 3
Sygn&Sys sem3 C2-Rownanie stanu, Studia, Semestr 1, Sygnały i Systemy, Sprawozdania
Sprawozdanie 2, Studia, Semestr 1, Sygnały i Systemy, Sprawozdanie 2
Filtracja i modulacja-spr, Studia, Semestr 1, Sygnały i Systemy, Sprawozdania
więcej podobnych podstron