Materiały dla studentów - ćwiczenia z logiki

Materiały 1

1. Kubuś Puchatek i Prosiaczek założyli pułapkę na słonie.

2. Malarze holenderscy malowali szybko bardzo duże obrazy.

3. Harry Potter wygrał Turniej Trójmagiczny i miał wiele kłopotów z popularnością.

4. Jeśli dzielny żołnierz znajdzie krzesiwo to spełnią się wszystkie jego marzenia.

5. Nazajutrz Kubuś Puchatek zjadł małe Conieco i odwiedził bardzo zmartwionego Kłapouchego.

6. Nieprawda, że spory filozoficzne powstają zawsze i tylko wtedy, gdy nauka przeżywa kryzys lub rozwija się zbyt gwałtownie.

Problemy1. Opisz kategorie składniowe (podając przykłady) a) najlepszy, b) spaceruje c) nieprawda, że

2. Skonstruuj schemat struktury składniowej zdania: a) Robinson wybudował prymitywną chatkę na wyspie

b) Neron podpalił Rzym ponieważ szukał natchnienia

c) Rozsądni ludzie milczą, gdy krzykliwi głupcy wyważają otwarte drzwi

d) Jeśli znamy podstawowe zasady gramatyki, to nie robimy rażących błędów stylistycznych.

e) Teleskop łatwo odsłania bardzo rozległe obszary nieba i zamyśleni patrzymy w nieskończony kosmos .

f) Ptolemeusz nie potrafił odkryć systemu heliocentrycznego, ponieważ nie posiadał odpowiednich przyrządów astronomicznych.

g) Nie jest prawdą, że jeżeli teoria Einsteina jest bardziej uniwersalna to teoria Newtona jest bez wartości.

h) Jeżeli czytasz swobodnie w obcym języku, to o ile nie potrafisz w nim mówić, to znasz go biernie.

i) Zaakceptujesz zajęcia z logiki i uznasz, że jest ona łatwo przyswajalna, jeśli nie masz złych wspomnień z lekcji matematyki w szkole średniej

3. Zrekonstruuj zdanie na podstawie danej struktury zdaniowej.

a) przejść na {Alicja ; druga [ strona (lustro) ] }

b) natychmiast po {przyjść do (Miś Puchatek; Sowa Przemądrzała); usiąść na [Miś Puchatek; małe (krzesełko)]}

4. Ustal kategorię następujących wyrażeń [w przypadku funktorów ustal ilość argumentów, rodzaj argumentów, wynik działania]. a) zły , b) chodzi , c) swój namiot Achillesa, d) biały jak śnieg, e) nie jest prawdą, że, f) chociażby, g) mruczy swoją ulubioną mruczankę, h) przyszła zima zła.

5. Ustal symbole kategorialne następujących wyrażeń dobierając odpowiedni kontekst: a) pod , b) zanim, c) pobiegł, d) wolno, e) pada śnieg, f) student kulturoznawstwa, g)nerwowo, h) albo

6. Podaj przykłady kontekstów, a na tej podstawie podaj zapis kategorii danych funktorów dla następujących przykładów (liczba w nawiasie oznacza ilość możliwych kategorii): a) czyta (2) , b) ich (2) , c) nie (3), d) choć (3),

6. Sprawdź poprawność wyrażenia stosując test poprawności:

a) Długa wypowiedź wymaga sprawdzenia poprawności stylistycznej.

b) Himalaje stale pochłaniają wiele ofiar .

c) Obiady w stołówce studenckiej są smaczne, ale nie tanie.

d) Kierowca miał wypadek, bo jezdnia była śliska.

Materiały 2

Podaj schemat zdaniowy zdań:

1. Jeżeli Warszawa jest stolicą Polski to albo Rzym albo Warszawa jest stolicą Polski

2. Jeżeli otrzymałem fałszywy wniosek to przyjąłem fałszywe założenia lub zrobiłem błąd w rozumowaniu.

3. Twoja wypowiedź jest prawdziwa wtedy i tylko wtedy gdy używasz ogólnie przyjętej argumentacji.

4. Jeżeli krótkie zdanie zawiera jasno wyrażoną myśl to nieprawda, że zdanie wielokrotnie złożone zawiera myśli wyrażone niejasno.

5. Nieprawda, że uczyłeś się systematycznie i nie umiesz.

6. Kochasz mnie lub mnie nie kochasz.

7. Jeżeli w naukach humanistycznych każdą tezę można uznać równocześnie za prawdziwą lub fałszywą w zależności od elokwencji jej propagatora to nauki humanistyczne nie są nauką przez duże N lub w naukach humanistycznych należy przyjąć pozalogiczne kryteria prawdziwości.

8. Ukończę studia i będę pracować naukowo lub zostanę nauczycielem albo dziennikarzem.

Problemy

Zad 1. Napisz schematyczny zapis następujących zdań:

1. Jeżeli kulturoznawstwo nie jest nauką o kulturze to pojęcie kultury nie istnieje lub kulturoznawstwo nie jest nauką.

2. Studenci polonistyki doskonale znają zasady polskiej ortografii oraz polskiej stylistyki wtedy i tylko wtedy, gdy nie unikają zajęć z przedmiotów językoznawczych i nie czytują prasy codziennej.

3. Korkociąg jest dobry dla lotników, my marynarze musimy odbijać. ( J. Przybora).

4. Jak nie wiecie z czym przyszliście, to wracajcie do domu - [...] tam wam się przypomni, jeżeli co ważnego. (J. Przybora)

5. Nieprawda, że spory filozoficzne powstają zawsze i tylko wtedy, gdy nauka przeżywa kryzys lub rozwija się zbyt gwałtownie.

6. Nie jest prawdą, że jeżeli teoria Ensteina jest bardziej uniwersalna to teoria Newtona jest bez wartości.

7. Przeczytam kilka podręczników logiki lub wysłucham kilku wykładów i rozwiążę wszystkie zadania - wtedy zdam egzamin.

8. Ukończę studia i będę pracować naukowo lub zostanę nauczycielem i będę zadowolony/na wtedy i tylko wtedy gdy bogato się ożenię/wyjdę za mąż.

9. Jeżeli czytasz swobodnie w obcym języku, to o ile nie potrafisz w nim mówić, to znasz go biernie.

10. Zaakceptujesz zajęcia z logiki i uznasz, że jest ona łatwo przyswajalna, jeśli nie masz złych wspomnień z lekcji matematyki w szkole średniej.

Zad. 2 Sformułuj w sposób stylistycznie poprawny i jednoznaczny zdania powstające z podanych niżej schematów przez podstawienie:

p - "medycyna niekonwencjonalna jest działem medycyny jako nauki"

q - "za medycyną niekonwencjonalną świadczą pozytywne wyniki jej stosowania"

r - "przeciw medycynie niekonwencjonalnej świadczy jej nieskuteczność"

p (q r), b) p (q r), c) (q r) p, d) p (q r), e) q (p r),

f) (q r) p, g) [p (q r)]

Materiały 3

1. Przykład

- prawo de Morgana dla alternatywy

- prawo de Morgana dla koniunkcji

- prawo zaprzeczenia implikacji

a) (p → q) → [(p → s) →(p → q ∧ s)] ; b) [(p ∨ q) ∧ (p → r) ∧ (q → r)] → r ; c) [(~q) → p] → (p ∨ q) ;

d) [(p ∨ q) ∧ (p → r) ∧ (q → s)] → (r ∨ s) ; e) [(~p ∨ ~q) ∧ (r → p) ∧ (r → q)] → ~r ;

f) [(~p ∨ ~q) ∧ (r → p) ∧ (s → q)] → (~r ∨ ~s) ; g) [(~p) → q] → (p ∨ q)

Problemy

1. Oceń zdanie wstawiając za p, q, r, s zdania fałszywe lub prawdziwe aż do uzyskania zdania fałszywego. Wskaż tautologie.

a)
, b)
, c)
, d)
,

e)
, f)
,

g)
, h)
, i)
, j)

k)
, l)
, m)

n)
, o)
, p)
, r)

s)
, t)
, u)
,

v)
, w)
, x)

2. Wiadomo, że prawdziwe jest zdanie:

“Nieprawda, że jeżeli nauki humanistyczne są interesujące, to jeżeli polonistyka jest nauką humanistyczną to polonistyka nie jest nauką interesującą.” Czy na podstawie tego zdania potrafimy odpowiedzieć na pytania:

a) Czy nauki humanistyczne są interesujące ?

b) Czy polonistyka jest nauką humanistyczną ?

c) Czy polonistyka jest nauką interesującą ?

3. Podaj matrycę logiczną funktora alternatywy rozłącznej „albo .... albo” () oraz binegacji „ani ...ani” (#)

4. Sprawdź, czy dane zdanie jest kontrtautologią.

a)
, b)
, c)

Materiały 4

Przykład

1. Gdyby Frodo przekazał pierścień Gandalfowi to pierścień zostałby zniszczony. Gdyby Frodo przekazał pierścień Borowmirowi to pierścień nie zostałby zniszczony. Ale pierścień został zniszczony, zatem Frodo przekazał pierścień Gandalfowi.

2. Gdyby Frodo przekazał pierścień Gandalfowi to pierścień zostałby zniszczony. Gdyby Frodo przekazał pierścień Borowmirowi to pierścień nie zostałby zniszczony. Ale pierścień został zniszczony, zatem Frodo nie przekazał pierścienia Borowmirowi.

3. Jeśli poseł A spowoduje wypadek samochodowy pod wpływem alkoholu to zostanie pozbawiony immunitetu. Jeśli zostanie pozbawiony immunitetu to pójdzie do więzienia i utraci prawo jazdy. Poseł A został pozbawiony immunitetu. Zatem poseł A utraci prawo jazdy.

3a. Jeśli poseł A spowoduje wypadek samochodowy pod wpływem alkoholu to zostanie pozbawiony immunitetu. Jeśli spowoduje wypadek pod wpływem alkoholu i zostanie pozbawiony immunitetu to pójdzie do więzienia i utraci prawo jazdy. Poseł A został pozbawiony immunitetu. Zatem poseł A utraci prawo jazdy.

4. Gdyby partia A weszła w koalicję z partią B i partia uzyskała wpływy w rządzie to partia B będzie miała wpływy w rządzie. Gdyby partia A nie weszła w koalicję z partią B i partia B uzyskała wpływy w rządzie to partia A nie uzyska wpływów w rządzie. Partia A uzyskała wpływy w rządzie. Zatem partia B uzyskała wpływy w rządzie.

5. Gdyby partia A weszła w koalicję z partią B i partia uzyskała wpływy w rządzie to partia B będzie miała wpływy w rządzie. Gdyby partia A nie weszła w koalicję z partią B i partia B uzyskała wpływy w rządzie to partia A nie uzyska wpływów w rządzie. Obie partie uzyskały wpływy w rządzie. Zatem partia A weszła w koalicję z partią B.

6. Jeśli Pan Z nie będzie popierał w wyborach Pana A to straci stanowisko w Radzie Nadzorczej. Jeśli straci stanowisko to straci służbowy samochód. Jeśli będzie popierał Pana A to straci autorytet. Zatem Pan Z straci samochód lub autorytet.

7. Jeśli Pan Z nie będzie popierał w wyborach Pana A, to straci stanowisko i służbowy samochód. Jeśli będzie popierał Pana A, to straci autorytet. Jednak Pan Z nie stracił samochodu i autorytetu. Zatem nie warto uczyć się logiki.

8. Oskarżony popełnił zbrodnię. Jeśli oskarżony popełnił zbrodnię to zostanie ukarany. Zatem oskarżony zostanie ukarany.

9. Jeśli lekarstwo było skuteczne, to chory wyzdrowiał. Chory wyzdrowiał. Zatem lekarstwo było skuteczne.

10. Oskarżony był na miejscu zbrodni. Nieprawda, że równocześnie oskarżony był na miejscu zbrodni i popełnił zbrodnię. Zatem oskarżony nie popełnił zbrodni.

11. Świadek nie kłamie. Świadek lub oskarżony kłamie. Zatem oskarżony kłamie.

12. Oskarżony nie był na miejscu zbrodni. Gdyby oskarżony popełnił zbrodnię to byłby na miejscu zbrodni. Zatem oskarżony nie popełnił zbrodni.

13. Gdyby oskarżony przyniósł ze sobie narzędzie zbrodni to oskarżony zamierzałby popełnić zbrodnię. Ale oskarżony nie przyniósł ze sobą narzędzia zbrodni. Zatem oskarżony nie zamierzał popełnić zbrodni.

14. Jeśli rozumujesz poprawnie, to dochodzisz do prawdziwych konkluzji. Nie rozumujesz poprawnie. Zatem nie dochodzisz do prawdziwych konkluzji.

PrzykładyZbadaj, jakie związki logiczne zachodzą między podanymi poniżej zdaniami :1) Jeśli oskarżony był na miejscu przestępstwa to oskarżony nie popełnił przestępstwa.

2) Oskarżony był na miejscu przestępstwa lub oskarżony popełnił przestępstwo.

3) Albo oskarżony nie był na miejscu przestępstwa albo oskarżony nie popełnił przestępstwa.

4) Jeśli oskarżony popełnił przestępstwo to oskarżony był na miejscu przestępstwa .

5) Nie jest prawdą, że ani oskarżony nie był na miejscu przestępstwa ani oskarżony nie popełnił przestępstwa.

6) Oskarżony nie był na miejscu przestępstwa i oskarżony popełnił przestępstwo.

7) Oskarżony był na miejscu przestępstwa lecz oskarżony nie popełnił przestępstwa.

8) Nie jest prawdą, że jeśli oskarżony był na miejscu przestępstwa to oskarżony popełnił przestępstwo.

9) Ani oskarżony nie był na miejscu przestępstwa ani oskarżony nie popełnił przestępstwa.

10) Oskarżony był na miejscu przestępstwa, a skoro oskarżony był na miejscu przestępstwa to oskarżony popełnił przestępstwo.

11) Nie jest prawdą, że albo oskarżony był na miejscu przestępstwa, albo oskarżony nie popełnił przestępstwa.

Materiały 5

I) Zbadaj poprawność przedstawionych wnioskowań:

1. Jeżeli A jest konformistą, to postępuje zgodnie z własnymi przekonaniami tylko wtedy, gdy jest pewny swej prawomyślności. Jeżeli A jest bardzo młody to nie jest konformistą. Zatem jeśli A jest bardzo młody, to postępuje zgodnie z własnymi przekonaniami, choćby nawet nie był pewny swej prawomyślności.

2. Jeśli A mówi nieprawdę, to dokładnie jedno z dwojga: myli się lub kłamie. Jeśli kłamie, to co najmniej jedno z dwojga: ma coś do zyskania lub coś do stracenia. Lecz A nie myli się, a przy tym nie ma nic do zyskania. Zatem co najwyżej jedno z dwojga: A mówi nieprawdę lub nie ma nic do stracenia.

3. Jeśli Pan Z nie będzie głosował na swego przełożonego - Pana A to straci stanowisko. Jeśli straci stanowisko to straci służbowy samochód. Jeśli będzie głosował na Pana A to straci autorytet. Zatem Pan Z straci albo samochód albo autorytet.

4. Gdyby Pan Z nie głosował na swego przełożonego - Pana A to straciłby stanowisko i służbowy samochód. Jeśli głosowałby na Pana A to straciłby autorytet. Jednak Pan Z nie stracił ani samochodu ani autorytetu. Zatem Bóg istnieje.

5. Jan jest podwładnym Piotra. Jeśli Jan jest inteligentniejszy od Piotra, a jest jego podwładnym, to Piotr czuje się zagrożony. Lecz Jan nie jest inteligentniejszy od Piotra. Zatem Piotr nie czuje się zagrożony.

6) Jan jest podwładnym Piotra. Jeśli Jan jest inteligentniejszy od Piotra, a jest jego podwładnym, to Piotr czuje się zagrożony. Lecz Piotr nie czuje się zagrożony. Zatem Jan nie jest inteligentniejszy od Piotra.

7) Jan jest podwładnym Piotra. Jeśli Jan jest inteligentniejszy od Piotra, a jest jego podwładnym, to Piotr czuje się zagrożony. A Piotr czuje się rzeczywiście zagrożony. Zatem Jan jest inteligentniejszy od Piotra.

8) Jan jest inteligentniejszy od Piotra. Jeśli Jan jest inteligentniejszy od Piotra, to gdyby Jan był jego podwładnym, to Piotr czułby się zagrożony. Zatem Jan nie jest podwładnym Piotra.

II) Wskaż zdania synonimiczne, porównując ze sobą zdania od a) do j):

a) Jeżeli medycyna szamańska jest sztuką, to nie jest nauką.

b) Jeżeli medycyna szamańska nie jest nauką, to jest sztuką.

c) Medycyna szamańska nie jest nauką, lecz sztuką.

d) Medycyna szamańska jest nauką zawsze i tylko, gdy nie jest sztuką.

e) Medycyna szamańska jest nauką i sztuką zarazem.

f) Medycyna szamańska nie jest ani nauką, ani sztuką.

g) Co najmniej jedno z dwojga: medycyna szamańska jest nauką lub sztuką.

h) Co najwyżej jedno z dwojga: medycyna szamańska jest nauką lub sztuką.

i) Dokładnie jedno z dwojga: medycyna szamańska jest nauką lub sztuką.

j) Medycyna szamańska nie jest nauką.

Materiały 6

1. Dane są zbiory A = {a,b,c,d,e} i B = {d,e,f,g,h} zawarte w zbiorze X = {a,b,c,d,e,f,g,h,i,j,k}. Wyznacz zbiory A'; B'; A∪B; A∩B; A\B; B\A. Przykład

2. A - zbiór wszystkich ludzi P₁ - podział na kobiety i mężczyzn - P₁ = {K,M} P₂ - podział na palących i niepalących - P₂ = {P,NP}

P₃ - podział na pracujących i niepracujących - P₃ = {Z,NZ}. Wyznacz podział właściwy podstawowych jednostek klasyfikacyjnych opartych na trójstopniowej klasyfikacji K₃ = {A: P₁; P₂; P₃}

Problemy

1. Ile elementów mają zbiory: a)
, b)
, c)
, d)
, e)
.

2. Wyznacz zbiory A ∪ B, A ∩ B, A - B oraz B - A, jeśli: a) A={a,b,c,d,e}, B={c,d,f,g,h}. b) A = {-1, 0, 1, 2}, B = {-4, -3, -1, 2, 3}.

c) A = {-4, -2, 0, 2}, B = {1, 3, 5, 7}, d) A = { 1, 2, 3, 4, 5}, B = {5, 4, 3, 2, 1 }.

3. Niech
. Wyznacz zbiory
gdy

a) A={1,2,3,4,5,6}, B={4,5,6,7,8}, C={6,7,8,9}, X={0,1,2,3,4,5,6,7,8,9,10,11}

b) A={0,1, 2, -2, 3, 4 , - 4,5, -6}, B={4, - 5,6,7, - 7, 8}, C={-6, - 7,8,9},

X={0,1 -1,2, -2, 3, -3, 4, -4 , 5 , - 5, 6, - 6, 7, - 7, 8, - 8, 9, -9, 10, - 10, 11, - 11}.

4. A - zbiór kobiet, B - zbiór osób palących papierosy. Przyjmując za zbiór maksymalny - zbiór wszystkich ludzi na Ziemi opisz następujące zbiory. a) A', b) B' , c)
, d)
, e)
, f) A - B, g) A' - B', h) B' - (A ∪B') .

5. Dokonaj dowolnej trzystopniowej klasyfikacji zbioru polskich miast.

Materiały 7

1. Określić dziedzinę i przeciwdziedzinę oraz pole relacji a) R₁ (x,y) - "x jest siostrą y", b) R₂ (x,y) - "x jest krewnym y", c) R₃ (x,y) - "x jest powinowatym y" w U = {O,M,W,S,C(sO),C(sM), B₁ , B₂ , S₁ , S₂ }.

2. Jakie zależności są między relacjami P(x,y) - "x nie jest młodszy od y" określonej w zbiorze ludzi U relacji R(x,y) - "x jest starszy od y", relacji S(x,y) - "x jest w tym samym wieku co y" oraz T(x,y) - "x jest młodszy od y".

3. Zbadać własności relacji: R₁(x;y) - x jest wyższy od y, R₂(x;y) - x jest wyższy od y lub tego samego wzrostu co y, R₃(x;y) - x tego samego wzrostu co y w zbiorze U = {A - wzrost 180 cm; B - wzrost 185 cm; C - wzrost 180 cm; D - wzrost 190 cm; E - wzrost 190 cm}.

Określić zależności między tymi relacjami.

Problemy

1. Określić zbadaj własności następujących relacji R(x,y), ich dziedzinę i przeciwdziedzinę oraz pole, gdy (U - zbiór wszystkich ludzi na Ziemi): a) R(x,y) - "x jest matką y", b) R(x,y) - "x jest starsza/starszy od y", c) R(x,y) - "x jest zwierzchnikiem y"

2) Określić zbadaj własności następujących relacji R(x,y), ich dziedzinę i przeciwdziedzinę oraz pole, gdy (U - zbiór wszystkich podzbiorów zbioru {a,b,c}) a) R(x,y) - "x zawiera się w y", b) R(x,y) - "x krzyżuje się z y", c) R(x,y) - "x jest rozłączne z y"

3) Przedstaw w postaci sumy, różnicy, iloczynu innych relacji następującą relację ( U - zbiór wszystkich ludzi):

a) zarabia przynajmniej tyle samo, b) szanuje, choć nie lubi, c) jest młodszą siostrą,

4) Określ związki między następującymi relacjami (we wspólnym zbiorze U):

a) jest ojcem --- jest starszy, b) jest bratem --- jest ojcem, c) jest przełożonym --- zarabia więcej .

Materiały 8

1. Stosując diagramy Venna ustal relacje między nazwami: a) student - 20 letni mężczyzna, b) gruszka - nie warzywo, c) miasto - państwo, d) ktoś kto czyta książki naukowe lub książeczkę czekową - ktoś kto czyta książki i książkę telefoniczną, ale nie czyta książeczki czekowej, e) kobieta - niewiasta, f) student - analfabeta, g) awantura - kłótnia.

2. Zbadaj poprawność następujących definicji analitycznych a) Tramwaj to elektryczny pojazd szynowy., b) Panna to niezamężna dorosła kobieta., c) Naukowiec to pracownik wyższej uczelni, d) Soczewka, to przedmiot ze szkła skupiający wiązkę równoległych promieni świetlnych., e) Ryba jest to zwierzę wodne oddychające skrzelami.

Materiały 9

1. Odczytaj zdanie a) , gdy Q - być piękną/ym, R - być mądrą/ym. b) , gdy P - być nudnym i Q - być formą zajęć dydaktycznych, x - kolejne ćwiczenia z logiki. c. Odczytaj zdanie , gdy P - mieć rodzeństwo, Q - być człowiekiem, R - x jest siostrą y , S - x jest bratem y. d) , gdy P - być szczęśliwym ,Q - być człowiekiem, R - x nienawidzi y , S - x kocha y.

2. Zapisz w postaci kwantyfikatorowej zdanie „Nikt nie przeczytał wszystkich książek”.

3. Sprawdź, czy dana struktura relacyjna jest modelem, czy kontrmodelem formułę zamkniętą ,

a) S₁ = {U, P,Q}, gdzie U - zbiór ludzi, P - x jest synem y, Q - x jest starszy od y; b) S₂ = {U, P,Q}, gdzie U - zbiór liczb naturalnych, P - x jest mniejsza od y, Q - x jest równa y; c) S₃ = {U, P,Q}, gdzie U - zbiór ludzi, P - x jest podwładnym y' Q - x zarabia więcej od y.

Problemy

1. W poniższych formułach wskaż zmienne związane i zmienne wolne (zaznacz zakres działania kwantyfikatora).

a) , b)

2. Podaj kwantyfikatorowe schematy następujących zdań:

a) Każdy student jest humanistą.,

b) Nie wszystko złoto, co się świeci,

c) Każdy kogoś toleruje,

d) Byli tacy filozofowie, którzy nie pozostawili po sobie żadnej teorii filozoficznej,

e) Są zajęcia, których nie lubi żaden student,

f) Pewni studenci traktują poważnie egzamin tylko u niektórych wymagających egzaminatorów,

g) Byli tacy naukowcy, którzy nie napisali żadnej książki.

3. Niech S = {L, R₁ , R₂ } będzie schematem, w którym - L = zbiór ludzi, R₁ (x) := „x jest kobietą”, R₂ (x,y) := „x jest bratem y”. Sprawdź, czy S jest modelem, czy kontrmodelem następujących formuł:

1. ,

2. ,

3. , d).

4. Wskaż reguły, na których oparte są poniższe rozumowania i spróbuj ocenić intuicyjnie (bez stosowania reguł formalnych), czy są one niezawodne:

1. Każdy, kto jest mądrzejszy od wszystkich jest też mądrzejszy od samego siebie. Ale nikt nie jest mądrzejszy od samego siebie. Zatem nikt nie jest mądrzejszy od wszystkich.

2. Niektóre teorie są sprzeczne z innymi teoriami. Jeżeli jakiekolwiek dwie teorie są sprzeczne ze sobą, to co najmniej jedna z nich jest fałszywa. Zatem : niektóre teorie są fałszywe.

c) Każda teoria jest fałszywa wtedy i tylko wtedy gdy jest niezgodna z faktami. Każda teoria wewnętrznie sprzeczna jest niezgodna z faktami. Zatem każda teoria fałszywa jest wewnętrznie sprzeczna.

Materiały 10

Przykłady: Każdy kot jest zwierzęciem. Wszyscy ludzie są szczęśliwi. (Człowiek jest szczęśliwy. - duży kwantyfikator jest domyślny) Nikt nie jest doskonały. Kto pyta o drogę, nie błądzi. Niektóre zwierzęta są udomowione. Bywają jeszcze uczciwi ludzie. Był złodziej, który nie kradł. Są rzeczy, o których nie śniło się filozofom.

1. Sprawdź poprawność wnioskowania:

1. „Nie każdy muzyk jest artystą, zatem są muzycy (młodzieżowi), którzy nie są artystami.”

2. „ Bywają muzycy, którzy są artystami, zatem niektórzy muzycy nie są artystami.”

3. Wszystkie formuły KRZ są formułami KRP. Niektóre formuły KRZ nie są tautologiami. Zatem niektóre formuły KRP nie są tautologiami.

4. Wszystko co jest ze złota jest cenne. Nie wszystko co się świeci jest cenne. Zatem: nie wszystko co się świeci jest ze złota.

5. Żadna ideologia nie jest pożyteczna. Żadna pożyteczna rzecz nie jest szkodliwa. Zatem żadna ideologia nie jest szkodliwa.

6. Niektórzy mężczyźni są twórcami w kulturze. Niektórzy twórcy są inteligentni. Zatem niektórzy mężczyźni są inteligentni.

7. „Wszyscy posłowie na sejm RP mają polskie obywatelstwo. Żadna osoba z polskim obywatelstwem nie jest kosmitą. Zatem istnieją kosmici, którzy nie są posłami na sejm RP”.

8. „Wszyscy posłowie na sejm RP mają polskie obywatelstwo. Żadna osoba z polskim obywatelstwem nie jest Chińczykiem. Zatem istnieją Chińczycy, którzy nie są posłami na sejm RP”.

Problemy

1. Sprawdź poprawność dla następujących wnioskowań :

1. Nie wszyscy politycy są kłamcami. Zatem niektórzy politycy nie są kłamcami.

2. Nie wszyscy politycy są kłamcami. Zatem niektórzy politycy są kłamcami.

3. Nie wszyscy politycy są kłamcami. Zatem niektórzy kłamcy są politykami.

4. Niektóre twierdzenia nauki są zdaniami fałszywymi. Zatem niektóre zdania fałszywe są twierdzeniami nauki.

E) Niektóre twierdzenia nauki są zdaniami fałszywymi. Zatem nie jest tak, że żadne twierdzeniami nauki nie jest zdaniem fałszywym.

2. Sprawdź, które pary zdań z wypisanych poniżej są wzajemnie sprzeczne:

1. Każdy student ma dobrą pamięć.

2. Niektórzy studenci mają dobrą pamięć.

3. Nie wszyscy studenci mają dobrą pamięć.

4. Żaden student nie ma dobrej pamięci.

5. Nie jest tak, że niektórzy studenci nie mają dobrej pamięci.

6. Nie jest tak, że niektórzy studenci mają dobrą pamięć.

7. Niektórzy studenci nie mają dobrej pamięci.

8. Nie jest tak, że żaden student nie ma dobrej pamięci.

1. Zbadaj niezawodność poniższych reguł:

a)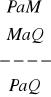
, b)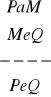
, c)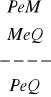
, d)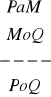
, e)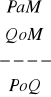
, f)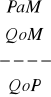

2. Sprawdź poprawność dla następujących wnioskowań :

1. Niektórzy aktorzy są sławni. Wszyscy sławni ludzie są zarozumiali. Zatem niektórzy aktorzy są zarozumiali.

2. Niektórzy aktorzy nie są sławni. Wszyscy sławni ludzie są zarozumiali. Zatem niektórzy aktorzy nie są zarozumiali.

3. Niektórzy aktorzy są sławni. Żaden sławny człowiek nie jest zarozumiały. Zatem nie wszyscy aktorzy są zarozumiali.

4. Niektórzy aktorzy są sławni. Niektórzy sławni ludzie są zarozumiali. Zatem niektórzy aktorzy są zarozumiali.

5. Żaden zając nie jest wilkiem. Żaden wilk nie jest wielbłądem. Zatem żaden zając nie jest wielbłądem.

6. Reklama zawsze powoduje wzrost sprzedaży. Wzrost sprzedaży zawsze powoduje wzrost zysków. Zatem reklama zawsze powoduje wzrost zysków.

7. Reklama nie zawsze powoduje wzrost sprzedaży. Wzrost sprzedaży zawsze powoduje wzrost zysków. Zatem reklama nie zawsze powoduje wzrost zysków.

5. W poniższych regułach dodaj po jednej przesłance tak, aby otrzymać regułę niezawodną:

1. 
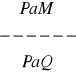
   , b)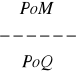
   , c)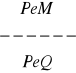
   , d)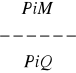
   .

6. W poniższych regułach dodaj założenie o niepustości jednej z nazw tak, aby otrzymać regułę niezawodną:

1. 
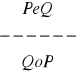
   , b)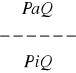
   , c)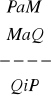
   , d)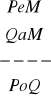
   , e)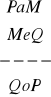
   .

7. Podaj najbardziej prawdopodobną przesłankę w poniższych wnioskowaniach entymematycznych. Sprawdź czy po uzupełnieniu wnioskowania o tę przesłankę wnioskowanie staje się poprawne.

1. Papieże są ludźmi. Zatem papieże są omylni.

2. Papieże są omylni. Zatem papieże są ludźmi.

3. Żaden delfin nie jest rybą. Zatem żaden delfin nie oddycha skrzelami.

4. Żaden delfin nie oddycha skrzelami. Zatem żaden delfin nie jest rybą.

5. Nie wszystko złoto, co się świeci. Zatem nie wszystko cenne, co się świeci.

6. Nie wszystko cenne, co się świeci Zatem nie wszystko złoto, co się świeci.

1

1

Oprac. M. Piętka

---