MOMENT BEZWŁADNOŚCI

Wyrażenie
odgrywa w ruchu obrotowym podobną rolę jak masa w ruchu postępowym. Suma iloczynów mas poszczególnych cząstek bryły i kwadratów ich odległości od osi obrotu jest miarą bezwładności bryły w ruchu obrotowym i nosi nazwę momentu bezwładności względem danej osi obrotu.

I=

W przypadku ciała sztywnego o ciągłym rozkładzie masy możemy podzielić je na małe elementy masy dm i sumowanie we wzorze tym zastępujemy całkowaniem.

I=

Przy czym całkowanie rozciągnięte jest na całą objętość całkowania.

Moment bezwładności ciała zależy nie tylko od wielkości masy wykonującej ruch obrotowy ale także od sposobu rozmieszczenia tej masy wokół osi obrotu. Działając tym samym momentem siły
na bryłę o masie m uzyskamy większe przyspieszenie kątowe ε, gdy masa bryły jest rozmieszczona bliżej osi ( rys. a), mniejsze zaś, gdy masa jest rozmieszczona dalej od osi ( rys b).

Zgodnie z twierdzeniem Steinera: moment bezwładności bryły I względem dowolnej osi jest równy sumie momentu bezwładności I_c tej bryły względem osi równoległej do danej i przechodzącej przez środek masy bryły oraz iloczynu masy bryły i kwadratów odległości między wymienionymi osiami

I = I_c+ md²

Ruch obrotowy bryły opisuje II zasada dynamiki

M= εI

gdzie M- moment wypadkowy wszystkich sił działających na ciało, I- moment bezwładności bryły

Jest to podstawowe prawo ruchu obrotowego. Zgodnie z tym prawem wypadkowy moment siły działającej na ciało obracające się równa się iloczynowi momentu bezwładności względem aktualnej osi obrotu przez przyspieszenie kątowe. Prawo w tej postaci obowiązuje gdy moment bezwładności ciała jest niezmienny w czasie.

Zarówno moment siły jak i moment bezwładności są obliczane względem tej samej osi.

Równianie ε =
jest odpowiednikiem równania II zasady dynamiki w ruchu postępowym a =
. Role przyspieszenia liniowego w ruchu obrotowym bryły odgrywa przyspieszenie kątowe. Rolę siły pełni moment siły, rolę masy- moment bezwładności. Przyspieszenie kątowe ε i moment siły są wielkościami wektorowymi. Są one skierowane wzdłuż osi stałej obrotu i są określone za pomocą iloczynów wektorowych

M = R × F

Zwrot momentu siły określa reguła śruby prawoskrętnej, zatem zmiana kolejności składników w iloczynie wektorowym zmienia zwrot wektora

WYZNACZENIE MOMENTU BEZWŁADNOŚCI ŻYROSKOPU

Żyroskopem lub bąkiem nazywamy masywne, symetryczne ciało sztywne, szybko wirujące względem swej osi symetrii, zwanej osią żyroskopu. Oś żyroskopu jest jedną z głównych osi bryły.

• Jeżeli ta oś jest nieruchoma w przestrzeni to moment pędu bryły wynosi

L = Iω

Ponadto jeśli żyroskop wiruje z prędkością kątową ω względem osi symetrii, to moment pędu L jest wielkością stałą, czyli L = Iω = const

• Jeżeli oś żyroskopu obraca się z pewną prędkością kątową ω to w takim przypadku wypadkowe obroty żyroskopu zachodzą wokół osi, która nie pokrywa się z osią symetrii, a kierunek wektora
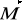
  nie jest zgodny z kierunkiem osi bąka.

Moment siły ciężkości żyroskopu względem środka masy jest równy zero.

W przypadku gdy na żyroskop działa zewnętrzny moment siły
prostopadły do osi obrotu żyroskopu to wówczas zewnętrzny moment siły
powoduje zmianę wektora momentu pędu d
w czasie dt

Zmiana wektora momentu pędu d
jest prostopadła do momentu pędu
. Wektor
w czasie dt zakreśli kąt dφ.

Wówczas obserwujemy zjawisko precesji. Jest to ruch osi obrotu żyroskopu wokół osi pionowej z prędkością kątową ω₁ prostopadłą do osi obrotu.

ω =

Z rysunku wynika d
×
. Po podzieleniu obustronnie przez czas dt otrzymamy
×
. Po podstawieniu do wzoru
wcześniejszej wartości otrzymamy
×
. Jeśli zewnętrzny moment siły ma stałą wartość to prędkość kątowa precesji ω₁ jest stała. Zgodnie z pierwszą zasadą dynamiki dla ruchu obrotowego, suma wszystkich sił działających na obracający się żyroskop musi równać się zeru.

Moment sił zewnętrznych
jest równoważony przez moment siły bezwładności, zwany momentem żyroskopowym

+
= 0

Z równania
×
wynika M -
×
= 0 czyli

= -
×
=
×

Moment sił żyroskopowych występuje też wtedy, gdy swobodny żyroskop znajduje się w układzie obracającym się z prędkością kątową
. Żyroskop stara się ustawić oś swego obrotu w poziomie aby moment sił żyroskopowych był równy zero. W modelu żyroskopu na przedłużeniu jego osi obrotu znajduje się ciężarek o masie m, który można przesuwać wzdłuż tej osi. Jeśli przesuniemy go o odległość r od położenia w którym żyroskop był zrównoważony to na żyroskop będzie działał moment siły tego ciężarka

=
×
= m
×

Żyroskop będzie wykonywał precesje z prędkością kątową

m
×
=
×
= I
×

W związku z tym że
jest prostopadłe do
, a
jest prostopadłe do
to

mrg = I

stąd moment bezwładności żyroskopu wynosi

I =

---