1. WSTĘP TEORETYCZNY

Lepkość cieczy jest wynikiem sił tarcia wewnętrznego pomiędzy cząsteczkami cieczy.
Siły takie powstają przy ruchu jednej warstwy cieczy wzdłuż drugiej. Jest ono wynikiem oddziaływań międzycząsteczkowych (sił van der Waalsa). Jest to wynikiem jakby zazębienia za pomocą cząsteczek, które przechodzą z jednej warstwy do drugiej przez pomyślane powierzchnie dzielące.

Poruszająca się cząsteczka pociąga za sobą cząstkę z nią sąsiadującą tym silniej im ciecz jest bardziej lepka. Natomiast cząstka pozostająca w spoczynku hamuje poruszające się cząstki sąsiednie. Kiedy ciało porusza się względem nieruchomej cieczy lepkiej, to warstwy cieczy przylegające do ciała pociągają warstwy cieczy względem siebie i na skutek tego siła oporu przeciwdziała ruchowi ciała.

Siłę hamującą
_T można wyrazić następującym wzorem

_T = η S

prawo Newtona

_T - siła tarcia

x - współrzędna osi prostopadłej do kierunku ruchu

- gradient prędkości w tym ruchu

S - powierzchnia przylegania dwóch sąsiadujących warstw

η - współczynnik proporcjonalności pełniący tu rolę współczynnika lepkości dynamicznej

Korzystając z powyższego wzoru można wyprowadzić wzór, zwany prawem Poiseuille'a

Wzór ten podaje, jaka objętość cieczy o współczynniku lepkości η przepływa w czasie t przez rurę o promieniu  R i długości  l, przy różnicy ciśnień na końcach rury  p₁-p₂
Korzystając z tego wzoru, można określić wielkość siły tarcia na jakie napotyka ciecz płynąca w rurze z średnią prędkością cząsteczek v_śr w przypadku przepływu laminarnego. Siła ta hamuje prędkość przepływu cieczy.
Wzór ten ma postać:

Z lepkością cieczy wiąże się też zjawisko hamowania ruchu ciał poruszających się w lepkiej cieczy.

Siłę tę opisuje prawo Stokesa:

Korzystając z tego wzoru, można wyprowadzić wzór na prędkość kulki spadającej w lepkiej cieczy.

Jest to wzór wyjściowy do doświadczalnego wyznaczenia współczynnika lepkości dynamicznej.

Korzystając z podanego wyżej wzoru można wyznaczyć współczynnik lepkości z zależności:

We wzorze nie występuje prędkość kulki. Wyznaczamy ją mierząc czas opadania t na znanym odcinku drogi h (v=
)

2. PRZEBIEG ĆWICZENIA:

Zestaw pomiarowy

Wykonywane czynności:

• mierzymy promienie kilku kulek o podobnych wymiarach i obliczmy ich średnie promienie,

• kulki wrzucamy kolejno do cylindra z gliceryną i mierzymy czas opadania na zaznaczonym odcinku h,

• pomiaru dokonujemy 5 razy;

2.1 OBLICZENIA I ANALIZA BŁĘDÓW:

Dane:

• g =9.81 [m/s²]

• ρ_C = 1.26*10³ [kg/m³] - gęstość gliceryny

• ρ = 7.8*10³ [kg/m³] - gęstość stalowej kulki

• R = 27.03 [mm] - promień cliyndra

• t -czas opadania kulki na wysokości h

Kulka o promieniu r = 1.00[mm]

Lp.	R[mm]	h[m]	t[s]
1.	27.03	0.41	2.69
2.					2.64
3.					2.68
4.					2.64
5.					2.67
średnia				2.66±0,02

S=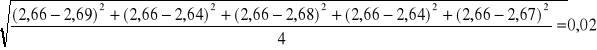

Kulka o promieniu r = 1.90[mm]

Lp.	R[mm]	h[m]	t[s]
1.	27.03	0.41	1.93
2.					1.93
3.					1.89
4.					1.91
5.					1.92
średnia				1.92±0,02

S=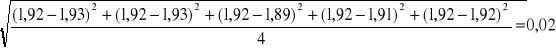

Kulka o promieniu r = 2.40[mm]

Lp.	R[mm]	h[m]	t[s]
1.	27.03	0.41	1.39
2.					1.40
3.					1.39
4.					1.38
5.					1.39
średnia				1.39±0,01

S=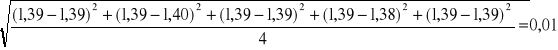

Kulka o promieniu r = 3.10[mm]

Lp.	R[mm]	h[m]	t[s]
1.	27.03	0.41	1.02
2.					1.03
3.					1.02
4.					1.02
5.					1.02
średnia				1.02±0,01

S=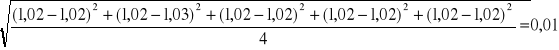

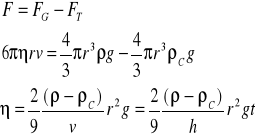
Teraz możemy obliczyć η dla wysokości równej h:

r[mm]	G[m/s^2]	ρ [kg/m^3]	ρc [kg/m^3]	tśr.[s]	η [Pa*s]
1.00 0.05	9.81	7800.00	1260.00	2.66	0.20
1.90 0.05							1.92	0.24
2.40 0.05							1.39	0.28
3.10 0.05							1.02	0.34
średnia							-------------	0.27

Ponieważ ścianki wpływają na ruch kulki przyjmujemy poprawkę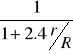
gdzie r oznacza tu promień kulki, a R promień cylindra, w którym opada kulka.

R[mm]	r[mm]	η [Pa*s]	poprawka	η po poprawce
27.03 0.05	1.00 0.05	0.20	0.92	0.18
		1.90 0.05	0.24	0.86	0.21
		2.40 0.05	0.28	0.82	0.23
		3.10 0.05	0.34	0.78	0.27
średnia		0.26		0.22

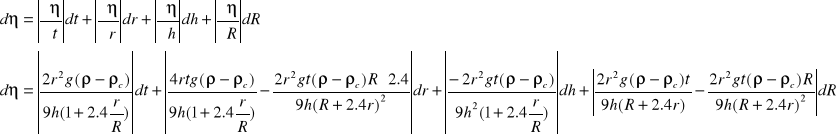
dR = 0.00005 [m]

dr = 0.00005 [m]

dt = 0.2 [s]

dh = 0.01 [m]

Lp.	η [Pa*s]	dη
1	0.18	0,03
2	0.21	0,03
3	0.23	0,04
4	0.27	0,05

Z tych wartości można obliczyć odchylenie standardowe:

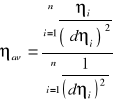
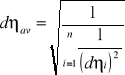
więc:

η=0.21±0.01 [Pa*s]

5. WNIOSKI:

• błędy pomiarów spowodowane są niedokładnym pomiarem czasu opadania kulki,

• prędkość kulek jest uzależniona od ich promienia w tej samej cieczy (mniejsze kulki poruszają się z mniejsza prędkością, większe z większą prędkością),

• dla cieczy newtonowskich lepkość η jest niezależna od prędkości v i siły F,

• poziom gliceryny w cylindrze był zbyt niski żeby można było zmierzyć czas dla dwóch długości więc pomiaru dokonaliśmy tylko dla długości pomiędzy punktem

2 i 3;

h

statyw

korek spustowy

gliceryna

cylinder

1

2

3

---