Wyznaczanie współczynnika lepkości cieczy metodą Stokes'a .

(102)

OPIS TEORETYCZNY

W wielu przypadkach ciecze rzeczywiste zachowują się w przyblizeniu jak ciecz doskonała, tzn. nielepka i nieściśliwa. Dla cieczy nieściśliwej słuszne jest prawo ciągłości przepływu. Wynika z niego, że rurze ciecz osiąga największą prędkość w miejscach o małej powierzchni przekroju.
Z drugiej strony prędkość cieczy w rurze zależy od ciśnień: statycznego i hydrodynamicznego, o czym mówi równanie Bernoulliego.
Oba te prawa nie uwzględniają różnicy prędkości cząsteczek cieczy znajdujących się w różnej odległości od ścianek rury, gdyż nie uwzględniają tarcia między cząsteczkami cieczy, tzw. tarcia wewnętrznego.
Wskutek tarcia wystepującego między cząsteczkami cieczy, poruszająca się cząsteczka pociąga za sobą sąsiadujące cząsteczki tym silniej, im większa jest siła lepkości. Te cząsteczki pociągają następne itd... Każda następna warstwa porusza się jednak nieco wolniej, tym wolniej, im mniejsza lepkość cieczy. Prędkość spada do zera dla cząstek przy ściankach, które są jakby "przyklejone", a więc nieruchome.Tak więc maksymalną prędkość mają cząsteczki na osi rury, jak pokazuje to rysunek:

Taka sytuacja ma miejsce przy małych prędkościach cieczy przez gładką rurę. Mówimy, że przepływ jest laminarny, czyli warstwowy. Kolejne warstwy cieczy płyną nie zakłócając się wzajemnie.
Prędkość cząsteczek przepływających przez dany punkt jest zawsze taka sama.
Przy dużych prędkościach w cieczy popjawiają się zawirowania i ruch z laminarnego zmienia się w turbulentny. W takim ruchu prędkość cząsteczek w każdym punkcie zmienia się nieustannie. Można jednak określić w każdym punkcie pewną prędkość średnią. Rozkład tych prędkości jest wtedy nieco inny:

Do określenia lepkości cieczy posłużymy się takim modelem:

Płaską deseczkę leżąca na powierzchni cieczy w szerokim, płytkim naczyniu, ciągniemy siłą F, nadając jej stałą prędkość v₀. Warstwa cieczy przylegająca do deseczki ma prędkość taką samą jak deseczka, a kolejne, leżące coraz głębiej warstwy, mają prędkości coraz mniejsze. Warstwa cieczy przylegająca do dna jest nieruchoma. Zatem im płytsze naczynie, tym szybciej maleje wraz z głębokością prędkość cieczy.
Z doświadczenia wynika, że wielkość tych zmian powiązna jest z działającą siłą zależnością:

lub ogólniej

S to powierzchnia deseczki,

to takzwany gradient prędkości, czyli zmiana wartości prędkości weraz z głębokością x,

to współczynnik proporcjonalności pełniący tu rolę współczynnika lepkości dynamicznej
Korzystając z powyższego wzoru można wyprowadzić wzór, zwany prawem Poiseuille'a

Wzór ten podaje, jaka objętość cieczy o współczynniku lepkości
przepływa w czasie t przez rurę o promieniu  R i długości  l, przy różnicy ciśnień na końcach rury  p₁-p₂
Korzystając z tego wzoru, można określić wielkość siły tarcia na jakie napotyka ciecz płynąca w rurze z średnią pędkością cząsteczek v_śr w przypadku przepływu laminarnego. Siła ta hamuje prędkość przepływu cieczy.
Wzór ten ma postać:

Zlepkością cieczy wiąże się też zjawisko hamowania ruchu ciał poruszających się w lepkiej cieczy.
W przypadku gdy ciałem tym jest kulka, poruszająca się na tyle wolno, aby opływ cieczy był laminarny

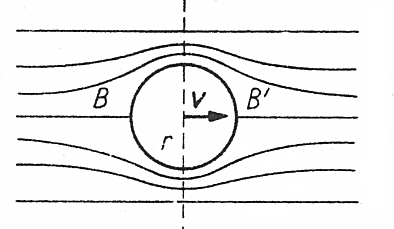
jak na tym rysunku
a nie turbulentny

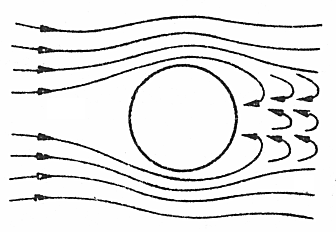
jak na tym rysunku
Siłę tę opisuje prawo Stokesa:

Korzystając z tego wzoru, można łatwo wyprowadzić wzór na prędkość kulki spadającej w lepkiej cieczy.

Jest to wzór wyjściowy do doświadczalnego wyznaczenia współczynnika lepkości dynamicznej.

CEL ĆWICZENIA

Celem ćwiczenia jest wyznaczenie współczynnika lepkości dynamicznej cieczy w oparciu o badanie spadku kulek ołowianych w badanej cieczy.

METODA POMIAROWA

Korzystając z podanego wyżej wzoru można wyznaczyć współczynnik lepkości z zależności:



We wzorze nie występuje prędkość kulki, gdyż wyznaczamy ją mierząc czas opadania t na znanym odcinku drogi h (
)

Podana powyżej zależność jest słuszna dla naczyń bardzo szerokich. Uwzględniając szerokość naczynia, należy wprowadzić poprawkę, po uwzględnieniu której wzór przyjmie postać: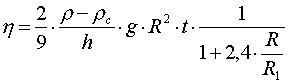



             R oznacza tu promień kulki, a
             R₁ promień cylindra, w którym opada kulka.

OPRACOWANIE WYNIKÓW POMIARÓW

Do doświadczenia wykorzystujemy niewielkie, ołowiane kuleczki. Ponieważ pomiar współczynnika lepkości dla każdej kuleczki indywidualnie byłby dosyć żmudny, zmierzymy przy pomocy mikrometru wymiary (średnice d) partii kulek (10 do 20 szt), wybierzemy te, najmniej różniące się od siebie i przyjmiemy do dalszych pomiarów ich średni promień jako promień R (połowa średniej średnicy). Teraz wrzucamy kolejno (po np. 10 kulek) do każdej rury z badaną cieczą i mierzymy czas opadania każdej kulki na wybranym odcinku h. Miejsce, od którego zaczynamy mierzyć czas opadania kulki nie może być wybrany zbyt blisko powierzchni cieczy. Chodzi o to, aby w momencie pomiaru kulka poruszała się już ruchem jednostajnym.
Wypełnimy tabelkę , np. taką:

Zapisujemy niepewności systematyczne :

R₁= ...        
R= ...         
h= ...        
t= ...
Dodatkowo należy wyznaczyć niepewności przypadkowe dla promienia kulki
R_p i czasu opadania
t_p. Niepewności przypadkowe wyliczymy jako odchylenia standardowe tych wartości od średniej.

(Właściwie
powinno być konsekwentnie oznaczane jako
,   a   
jako
, ale chciałem przez moje oznaczenie podkreślić, że jest to wkład do całkowitego błędu odpowiednio: R  i  t).


Niepewność pomiaru

określimy zgodnie z wzorem na niepewność całkowitą pomiarów pośrednich W tym konkretnym przypadku będzie to wymagało obliczenia kilku pochodnych z funkcji
:









Gdzie


i dokonania wyliczeń według wzoru:

Wysokość h mierzymy tylko raz, możemy więc ocenić tylko jej błąd systematyczny.
Dokładność pomiaru rury podana jest przy ćwiczeniu, jest to więc błąd całkowity (brak trójki w mianowniku przy pochodnej po R₁) Wartości gęstości cieczy i kulki
oraz
₁ należy odczytać z tablic. (Obecnie badanymi cieczami są gliceryna i olej parafinowy, a kulki są ołowiane).

---