Sprawozdanie

Podstawy teoretyczne

Drgania relaksacyjne powstają wskutek wymuszonego wzrostu energii układu oraz jej rozpraszania występujących naprzemiennie, jeśli przy przekazywaniu energii z otoczenia do układu osiąga on stan równowagi nietrwałej. W tym momencie układ może spontanicznie rozproszyć zgromadzoną energię wielokrotnie szybciej niż jest mu przekazywana. W przypadku ciągłego dostarczania energii jej zmiany będą zachodzić periodycznie, gdyż każdorazowo po osiągnięciu stanu równowagi nietrwałej uzyskana energia zostanie rozproszona. Charakterystyczną cechą tych drgań jest przebieg zmian energii. Zmiana energii bowiem, w danej chwili jest proporcjonalna do różnicy między chwilową, a końcową energią układu.

Przekształcając to równanie otrzymamy wyrażenie na chwilową Energię E(t) układu

- podczas rozpraszania energii

• 
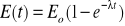
  oraz podczas jej gromadzenia

Otrzymane zależności są funkcjami wykładniczymi.

Wykonanie ćwiczenia

Celem ćwiczenia było zbadanie procesów relaksacyjnych w obwodzie RC.

Drganiem relaksacyjnym w tym obwodzie było cykliczne ładowanie kondensatora prądem stałym i rozładowywanie go. Ponadto do kondensatora przyłączona była równolegle lampa neonowa posiadająca właściwość tzw. kluczowania. Lampę charakteryzują dwie wielkości: napięcie zapłonu U_z i gaśnięcia U_g. Przy napięciu zapłonowym następuje lawinowa jonizacja gazu w lampie (neonówka zapala się). Wtedy przewodność wzrasta o wiele rzędów. Z kolei napięcie gaśnięcia jest wartością przy której zanika jarzenie gazu ( gaz się nie jonizuje). Podczas gdy kondensator był ładowany między jego okładkami powstawała różnica potencjałów. To samo napięcie wystąpiło na lampie. Kiedy osiągnęło wartość U_z, lampa zaczęła się żarzyć, a kondensator zaczął się szybko rozładowywać. Zaczęło więc spadać napięcie na lampie aż przekroczyło U_g i lampa zgasła. Wówczas kondensator ponownie zaczął się ładować. Okres T drgań obwodu jest sumą czasów ładowania t₁ i rozładowania t₂ kondensatora. T= t₁+t₂, gdzie t₁=RC, a t₂=RCln(U_z/U_g). Podczas gromadzenia się ładunku na kondensatorze spełnione jest drugie prawo Kirchoffa ε=IR+q/C, gdzie ε - siła elektromotoryczna (napięcie w zasilaczu), IR - spadek napięcia na oporniku, q/C - spadek napięcia na kondensatorze. Ponieważ natężenie prądu jest pochodną ładunku po czasie, więc podstawiając za I dq/dt i przekształcając odpowiednio równanie otrzymujemy zależność na chwilową wartość ładunku:

gdzie εC = q_k - końcowa wartość ładunku na kondensatorze. Różniczkując to wyrażenie po czasie otrzymamy wzór na chwilowe natężenie prądu w obwodzie:

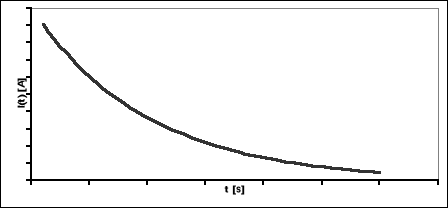
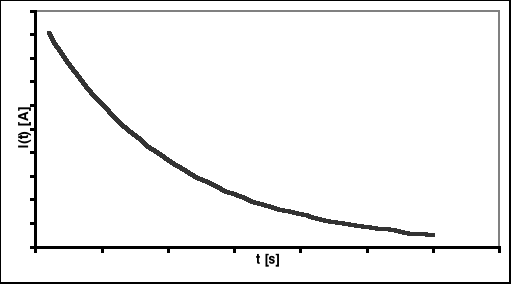
Zależność ta jest funkcją wykładniczą o następującym przebiegu:

Ćwiczenie składało się z trzech etapów:

1. badanie procesu ładowania i rozładowania kondensatora

2. pomiar napięcia zapłonu i gaśnięcia neonówki, przy różnych wartościach R

3. wyznaczenie okresu drgań relaksacyjnych, przy różnych wartościach R i C

Ad 1) Obserwacji podlegał czas ładowania kondensatora prądem stałym.

C=4,7 μF R=3MΩ

Czas [s]	0	5	10		15	20	25	30	35	40
Natężenie prądu [μA]	61	46,3	32,4		22,5	15,6	10,8	7,5	5,1	3,5
Czas połowicznego zaniku T1/2 [s]				10,6

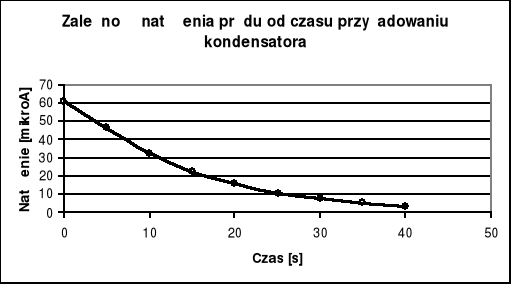
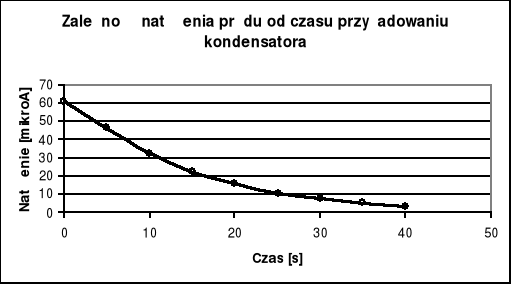
Jak widać otrzymany wykres zbliżony jest do wykresu funkcji wykładniczej, co zgodne jest z założeniami teoretycznymi.

Ad 2) Pomiar napięcia zapłonu i gaśnięcia neonówki

	0,5MΩ	1MΩ	1,5MΩ
Uz [V]	157,0	157,0	156,8
Ug [V]	154,9	155,9	156

Uzśrednie [V]	156,9±0,1
Ugśrednie [V]	154,9±0,4

Ad 3) Pomiar dwudziestu okresów (rozbłysków neonówki), dla różnych wartości C i R

C [μF]	R [MΩ]	t20 [s]	Teksp [s]
4,7	0,5	18	0,9
		1	30	1,5
		1,5	43	2,15
	1,0	0,5	5	0,25
		1	7	0,35
		1,5	10	0,5

Analizując powyższą tabelę łatwo zauważyć, że wraz ze wzrostem oporu i pojemności rośnie okres drgań relaksacyjnych.

Obliczenia

U_zśrednie = (U_z1+U_z2+U_z3)/3=156,9 [V]

U_gśrednie = (U_g1+U_g2+U_g3)/3=155,6 [V]

---