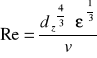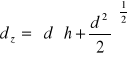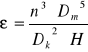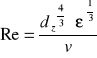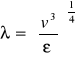Wydział Chemiczny

wpływ energii mieszania na współczynnik wnikania masy w układzie ciało stałe - ciecz

Laboratorium inżynierii chemicznej

Grupa 3

(TCC3055l 0318084)

Środa 13:15-15:45

Opracował:

Dariusz Łozak

Składowe			Punktacja
I	Opracowanie arkusza wyników (schemat aparatury, metodyka badań, wyniki badań), oznaczenia		(0-5), min. 2
II	Przykład obliczeniowy		(0-5), min. 3
III	Wnioski		(0-5), min. 2
∑
Punkty	Ocena
< 8 8 - 9 10 11-12 13 14 15	2.0 3.0 3.5 4.0 4.5 5.0 5.5

Wrocław, 05.04.2006

Oznaczenia:

				pole powierzchni wymiany masy	m^2
				średnica podstawy kształtki	m
		C		stężenie	kg/m^3
		D		średnica	m
		Dab		współczynnik dyfuzji kwasu salicylowego w wodzie	m^2/s
		h		wysokość kształtki	m
		H		wysokość słupa cieczy	m
		m		masa	kg
		n		częstość obrotowa mieszadła	1/s
symbole greckie
	β			współczynnik wnikania masy od powierzchni ciała stałego do wody	m/s
	Δτ			czas zanurzenia kształtek w wodzie	S
	λ			droga, tzw. skala długości Kołmogorowa	m
	υ			lepkość kinematyczna wody	m^2/s
	ε			Ilość energii dostarczanej do układu	m^2/s^3
indeksy górne
*				nasycenia kwasu salicylowego w wodzie
indeksy dolne
	c			cieczy
	d			dysk
	k			końcowa
	K			Kolumny
	m			mieszadła
	P			początkowa
	r			w rdzeniu cieczy
	S			wewnętrzna statora
	t			teoretyczna
	z			zastępcza kształtki

Liczby bezwymiarowe
Liczba Schmidta
Liczba Reynoldsa
Liczba Sherwooda

1. Cel ćwiczenia

Celem ćwiczenia było eksperymentalna wyznaczenie współczynników wnikania masy od odlewanych walców kwasu salicylowego do wody w procesie rozpuszczania tych cząstek w strumieniu cieczy przepływającym przez kolumnę z wirującymi dyskami, oraz porównanie doświadczalnych i obliczonych teoretycznie wartości współczynników wnikania masy.

2. Aparatura

Schemat instalacji badawczej pokazano na rysunku 1 - załącznik A.

3. Metodyka badań

Badania zostały wykonane zgodnie z metodyką zawartą w załączniku A.

4. Wyniki badań

	Masa początkowa	Masa po osuszeniu	Przyrost masy	Wysokość	Średnica
Kształtka 1	4,12g	4,04g	-0,08g	17,6mm	16,4mm
Kształtka 2	8,11g	8,00g	-0,11g	20,2mm	21,4mm
Kształtka 3	17,89g	17,67g	-0,22g	27,5mm	27,3mm
Kształtka 4	28,69g	28,38g	-0,31g	33,1mm	31,2mm

Inne dane:

C = 0

C*= 2,2

υ = 0,998* 10 ^-6

D_ab = 9,08*10 ^-10

D_m = 0,08 m

D_K= 0,2 m

H = 0,55 m

n= 440

5. Metodyka obliczeń - przykład obliczeniowy

5.1 Obliczenia doświadczalnego współczynnika wnikania masy od powierzchni ciała stałego do wody .

1. Średnicę zastępczą kształtki obliczmy korzystając ze wzoru:

(1)

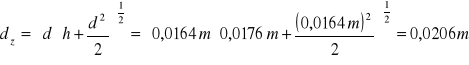
2. Obliczenia powierzchni wymiany masy:

(2)

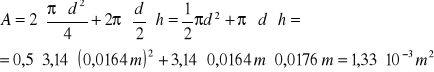
3. Wyznaczanie współczynnika wnikania masy.

(3)

5.2 Obliczenia liczby Sherwooda.

1. Obliczenia energii dostarczonej do układu:

(4)

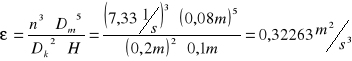
b) Obliczenie liczby Reynoldsa:

(5)

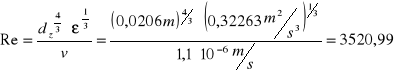
c) Obliczenia drogi - skali długości Kołgomorowa

(6)

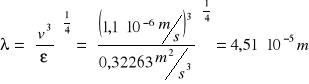
d) Obliczanie liczby Sherwooda

(7)

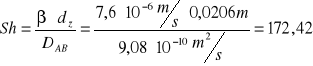
5A. Przykład obliczeniowy dla wartości teoretycznych:

1. Obliczenie liczby Schmidta:

(8)

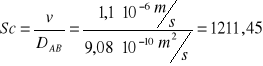
b) Obliczanie liczby Sherwooda:

(9)

2. Obliczanie współczynnika wnikania masy w układzie ciało stałe- ciecz:

(10)

KSZTAŁTKA 1

Średnica zastępcza kształtki	0,0206m
Powierzchnia wymiany masy
Dośw. współczynnik wnikania masy
Energia dostarczona do układu
Liczba Reynoldsa	3520,99
Droga
Dośw. liczba Sherwooda	172,42
Teoretyczna liczba Sherwooda	381,54
Teoretyczny współczynnik wnikania masy
	1,20
	3,55

KSZTAŁTKA 2

Średnica zastępcza kształtki	0,026m
Powierzchnia wymiany masy
Dośw. współczynnik wnikania masy
Energia dostarczona do układu
Liczba Reynoldsa	4802,57
Droga
Dośw. liczba Sherwooda	191,28
Teoretyczna liczba Sherwooda	445,26
Teoretyczny współczynnik wnikania masy
	1,25
	3,68

KSZTAŁTKA 3

Średnica zastępcza kształtki	0,034
Powierzchnia wymiany masy
Dośw. współczynnik wnikania masy
Energia dostarczona do układu
Liczba Reynoldsa	6867,74
Droga
Dośw. liczba Sherwooda	294,69
Teoretyczna liczba Sherwooda	532,06
Teoretyczny współczynnik wnikania masy
	1,44
	3,84

KSZTAŁTKA 4

Średnica zastępcza kształtki	0,039
Powierzchnia wymiany masy
Dośw. współczynnik wnikania masy
Energia dostarczona do układu
Liczba Reynoldsa	8246,35
Droga
Dosw. liczba Sherwooda	345,76
Teoretyczna liczba Sherwooda	582,83
Teoretyczny współczynnik wnikania masy
	1,51
	3,92

WYKRES:

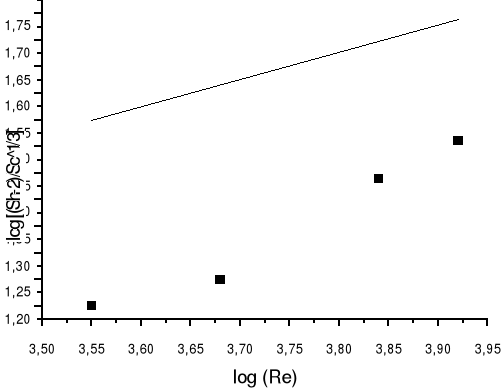
6. Omówienie wyników, wnioski

Dobrze znaną prostą i skuteczną metodą w procesie wymiany masy między ciałem stałym a cieczą jest rozpuszczanie ciał stałych w mieszalnikach.

Szybkość wymiany masy w takim układzie może być zależna od wielu czynników tj:

• parametry geometryczne

• hydrodynamiczne panujących,

• warunki jakie panują w bliskim otoczeniu cząstek ciała stałego.

Liczba Reynoldsa w doświadczeniu opisuje właściwości ciała stałego, nie uwzględniając mieszadła, i jest wyznaczana od prędkości poślizgu cieczy względem cząstki.

Aby poprawnie opisać proces wnikania masy od ciała stałego do cieczy, należy zaznajomić się z warunkami jakie towarzyszą bezpośredniemu otoczeniu cząstki. Ruch płynu jest niezależny od charakteru i geometrii powierzchni jakie ograniczają obszar przepływu. Siły tarcia powodują rozproszenie energii płynu. Obliczanie współczynników wnikania masy z zastosowaniem warunków i parametrów występujących w bliskim otoczeniu cząstki jest obarczone pewnym błędem. Odnosi się on do warunków (nieco innych od ustalonych w rónaniach) przepływu

Teoria izotropii lokalnych burzliwości odwołuje się do stanu, w którym zachodzą fluktuacje burzliwości. Kolejna nieścisłość spowodowana jest trudnością przy doborze odległości d podczas wykonywania doświadczenia. Przyjęta została odległości d, równa rozmiarowi cząstki.

Podczas rozwiązywania równania Sherwooda wykorzystałem założenie: λ<<d.

Wnioski:

Celem doświadczenia było eksperymentalne wyznaczenie ws

półczynników wnikania masy oraz porównanie doświadczalnych obliczonych teoretycznie wartości współczynników. Obie te wartości były wyznaczane dla tych samych warunków.

Otrzymane przeze mnie wyniki:

Dla kształtki 1:

β=

β_t=

Dla kształtki 2:

β=

β_t=

Dla kształtki 3:

β=

β_t=

Dla kształtki 4:

β=

β_t=

Powyższe wartości współczynników nieznacznie się różnią, oznacza to, że popełniony został pewien niewielki błąd. Pomiędzy poszczególnymi wynikami występuje różnica jednego rzędu.

Na wynik doświadczenia miał wpływ rozmiar rozpuszczanych kształtek oraz ilość energii dostarczona do układu ε. Ilość energii zależna była od częstości obrotowej mieszadła, wymiarów mieszadła i mieszalnika- ich średnicy, oraz o wysokości słupa cieczy.

4

---