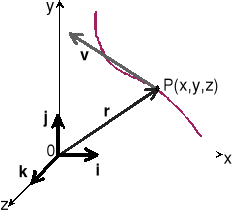
Rys. 1.1. Ruch punktu w układzie XYZ

Prędkość punktu w ruchu postępowym definiuje się następująco:

 
  (1)

gdzie
jest wektorem położenia tego punktu w chwili t w przyjętym układzie odniesienia (rys.1.1). W układzie współrzędnych kartezjańskich wektor
określają trzy składowe x, y, z:

(1a)

gdzie
- wersory (wektory jednostkowe).

Całkowita droga przebyta przez ciało (punkt materialny) w pewnym określonym czasie t:

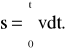
(2)

Prędkość średnia w przedziale czasu (0, t):

(2a)

Przyspieszenie w ruchu postępowym definiujemy następująco:

(3)

Wektor przyspieszenia można rozłożyć na składowe: styczną i normalną (rys. 1.2):

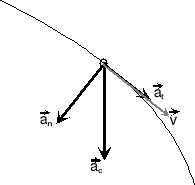
Rys. 1.2. Przyspieszenie nor-malne i styczne

- przyspieszenie styczne:

(4)

- przyspieszenie normalne:

(5)

gdzie R - promień krzywizny toru w danym punkcie.

W ruchu prostoliniowym jednostajnie zmiennym (przyspieszonym lub opóźnionym) całkowanie wzoru (1) daje równanie ruchu w postaci ogólnej:

(6)

Całkowanie równania (2) daje zaś wyrażenie określające zależność prędkości od czasu:

(7)

1. Spadek swobodny

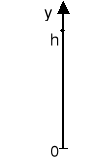
Jeśli ciało spada swobodnie z wysokości h (h << R) na powierzchnię Ziemi, to równanie ruchu w przyjętym jednowymiarowym układzie współrzędnych 0y ma postać:

skąd możemy obliczyć czas spadania

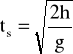
(8)

oraz prędkość w punkcie upadku:

(9)

1.2. Rzut pionowy

Ciało zostaje rzucone pionowo do góry z prędkością początkową v₀. Równanie ruchu w układzie 0y ma postać:

Prędkość ciała zmienia się z upływem czasu zgodnie z wzorem:

Te dwa równania pozwalają obliczyć:

- czas wznoszenia:

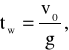
(10)

- wysokość maksymalnego wzniesienia:

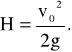
(11)

1.3. Rzut poziomy

Ciału znajdującemu się na wysokości h nadano prędkość poziomą v₀. Układ równań ruchu ciała w układzie współrzędnych pokazanym na rys. 1.3 ma postać:

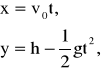
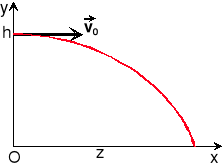
Rys. 1.3. Rzut poziomy

natomiast równanie toru:

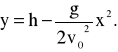
Stąd obliczamy zasięg rzutu poziomego:

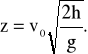
(12)

1.4. Rzut ukośny

Ciało znajdujące się na wysokości h = 0 zostało rzucone z prędkością v₀ skierowaną pod kątem  do poziomu. Układ równań ruchu ciała w układzie współrzędnych pokazanym na rys. 1.4 ma postać:

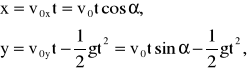
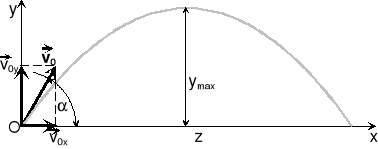
Rys. 1.4. Rzut ukośny

a równanie toru:

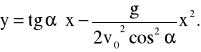
Zasięg rzutu ukośnego:

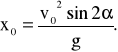
(13)

Wysokość maksymalnego wzniesienia

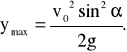
(14)

Czas trwania ruchu:

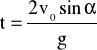
(15)

1.5. Ruch obrotowy

Prędkość kątową definiujemy następująco:

(16)

gdzie  jest kątem zakreślonym przez promień wodzący punktu w czasie dt.

Przyspieszenie kątowe:

(17)

Wielkości te związane są z wielkościami kinematycznymi ruchu postępowego:

(18)

(19)

(20)

W ruchu obrotowym jednostajnie zmiennym (przyspieszonym lub opóźnionym) całkowanie wzoru (16) daje równanie ruchu obrotowego:

(21)

Po scałkowaniu równania (17) otrzymamy wyrażenie określające zależność prędkości kątowej od czasu w ruchu obrotowym jednostajnie zmiennym:

(22)

W ruchu jednostajnym po okręgu wprowadzamy pojęcie prędkości obrotowej:

(23)

gdzie T - okres obiegu.

Na ciało poruszające się z prędkością v w układzie obracającym się z prędkością kątową  działa siła Coriolisa, która nadaje mu przyspieszenie Coriolisa:

(24)

1. Prędkość nurtu rzeki v₁ = 4 m/s, zaś prędkość łodzi względem wody v₂ = 36 km/h. Oblicz średnią prędkość łodzi, która płynęła tam i z powrotem pomiędzy dwoma mostami.

2. Ciało poruszające się ruchem jednostajnie przyspieszonym w ciągu trzeciej sekundy ruchu przebyło drogę 5 m. Jaką drogę przebyło ciało w czasie 4 sekund?

3. Z jakiej wysokości spadło ciało, jeśli w ostatniej sekundzie ruchu przebyło drogę 15 m?

4. Dwie jednakowe kulki wyrzucono do góry kolejno jedna za drugą z taką samą prędkością początkową v₀ = 10 m/s. O ile później wyrzucono drugą kulkę, jeżeli spotkały się one w połowie wysokości maksymalnej?

5. Z samolotu lecącego poziomo z prędkością v = 900 km/h na pułapie h = 300 m puszczono bombę. Oblicz zasięg poziomy, prędkość w punkcie upadku i kąt upadku bomby.

6. Wentylator obraca się wykonując n = 3000 obr/min. Po wyłączeniu prądu wentylator zatrzymuje się po czasie t = 3 min. Ile obrotów wykonają śmigła wentylatora podczas hamowania?

7. Z dwóch miast odległych o L = 100 km wyjeżdżają dwa samochody: jeden z prędkością v₁ = 50 km/h, drugi z prędkością v₂ = 75 km/h, lecz z opóźnieniem t = 10 min. Po jakim czasie i w którym miejscu spotkają się samochody?

8. Oblicz naszą prędkość względem osi Ziemi. Przyjąć: promień Ziemi R = 6400 km, szerokość geograficzna ϕ = 50°.

9. Lokomotywa porusza się z szybkością v₀ = 15 m/s. Na drodze s = 34 m działał hamulec, wskutek czego szybkość zmniejszyła się do v = 5 m/s. Określić czas hamowania i opóźnienie podczas hamowania (przyjmując, że opóźnienie było stałe).

10. Ciało porusza się ruchem jednostajnie przyspieszonym z prędkością początkową v₀ = 2 m/s i w pewnej chwili ma prędkość v₁ = 10 m/s. Oblicz prędkość ciała w połowie przebytej drogi.

11. Czas wjeżdżania windy na wieżę telewizyjną o wysokości h = 340 m wynosi t = 60 s. Pierwszą część drogi winda przebywa ze stałym przyspieszeniem do osiągnięcia prędkości v = 7 m/s, drugą część drogi przebywa ruchem jednostajnym, a trzecią ruchem jednostajnie opóźnionym. Obliczyć przyspieszenie windy przyjmując, że jest ono równe co do wartości bezwzględnej opóźnieniu podczas hamowania.

12. Ciało spadając swobodnie przebywa 1/4 swego ruchu w ostatniej sekundzie ruchu. Z jakiej wysokości ciało spadało?

13. Z wierzchołka urwiska spada kamień. Człowiek, stojący na górze, słyszy odgłos upadku kamienia po czasie t = 7 s. Znaleźć wysokość urwiska, jeśli prędkość dźwięku w powietrzu c = 340 m/s.

14. Z balonu wznoszącego się z prędkością v₀ = 5 m/s puszczono kamień, który upadł po czasie t = 8 s. Na jakiej wysokości znajdzie się balon w momencie upadku kamienia?

15. Uczeń „gapiąc” się w okno zobaczył kamień rzucony do góry, który po 2 s ponownie minął okno podczas spadania. Oblicz prędkość początkową kamienia rzuconego do góry, jeśli okno znajduje się na wysokości h = 5 m.

16. Kulka o promieniu r = 1 cm, tocząca się po płaszczyźnie poziomej z prędkością v = 4 m/s, wpada do pionowej szczeliny o szerokości b = 20 cm i głębokości h = 1 m (rys. 1.20). Ile razy kulka uderzy o ścianki szczeliny? Zderzenia traktujemy jako idealnie sprężyste.

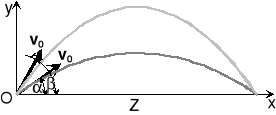
Rys. 1.21. Zadanie 30 (problem stromości toru rzutu ukośnego)

17. Pocisk wystrzelony ukośnie z prędkością v₀ pod kątem α = 35° do poziomu upada w punkcie odległym o Z od miejsca wyrzutu (rys. 1.21). Pod jakim kątem β ≠ α należy wystrzelić pocisk, aby zasięg Z był ten sam?

18. Przy jakim kącie wystrzału zasięg rzutu ukośnego jest maksymalny?

19. Pod jakim kątem do poziomu należy wyrzucić ciało, aby zasięg rzutu był równy jego wysokości maksymalnej?

20. Pojazd gąsienicowy jedzie z prędkością 60 km/h. O ile należy zmniejszyć prędkość jednej z gąsienic, aby pojazd wykonał skręt o promieniu R = 40 m? Szerokość pojazdu b = 3 m. Promień skrętu mierzony jest do środka pojazdu.

21. Pocisk opuszcza lufę karabinu z prędkością v = 600 m/s. Oblicz prędkość obrotową pocisku wiedząc, że w lufie pocisk wykonał jeden obrót. Długość lufy l = 60 cm.

Ruch odbywa się w pobliżu powierzchni Ziemi.

Czas wznoszenia równy jest czasowi spadania.

Przyspieszenie kątowe i prędkość kątowa są wektorami skierowanymi wzdłuż osi obrotu. Zwrot wektora prędkości kątowej określa reguła śruby prawoskrętnej, natomiast zwrot wektora przyspieszenia kątowego zależy od wartości pochodnej d/dt.

36 Kinematyka

Kinematyka 35

PRZYKŁADY

---