PROJEKTOWANIE BADAŃ i METODY ANALIZY STATYSTYCZNEJ I
Wielowymiarowe rozkłady zmiennych losowych cz. I i II
Zad. 1
Gęstość dwuwymiarowej zmiennej losowej ![]()
dana jest wzorem
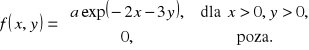
Wyznaczyć stałą a.
Wyznaczyć rozkłady brzegowe.
Sprawdzić, czy zmienne X i Y są niezależne.
Wyznaczyć rozkład warunkowy zmiennej losowej X przy warunku
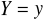
.Obliczyć
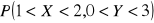
.
Zad. 2
Gęstość dwuwymiarowej zmiennej losowej ![]()
dana jest wzorem
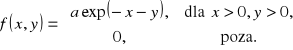
Wyznaczyć stałą a.
Sprawdzić, czy zmienne X i Y są niezależne.
Obliczyć
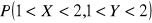
.
Zad. 3*
Gęstość dwuwymiarowej zmiennej losowej ![]()
dana jest wzorem
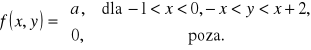
Wyznaczyć stałą a.
Wyznaczyć rozkłady brzegowe.
Zad. 4
Wyznaczyć dystrybuantę dwuwymiarowej zmiennej losowej ![]()
, której gęstość dana jest wzorem
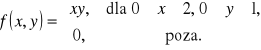
Zad. 5
Gęstość dwuwymiarowej zmiennej losowej ![]()
dana jest wzorem

Wyznaczyć gęstości brzegowe.
Wyznaczyć gęstości warunkowe.
Wyznaczyć wektor wartości oczekiwanych oraz macierz kowariancji.
Zad. 6
Wiedząc, że wektor losowy ![]()
ma rozkład normalny ![]()
, znaleźć rozkład 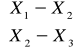
.
Zad. 7
Wiedząc, że wektor losowy ![]()
ma rozkład normalny ![]()
, znaleźć rozkład ![]()
.
Zad. 8
Dany jest wektor losowy ![]()
o rozkładzie normalnym ![]()
, gdzie 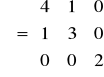
.
Czy zmienne losowe
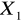
i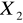
są niezależne?Czy niezależne są
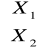
i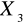
?
Zad. 9
Dany jest wektor losowy ![]()
o rozkładzie normalnym ![]()
z parametrami
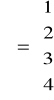
, 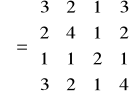
Wyznaczyć rozkład wektora
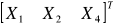
.Wyznaczyć rozkład warunkowy
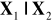
, gdzie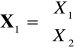
,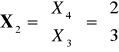
.Wyznaczyć rozkład warunkowy
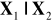
, gdzie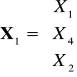
,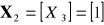
.Wyznaczyć rozkład wektora
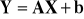
, gdzie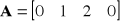
,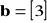
.
Zad. 10
Dany jest wektor losowy ![]()
o rozkładzie normalnym ![]()
z parametrami
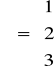
, 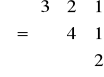
Wyznaczyć rozkład wektora
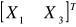
.Wyznaczyć rozkład warunkowy
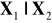
, gdzie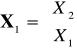
,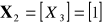
.Wyznaczyć rozkład wektora
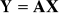
, gdzie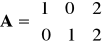
.
Zad. 11
W badaniu miesięcznych wydatków (w zł.) na energię (zmienna ![]()
), telefon (zmienna ![]()
), gaz (zmienna ![]()
) dla próby 30 rodzin otrzymano, że średnie wydatki w złotych wynoszą odpowiednio
![]()
, ![]()
, ![]()
,
macierz kowariancji
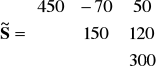
Wiedząc, że rozkład wektora losowego ![]()
jest normalny, czy można przypuszczać, że te wydatki wynoszą średnio ![]()
? Przyjąć poziom istotności ![]()
.
Zad. 12
Zbadano pot 20 kobiet pod względem trzech składowych: ![]()
- wskaźnik potu, ![]()
- zawartość sodu, ![]()
- zawartość potasu. Otrzymano następujące wyniki:
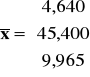
, 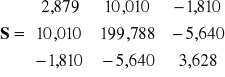
.
Wiedząc, że rozkład wektora losowego ![]()
jest normalny ![]()
, zweryfikować hipotezę ![]()
wobec ![]()
? Przyjąć poziom istotności ![]()
.
Zad. 13
Zbadano losowo wybranych 30 studentów matematyki i 20 studentów fizyki pod względem ocen z języka angielskiego (zmienna ![]()
) i niemieckiego (zmienna ![]()
). Otrzymano następujące wyniki:
Studenci matematyki:
![]()
, ![]()
, 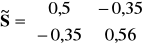
.
Studenci fizyki:
![]()
, ![]()
, 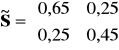
.
Zakładając normalność wektora losowego ![]()
sprawdzić, czy średnie ocen uzyskanych
przez studentów obu kierunków są takie same. Przyjąć poziom istotności ![]()
.
Zad. 14
W badaniu struktury miesięcznych wydatków studentów i studentów uwzględniono wydatki na żywność (zmienna ![]()
), wydatki na książki (zmienna ![]()
) i wydatki na ubrania (zmienna ![]()
). Dla losowo wybranych 30 studentek i 20 studentów otrzymano następujące średnie
w zł.:
Studentki:
![]()
, ![]()
, ![]()
,
Studenci:
![]()
, ![]()
, ![]()
.
Odwrotność uśrednionej macierzy kowariancji dla tej próby wyniosła:
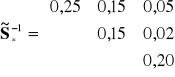
.
Wiedząc, że rozkład wektora losowego ![]()
jest normalny, czy można stwierdzić, że struktury wydatków studentek i studentów są takie same.
Zad. 15
Zweryfikować hipotezę, czy macierz wariancji - kowariancji w populacji generalnej
o dwuwymiarowym rozkładzie normalnym ![]()
jest równa 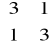
, jeśli dla 100 elementowej próby pobranej z tej populacji obciążona macierz wariancji - kowariancji
ma postać 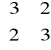
. Przyjąć poziom istotności ![]()
.
Zad. 16*
Zbadano losowo wybranych 20 studentów ze względu na wzrost (zmienna ![]()
) i wagę (zmienna ![]()
), otrzymano odpowiednio następujące wyniki:
172 89
160 54
166 83
158 71
187 82
160 83
163 108
177 82
153 85
159 85
169 75
168 80
171 97
188 85
171 69
174 79
168 77
177 85
183 78
172 82
Wiedząc, że rozkład wektora losowego ![]()
jest normalny, czy można przypuszczać, że te średnie wynoszą odpowiednio ![]()
? Przyjąć poziom istotności ![]()
.
Zad. 17*
Zbadano losowo wybranych pracowników z wykształceniem wyższym, z dwóch firm F1 i F2 (15 pracowników z pierwszej firmy i 10 z drugiej), pod względem wynagrodzenia (zmienna ![]()
), średniej ocen na świadectwie maturalnym (zmienna ![]()
) oraz średniej ocen na studiach (zmienna ![]()
). Otrzymano następujące wyniki odpowiednio dla firmy F1 i firmy F2:
1531.09 3.20 3.35 5664.44 3.39 4.89
2726.67 3.53 4.38 4601.96 5.15 4.16
5228.50 3.75 3.85 4927.52 3.94 5.00
1763.96 3.98 5.00 4350.83 3.71 3.31
3502.66 4.92 5.00 2600.26 3.42 4.68
2706.50 3.31 4.10 4710.56 3.03 3.94
5525.26 3.68 3.83 3197.18 4.93 4.66
5920.71 3.88 5 .00 4412.57 4.17 4.31
3604.19 4.82 4.39 4324.51 3.61 4.27
5942.44 3.74 4.23 2708.78 4.57 5.00
5481.81 4.48 5.00
2499.85 3.18 4.38
3275.49 4.48 4.37
3724.04 4.04 5.00
3818.33 4.99 3.63
Wiedząc, że rozkład wektora losowego ![]()
jest normalny, zweryfikować hipotezę zerową o równości rozważanych wektorów wartości oczekiwanych w obu populacjach. Przyjąć poziom istotności ![]()
.
5
Wyszukiwarka
Podobne podstrony:
Cw24 25IV, PBiMAS, Frątczak, PBIMAS, PBiMAS cw123, PBiMAS cw123, Materiały do ćwiczeń PBiMASI-cz.I.I
ESTYMACJA I WERYFIKACJA - wzory - repetytorium, PBiMAS, Frątczak, PBIMAS, PBiMAS cw123, PBiMAS cw123
Cw17 18IV, PBiMAS, Frątczak, PBIMAS, PBiMAS cw123, PBiMAS cw123, Materiały do ćwiczeń PBiMASI-cz.I.I
opis zbiorow, PBiMAS, Frątczak, PBIMAS, PBiMAS cw123, PBiMAS cw123, Materiały do ćwiczeń PBiMASI-cz.
Zadania na estymację i weryfikację hipotez - repetytorium, PBiMAS, Frątczak, PBIMAS, PBiMAS cw123, P
nissan almera 15 16v
akumulator do renault scenic gand ii jm01 20 16v 15 dci 19 dc
akumulator do mazda 323 s v ba 13 16v 15 16v
akumulator do kia rio kombi 13 15 16v
akumulator do daihatsu gran move g3 15 16v 16 16v
akumulator do mitsubishi lancer vii ckpa 13 12v gl glx 15 16v
akumulator do nissan almera hatchback ii n16 15 16v 18 16v 15
akumulator do suzuki sx4 hatchabck 15 i 16v 16 i 16v vvt 2w
akumulator do mazda demino a6 a7 12 13 16v 13 14 15 15 16v
akumulator do mitsubishi lancer vii coupe ckpa 15 16v 18 18 g
akumulator do mitsubishi lancer vii estate ckpa 15 16v 18 20
akumulator do mitsubishi lancer ix saloon 15 i 16v 15 18
akumulator do honda civic vi fastback mb 14 16v 15 16v 16 16v
akumulator do vaz 2110 2110 m 13 15 15 16v
więcej podobnych podstron