Wyznaczanie współczynnika lepkości cieczy

1. Cel ćwiczenia

Celem ćwiczenia jest wyznaczenie współczynnika lepkości gliceryny oraz oleju silnikowego w oparciu o opadanie metalowych kulek o różnych średnicach w badanej cieczy.

2. Opis teoretyczny

Lepkość jest jedną z najważniejszych cech płynów. Charakteryzuje opór płynów wewnętrznych przeciw płynięciu. Wskutek tarcia występującego między cząsteczkami cieczy, poruszająca się cząsteczka pociąga za sobą sąsiadujące cząsteczki tym silniej, im większa jest siła lepkości. Te cząsteczki pociągają następne itd. … Każda następna warstwa porusza się jednak nieco wolniej, tym wolniej, im mniejsza lepkość cieczy. Prędkość spada do zera dla cząstek przy ściankach, które są jakby „przyklejone”, a więc nieruchome. Tak więc maksymalną prędkość mają cząsteczki na osi rury. W sytuacji, gdy prędkość przepływu cieczy przez gładką rurę jest mała mamy do czynienia z przepływem laminarnym, czyli warstwowym. Kolejne warstwy cieczy płyną nie zakłócając się wzajemnie. Prędkość cząstek przepływających przez dany punkt jest zawsze taka sama. Przy dużych prędkościach w cieczy pojawiają się zawirowania i ruch z laminarnego zmienia się w turbulentny.

Przepływ cieczy wokół dowolnego ciała zależ od gęstości cieczy ρ i współczynnika lepkości ɳ, charakterystycznego wymiaru liniowego l oraz prędkości przepływu v. Interesujące jest to, że charakter przepływu nie zależy bezpośrednio od tych parametrów, lecz zależy od bezwymiarowej kombinacji tych wielkości. Ich bezwymiarową kombinacją jest:

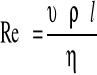
, czyli wielkość zwana liczbą Reynoldsa.

Dla małych liczb Reynoldsa, Re<<1, decydującą rolę w sile oporu odgrywa lepkość-przepływ cieczy nazywamy „laminarnym” - bezwymiarowym.

Dla przepływu laminarnego Stokes wprowadził wzór na siłę oporu działającą na kulkę opadającą pod wpływem siły ciężkości w cieczy wypełniającej całą przestrzeń. Przypadki cieczy opływającej ciało i ciała przemieszczającego się w cieczy są sobie równoważne. Siłę oporu działającą na kulkę w warunkach opisanych przez Stokesa można przedstawić następująco:

F=-6π·ɳ·l·ν

3. Wykonanie ćwiczenia:

Układ pomiarowy:

Podczas wykonywania ćwiczenia do dyspozycji mieliśmy:

-śrubę mikrometryczną o dokładności 0,01mm

-wagę laboratoryjną o błędzie stałym 0,1mg i dokładności 0,1mg

-stoper o dokładności 0,01s

-rury z cieczami: gliceryną i olejem silnikowym,

Dane:

Ciężar właściwy cieczy

• gliceryna 1,473 g/cm³ = 1473 kg/m³;

• olej silnikowy 0,867 g/cm³ = 867 kg/m³;

Średnice wewnętrzne cylindrów:

• z gliceryną ∅₁= 27,9 mm;

• z olejem silnikowym ∅₂= 28,1 mm.

4. Wykonanie ćwiczenia: Wyniki i analiza błędów:

Przed rozpoczęciem pomiarów ruchu kulek w cylindrach określałyśmy:

• Średnice kulek;

• Masę kulek.

Przy pomocy śruby mikrometrycznej dokonałyśmy pomiarów średnic dla trzech kulek o różnych wielkościach. Poniższa tabelka przedstawia otrzymane wyniki:

l.p.	mała kulka [mm]	średnia kulka [mm]	duża kulka [mm]
1.	2,99	3,49	3,99
2.	2,97	3,48	3,98
3.	2,98	3,48	3,99
4.	2,98	3,49	4,00
5.	2,97	3,49	4,00
6.	2,98	3,49	3,99
7.	2,98	3,50	3,99
8.	2,98	3,49	4,00
9.	2,97	3,49	4,00
10.	2,98	3,49	4,00
11.	2,97	3,50	3,99
12.	2,97	3,50	3,99
13.	2,98	3,49	3,99
14.	2,98	3,49	3,99
15.	2,97	3,49	3,98
16.	2,97	3,50	3,98
17.	2,97	3,49	3,99
18.	2,98	3,49	3,99
19.	2,98	3,48	4,00
20.	2,98	3,49	3,99
21.	2,97	3,49	4,00
22.	2,97	3,49	4,00
23.	2,96	3,49	4,00
24.	2,97	3,49	4,00
25.	2,97	3,49	3,99
26.	2,98	3,49	3,98
27.	2,97	3,49	3,99
28.	2,98	3,48	3,99
29.	2,97	3,49	4,00
30.	2,97	3,49	3,98

Średnie śednice kulek:

Małej-(2,97
0,01) [mm]

Średniej-(3,49
0,01) [mm]

Dużej-(3,99
0,01) [mm]

Przy użyciu wagi laboratoryjnej zważyliśmy kulki. Ze względu na wielkość i kształt ważonych przedmiotów umieściliśmy je w papierku, który uprzednio zważyliśmy. Wyniki pomiarów:

masa papierka-(225,3
0,1)[mg]

masa małej kulki-(67,8
0,1)[mg]

masa średniej kulki-(110,2
0,1)[mg]

masa dużej kulki-(176,5
0,1)[mg]

Przy pomocy stopera zmierzyłyśmy czas opadania kulek wkładanych do rur z cieczą. Pomiarów dokonałyśmy dla oleju silnikowego i gliceryny. Czas opadania obarczony jest błędem wynikłym z czasu reakcji i uruchamiania stopera. Zakładamy jednak że we wszystkich przypadkach czas ten był sobie równy (pomiarów czasu dokonywała jedna osoba we wszystkich przypadkach).

Na początku eksperymentalnie wyznaczyłyśmy odcinek (l) pomiarowy w którym kulka porusza się ruchem jednostajnym.

Pomiary dla oleju silnikowego:

l.p	czas małej kulki [s] dla l=80cm	czas średniej kulki [s] dla l=100cm	czas dużej kulki [s] dla l=70cm
1.	6,85	5,82	3,60
2.	6,87	5,90	3,56
3.	6,85	5,83	3,60
4.	6,88	5,81	3,60
5.	6,81	5,83	3,62
6.	6,85	5,82	3,62
7.	6,81	5,78	3,60
8.	6,83	5,81	3,62
9.	6,80	5,94	3,65
10.	6,87	5,83	3,53
11.	6,85	5,81	3,62
12.	6,79	5,90	3,60
13.	6,81	5,84	3,63
14.	6,85	5,82	3,60
15.	6,87	5,93	3,62
16.	6,89	5,81	3,50
17.	6,85	5,82	3,66
18.	6,87	5,79	3,56
19.	6,83	5,83	3,53
20.	6,86	5,81	3,63
21.	6,79	5,90	3,60
22.	6,85	5,84	3,62
23.	6,80	5,81	3,54
24.	6,78	5,79	3,62
25.	6,83	5,82	3,63
26.	6,75	5,84	3,60
27.	6,81	5,83	3,62
28.	6,85	5,81	3,54
29.	6,80	5,82	3,62
30.	6,84	5,84	3,60
średnia	6,84 0,01	5,83 0,01	3,60 0,01

Pomiary dla gliceryny:

l.p	czas małej kulki [s] dla l=80cm	czas średniej kulki [s] dla l=90cm	czas dużej kulki [s] dla l=90cm
1.	25,02	20,59	15,54
2.	25,00	20,60	15,62
3.	25,02	20,66	15,60
4.	25,01	20,69	15,59
5.	25,05	20,60	15,62
6.	25,08	20,65	15,61
7.	25,04	20,69	15,65
8.	25,02	20,61	15,62
9.	25,02	20,66	15,60
10.	25,01	20,64	15,64
11.	25,04	20,61	15,68
12.	25,04	20,67	15,65
13.	25,01	20,60	15,60
14.	25,01	20,65	15,62
15.	25,02	20,59	15,58
16.	25,08	20,62	15,65
17.	25,07	20,66	15,67
18.	25,07	20,61	15,61
19.	25,06	20,64	15,59
20.	25,04	20,60	15,64
21.	-	20,65	-
22.	-	20,62	-
23.	-	20,64	-
24.	-	20,61	-
25.	-	20,60	-
26.	-	20,64	-
27.	-	20,61	-
28.	-	20,66	-
29.	-	20,64	-
30.	-	20,59	-
średnia	25,04 0,01	20,63 0,01	15,62 0,01

Do wyznaczenia współczynnika lepkości potrzeba nam była średnia prędkość graniczna, którą obliczyliśmy, w następujący sposób:

Błąd wyznaczenia prędkości granicznej wyznaczamy metodą różniczki zupełnej:

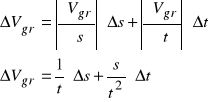
Prędkości graniczne (V_gr):

Olej silnikowy: Gliceryna:

Kulka mała- (0,117
0,004)[m/s] (0,0319
0,0004)[m/s]

Kulka średnia- (0,171
0,006)[m/s] (0,0436
0,0007)[m/s]

Kulka duża- (0,195
0,007)[m/s] (0,0576
0,0011)[m/s]

Z poniższego wzoru obliczyłyśmy lepkość:

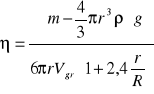
Dla oleju silnikowego:

Kulka mała ɳ=(0,18
0,02)[Pa·s]

Kulka średnia ɳ=(0,15
0,01) [Pa·s]

Kulka duża ɳ=(0,18
0,02) [Pa·s]

Dla gliceryny:

Kulka mała ɳ=(0,59
0,04) [Pa·s]

Kulka średnia ɳ=(0,58
0,03) [Pa·s]

Kulka duża ɳ=(0,59
0,04)[Pa·s]

Błąd obliczyłyśmy z metody różniczki zupełnej:

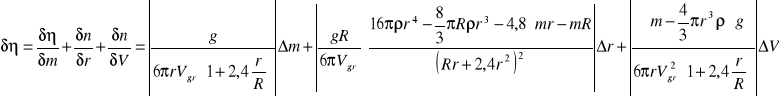
Policzyłyśmy średnią lepkość z trzech pomiarów, ostatecznie otrzymałyśmy:

Dla oleju: ɳ=(0,17
0,02) [Pa·s]

Dla gliceryny: ɳ=(0,59
0,04) [Pa·s]

5. Wnioski:

Podczas badania należało zmierzyć średnic kulek, ich masę oraz czas opadania kulki w danej cieczy (olej silnikowy oraz gliceryna). Na podstawie przeprowadzonych pomiarów oraz danych układu pomiarowego możliwe jest obliczenie prędkości granicznej oraz współczynnika lepkości dla gliceryny i oleju silnikowego.

Wyniki pomiarów nie są idealnie zgodne z zestawieniami w tablicach fizycznych, (zaczerpnięta z tablic wartość lepkości gliceryny wynosi: 1,480[Pa·s] w 20° C, oraz
0,6 [Pa·s] w temperaturze 30° C ), co może być spowodowane tym, że kulki nie zawsze poruszały się dokładnie po osi symetrii rurki. Dodatkowa rozbieżność wyników jest zależna od dokładności pomiaru czasu opadania kulki w poszczególnej cieczy oraz od temperatury otoczenia, w którym odbywały się pomiary. Ponieważ nie znamy rodzaju oleju nie jesteśmy w stanie sprawdzić jaka jest jego lepkość.

---