POLITECHNIKA RADOMSKA Wydz. Transportu Kier. elektrotechnika
|
LABORATORIUM TEORII STEROWANIA |
Data: 09.03.1999.
|
||||
Imię i nazwisko: |
Szkudlarek Karol Kurek Wiesław Pawłowski Sławomir |
Grupa: 25A
|
Zespół: 2
|
Rok akademicki: 1998 / 99
|
||
Nr ćwiczenia: 1
|
Temat: Charakterystyki liniowych członów układów regulacji automatycznej
|
Ocena:
|
||||
1 PRZEBIEG ĆWICZENIA:
Człon inercyjny zrealizowany na elementach RC
f [kHz]
|
A |
B |
C |
m=B/A |
L=20 log M. |
ρ=asin C/B cccC/B
|
ω [rad/s] |
1 0,350 |
3,4 |
2,60 |
0,40 |
0,76 |
-2,38 |
-8,62 |
2198 |
2,2 0,790 |
3,4 |
2,40 |
060 |
0,70 |
-3,09 |
-14,47 |
4961 |
3,15 2,050 |
3,2 |
2,10 |
1,04 |
0,65 |
-3,74 |
-29,34 |
12874 |
4,4 3,150 |
3,2 |
1,80 |
1,20 |
0,56 |
-5,03 |
-41,29 |
19782 |
5,7 4,850 |
3,0 |
1,40 |
1,00 |
0,46 |
-7,74 |
-45,23 |
30458 |
6,6 5,150 |
3,0 |
1,20 |
1,00 |
0,40 |
-8,95 |
-46,09 56,09 |
32342 |
7,2 6,050 |
3,0 |
1,20 |
0,90 |
0,40 |
-9,95 |
-48,59 |
37994 |
7,9 7,330 |
3,0 |
0,86 |
0,80 |
0,28 |
-11,05 |
-68,43 |
46032 |
8,6 8,120 |
3,0 |
0,80 |
0,76 |
0,27 |
-12,37 |
-71,80 |
50993 |
9,4 9,150 |
2,9 |
0,70 |
0,67 |
0,26 |
-13,70 |
-75,18 |
57187 |
10,8 |
3,0 |
0,65 |
0,64 |
0,23 |
-15,76 |
-79,23 |
67824 |
12,8 |
3,0 |
0,60 |
0,59 |
0,20 |
-17,97 |
-80,88 |
80478 |
20,6 |
3,0 |
0,40 |
0,39 |
0,13 |
-18,72 |
-81,15 |
129993 |
|
|
|
|
|
|
|
|
RC + U2(t) = U1(t) G(s) = = gdzie T= RC, k = 1
R=474 [Ω] ; C=0.1011 [μF]
T=474*(0.1011*10-6)=47*10-6 ; k=1
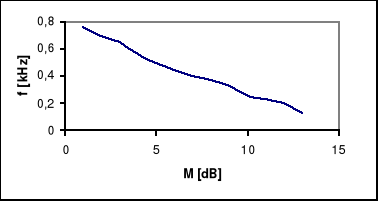
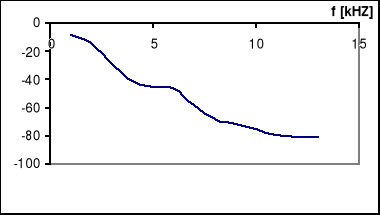
Człon oscylacyjny zrealizowany na elementach RLC
LC + RC + U2 = U1
G(s) = przy czym: ωo2 = ; ξ= ; k = 1
R=430 [Ω] ; L=31 [mH] ; C=0.0066 [μF]
ωo2 = =48*1010 ⇒ ωo=69911.26 [Rad/s]
ξ==0.003 ; k=1
f [kHz] |
C |
A |
B |
M.=B/A |
L=20 log M |
ρ=asin(C/B) |
ω [rad/s]
|
0 |
0 |
0 |
0 |
- |
0 |
0 |
0 |
6,00 |
3,3 |
3,00 |
0,50 |
0,91 |
-1,11 |
9,59 |
37680 |
7,30 |
3,3 |
3,20 |
0,60 |
0,96 |
-0,35 |
10,81 |
45844 |
9,20 |
3,24 |
3,60 |
0,76 |
1,11 |
0,90 |
12,18 |
57776 |
11,00 |
3,2 |
4,20 |
1,20 |
1,31 |
2,34 |
16,6 |
69080 |
12,82 |
3,2 |
5,20 |
2,20 |
1,62 |
4,19 |
25,02 |
80509 895456 |
15,20 |
3,0 |
7,20 |
5,80 |
2,60 |
8,29 |
53,66 |
95456 |
16,30 |
2,8 |
7,60 |
7,40 |
2,71 |
8,65 |
76,82 |
102364 |
17,80 |
2,8 |
6,80 |
6,30 |
2,42 |
7,67 |
11372 |
111784 |
19,40 |
3,0 |
5,00 |
3,60 |
1,67 |
4,45 |
134,42 |
121832 |
21,70 |
3,2 |
3,00 |
1,70 |
0,93 |
-0,63 |
146,52 |
136272 |
22,90 |
3,2 |
2,60 |
1,10 |
0,81 |
-1,83 |
156,58 |
143812 |
24,25 |
3,2 |
2,20 |
0,80 |
0,68 |
-3,34 |
149,32 |
152290 |
26,60 |
3,2 |
1,60 |
0,50 |
0,50 |
-6,02 |
161,8 |
163280 |
28,90 |
3,2 |
1,20 |
0,37 |
0,37 |
-8,63 |
165,3 |
181492 |
30,80 |
3,2 |
1,00 |
0,30 |
0,31 |
-10,17 |
167,35 |
193424 |
31,70 |
3,2 |
0,84 |
0,20 |
0,26 |
-11,70 |
168,09 |
199076 |
2 WZORY I OBLICZENIA:
M=
M==0.88 M==2.42
M==0.96 M==1.67
M==1.11 M==0.93
M==1.31 M==0.81
M==1.62 M==0.68
M==2.6 M==0.0.5
M==2.71 M==0.37
M==0.31 M==0.26
L=20 log M
L=20 log 0.88 = -1.11 L=20 log 1.67 = 4.45
L=20 log 0.96 = -0.35 L=20 log 0.93 = -0.63
L=20 log 1.11 = 0.90 L=20 log 0.81 = -1.83
L=20 log 1.31 = 2.34 L=20 log 0.68 = -3.34
L=20 log 1.62 = 4.19 L=20 log 0.50 = -6.02
L=20 log 2.60 = 8.29 L=20 log 0.37 = -8.63
L=20 log 2.71 = 8.65 L=20 log 0.31 = -10.17
L=20 log 2.42 = 7.67 L=20 log 0.26 = -11.7
ϕ= arc sin
ϕ= arc sin = 9.59 ϕ= arc sin = 46.05
ϕ= arc sin = 8.98 ϕ= arc sin = 34.51
ϕ= arc sin = 12.18 ϕ= arc sin = 25.02
ϕ= arc sin = 16.6 ϕ= arc sin = 21.32
ϕ= arc sin = 25.02 ϕ= arc sin = 18.2
ϕ= arc sin = 53.66 ϕ= arc sin = 19.47
ϕ= arc sin = 76.82 ϕ= arc sin = 17.45
ϕ= arc sin = 67.89 ϕ= arc sin = 13.77
Uwagi i wnioski :
W przypadku członu inercyjnego otrzymane wyniki zarówno metodą analityczną jak i na podstawie wykresu pokrywają
się ze sobą różnice są niewielkie i wynikają głównie z niedokładności wykresu. Natomiast w przypadku członu oscylacyjnego ω0 otrzymana z obliczeń wynosi 69900 natomiast z wykresu odczytujemy 80000. Jest najprawdopodobniej winą błędnej wartości jednego z elementów RLC.
Po przeprowadzeniu ćwiczenia możemy stwierdzić, że odpowiedzi układów są zgodne z wykresami
teoretycznymi. Oczywiście są pewne różnice, ale jest to spowodowane niedokładnością odczytu z
oscyloskopu. Wyliczone parametry układów są podobne do wyznaczonych na podstawie wykresów odpowiedzi
układów.
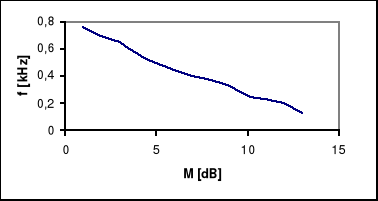
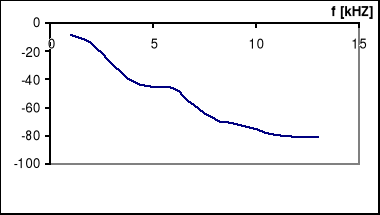
Wyszukiwarka
Podobne podstrony:
Ch-ki czestotliwość, Elektrotechnika, SEM4, ARA ćwiczenia
Korekcja liniowych układów regulacji, Elektrotechnika, SEM4, ARA ćwiczenia
sprawko 9 elektronika sem4, Sprawozdanie z przeprowadzonego ćwiczenia nr 9 -
sprawko 9 elektronika sem4, Sprawozdanie z przeprowadzonego ćwiczenia nr 9 -
CWICZENIE 3 ch ki czasowe RLC PW
Cwiczenia opis, Elektrotechnika, SEM4, Teoria Pola Krawczyk
HA ja na ARA cwiczenia 2010
Obwody magnetycznie sprzężone p, Elektrotechnika, SEM4, Teoria Pola Krawczyk
ARA cwiczenia 1
Badanie transformatora 1 fazowego p, Elektrotechnika, SEM4, Teoria Pola Krawczyk, wnioski
Cw2 mostek thomsona, Elektrotechnika, SEM4, Metrologia Krawczyk
FERRO1, Elektrotechnika, SEM4, Teoria Pola Krawczyk, wnioski
Cw1 pom mocy, Elektrotechnika, SEM4, Metrologia Krawczyk
Elektronika - gotowe, Wykaz ćwiczeń w Pracowni Elektroniki oraz źródła opisu ćwicz, Wykaz ćwiczeń w
Ch ki czasowe
09'', Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, sprawozdania, Sprawozdania, Lab
Metrologia sem 2 Tr El EiT 1, Elektrotechnika, SEM4, Metrologia Krawczyk
05', Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, sprawozdania, Sprawozdania, Labo
więcej podobnych podstron