Politechnika Warszawska
Wydział
Samochodów i Maszyn Roboczych
Praca Domowa
Podstawy eksploatacji i niezawodności
Michał Kaczmarczyk gr. 2.4
Nr zbioru 24 :
Nr. przedziału |
Granice przedziału |
Środek przedziału |
Liczba obserwacji |
|
|
|
|
|
L |
XLj |
XPj |
Xj |
nj |
Xj*nj |
((Xj)^2)nj |
∑nj |
N-∑nj |
1 |
0 |
56 |
28 |
1 |
28 |
784 |
1 |
749 |
2 |
56 |
112 |
84 |
1 |
84 |
7056 |
2 |
748 |
3 |
112 |
168 |
140 |
6 |
840 |
117600 |
8 |
742 |
4 |
168 |
224 |
196 |
36 |
7056 |
1382976 |
44 |
706 |
5 |
224 |
280 |
252 |
112 |
28224 |
7112448 |
156 |
594 |
6 |
280 |
336 |
308 |
201 |
61908 |
19067664 |
357 |
393 |
7 |
336 |
392 |
364 |
211 |
76804 |
27956656 |
568 |
182 |
8 |
392 |
448 |
420 |
127 |
53340 |
22402800 |
695 |
55 |
9 |
448 |
504 |
476 |
45 |
21420 |
10195920 |
740 |
10 |
10 |
504 |
560 |
532 |
9 |
4788 |
2547216 |
749 |
1 |
11 |
560 |
616 |
588 |
1 |
588 |
345744 |
750 |
0 |
|
|
|
Suma |
750 |
255080 |
91136864 |
|
|
Obliczam wartości:
Wariancja:
σ2 = 5843,3
Wartość średnia:
![]()
= 340,1
Odchylenie standardowe:
σ = 76,4
Liczność próbki:
N = 750
Podstawowe miary niezawodności:
- środek przedziału
- liczba obserwacji
- funkcja gęstości
- funkcja zawodności (dystrybuanta)
- funkcja niezawodności
- funkcja ryzyka
Nr. Przedziału |
Środek przedziału |
Liczba obserwacji |
Funkcja gęstości |
Funkcja zawodności (dystrybułanta) |
Funkcja niezawodności |
Funkcja ryzyka |
j |
Xj |
nj |
f(x)=nj/(N*Dx) *10-3 |
F(x)=Snj/N |
R(x)=(N-Snj)/N |
l(x)=nj/Dx(N-Snj)*103 |
1 |
28 |
1 |
0,024 |
0,001 |
0,999 |
0,024 |
2 |
84 |
1 |
0,024 |
0,003 |
0,997 |
0,024 |
3 |
140 |
6 |
0,143 |
0,011 |
0,989 |
0,144 |
4 |
196 |
36 |
0,857 |
0,059 |
0,941 |
0,911 |
5 |
252 |
112 |
2,667 |
0,208 |
0,792 |
3,367 |
6 |
308 |
201 |
4,786 |
0,476 |
0,524 |
9,133 |
7 |
364 |
211 |
5,024 |
0,757 |
0,243 |
20,703 |
8 |
420 |
127 |
3,024 |
0,927 |
0,073 |
41,234 |
9 |
476 |
45 |
1,071 |
0,987 |
0,013 |
80,357 |
10 |
532 |
9 |
0,214 |
0,999 |
0,001 |
160,714 |
11 |
588 |
1 |
0,024 |
1,000 |
0,000 |
- |
Poniżej zamieszczam wartości uzyskane z przeprowadzonego rozkładu normalnego:
Test zgodności χ 2 :
- Liczba stopni swobody
r = 8
- Poziom istotności
α = 0,05
Otrzymane wyniki:
- wartość krytyczna rozkładu
χ2 = 15,507
- wartość dla zadanego rozkładu
χ2 = 1,480
Hipoteza może zostać przyjęta ponieważ wartość dla rozkładu jest mniejsza od wartości krytycznej.
Rozkład normalny:
Liczba obserwacji |
Standaryzacja |
Funkcja gęstości |
Dystrybułanta |
Funkcja niezawodności |
Funkcja ryzyka |
Standaryzacja na kończch przedziału |
Dystrybułanta na końcach przedziałów |
Prawdop. Zmn. Losowej w przedziale |
Statystyka hi^2 Pearsona |
||||
nj |
uj=(xj-xsr)/s |
f(xj) *10-3 |
F(xj)=F(uj) |
R(xj)=1-F(xj) |
l(xj) *10^3 |
uLj |
|
upj |
F(xLj) |
|
F(xPj) |
|
|
1 |
-3,480 |
0,0024 |
0,0003 |
0,9997 |
0,002 |
-3,80 |
--- |
-3,16 |
0,000 |
-- |
0,001 |
0,0007 |
0,796 |
2 |
-2,847 |
0,0176 |
0,0022 |
0,9978 |
0,018 |
-3,16 |
--- |
-2,53 |
0,001 |
-- |
0,006 |
0,0049 |
0,298 |
13 |
-2,213 |
0,0873 |
0,0134 |
0,9866 |
0,089 |
-2,53 |
--- |
-1,90 |
0,006 |
-- |
0,029 |
0,0233 |
0,053 |
44 |
-1,580 |
0,2904 |
0,0571 |
0,9429 |
0,308 |
-1,90 |
--- |
-1,26 |
0,029 |
-- |
0,103 |
0,0744 |
0,002 |
96 |
-0,946 |
0,6462 |
0,1721 |
0,8279 |
0,781 |
-1,26 |
--- |
-0,63 |
0,103 |
-- |
0,265 |
0,1613 |
0,000 |
142 |
-0,313 |
0,9628 |
0,3773 |
0,6227 |
1,546 |
-0,63 |
--- |
0,00 |
0,265 |
-- |
0,502 |
0,2371 |
0,003 |
142 |
0,321 |
0,9602 |
0,6259 |
0,3741 |
2,567 |
0,00 |
--- |
0,64 |
0,502 |
-- |
0,738 |
0,2365 |
0,008 |
97 |
0,955 |
0,6410 |
0,8301 |
0,1699 |
3,773 |
0,64 |
--- |
1,27 |
0,738 |
-- |
0,898 |
0,1600 |
0,028 |
44 |
1,588 |
0,2865 |
0,9439 |
0,0561 |
5,103 |
1,27 |
--- |
1,90 |
0,898 |
-- |
0,972 |
0,0734 |
0,001 |
13 |
2,222 |
0,0857 |
0,9868 |
0,0132 |
6,515 |
1,90 |
--- |
2,54 |
0,972 |
-- |
0,994 |
0,0228 |
0,027 |
2 |
2,855 |
0,0172 |
0,9978 |
0,0022 |
7,979 |
2,54 |
--- |
3,17 |
0,994 |
-- |
0,999 |
0,0048 |
0,263 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
596 |
|
|
|
|
|
|
|
|
|
|
|
0,9992 |
1,480 |
Rozkład Weibulla dla Xo= -16,36
Nr. przedziału |
Granice przedziału |
Środek przedziału |
Liczba obserwacji |
Korekcja |
Funkcja gęstości |
Dystrybułanta |
Funkcja niezawodności |
Funkcja ryzyka |
Dystrybułanta na końcach przedziałów |
Prawdop. Zmn. Losowej w przedziale |
Statystyka hi^2 Pearsona |
||||
|
XLj |
--- |
XPj |
Xj |
nj |
(Xj-Xo) |
f(xj) *10-3 |
F(xj)=F(uj) |
R(xj)=1-F(xj) |
l(xj) *10^3 |
F(xLj) |
|
F(xPj) |
pj=F(xPj)-F(xLj) |
|
1 |
0 |
--- |
56 |
28 |
1 |
44,4 |
0,0074 |
0,00005 |
1,000 |
0,01 |
0,00 |
-- |
0,00 |
0,0008 |
0,3 |
2 |
56 |
--- |
112 |
84 |
1 |
100,4 |
0,1576 |
0,0035 |
0,996 |
0,16 |
0,00 |
-- |
0,01 |
0,0096 |
5,4 |
3 |
112 |
--- |
168 |
140 |
6 |
156,4 |
0,6416 |
0,0240 |
0,976 |
0,66 |
0,01 |
-- |
0,05 |
0,0369 |
17,0 |
4 |
168 |
--- |
224 |
196 |
36 |
212,4 |
1,5402 |
0,0832 |
0,917 |
1,68 |
0,05 |
-- |
0,13 |
0,0869 |
13,1 |
5 |
224 |
--- |
280 |
252 |
112 |
268,4 |
2,7033 |
0,2017 |
0,798 |
3,39 |
0,13 |
-- |
0,29 |
0,1509 |
0,0 |
6 |
280 |
--- |
336 |
308 |
201 |
324,4 |
3,6604 |
0,3823 |
0,618 |
5,93 |
0,29 |
-- |
0,49 |
0,2030 |
15,6 |
7 |
336 |
--- |
392 |
364 |
211 |
380,4 |
3,8115 |
0,5963 |
0,404 |
9,44 |
0,49 |
-- |
0,70 |
0,2110 |
17,6 |
8 |
392 |
--- |
448 |
420 |
127 |
436,4 |
2,9571 |
0,7899 |
0,210 |
14,07 |
0,70 |
-- |
0,86 |
0,1644 |
0,1 |
9 |
448 |
--- |
504 |
476 |
45 |
492,4 |
1,6269 |
0,9185 |
0,082 |
19,95 |
0,86 |
-- |
0,96 |
0,0919 |
8,3 |
10 |
504 |
--- |
560 |
532 |
9 |
548,4 |
0,5964 |
0,9781 |
0,022 |
27,21 |
0,96 |
-- |
0,99 |
0,0348 |
11,2 |
11 |
560 |
--- |
616 |
588 |
1 |
604,4 |
0,1354 |
0,9962 |
0,004 |
35,97 |
0,99 |
-- |
1,00 |
0,0084 |
4,4 |
|
|
|
|
Suma |
750 |
|
|
|
|
|
|
|
|
0,9987 |
93,06 |
Rozkład Weibulla dla Xo=0
Nr. przedziału |
Granice przedziału |
Środek przedziału |
Liczba obserwacji |
Funkcja gęstości |
Dystrybułanta |
Funkcja niezawodności |
Funkcja ryzyka |
Dystrybułanta na końcach przedziałów |
Prawdop. Zmn. Losowej w przedziale |
Statystyka hi^2 Pearsona |
||||
L |
XLj |
--- |
XPj |
Xj |
nj |
f(xj) *10-3 |
F(xj)=F(uj) |
R(xj)=1-F(xj) |
l(xj) *10^3 |
F(xLj) |
|
F(xPj) |
|
|
1 |
0 |
--- |
56 |
28 |
1 |
0,0295 |
0,00026 |
1,000 |
0,03 |
0,000 |
--- |
0,002 |
0,0024 |
0,36 |
2 |
56 |
--- |
112 |
84 |
1 |
0,3395 |
0,00887 |
0,991 |
0,34 |
0,002 |
--- |
0,022 |
0,0199 |
13,00 |
3 |
112 |
--- |
168 |
140 |
6 |
1,0222 |
0,04534 |
0,955 |
1,07 |
0,022 |
--- |
0,080 |
0,0579 |
32,26 |
4 |
168 |
--- |
224 |
196 |
36 |
1,9767 |
0,12855 |
0,871 |
2,27 |
0,080 |
--- |
0,191 |
0,1107 |
26,62 |
5 |
224 |
--- |
280 |
252 |
112 |
2,9147 |
0,26650 |
0,733 |
3,97 |
0,191 |
--- |
0,353 |
0,1622 |
0,77 |
6 |
280 |
--- |
336 |
308 |
201 |
3,4373 |
0,44717 |
0,553 |
6,22 |
0,353 |
--- |
0,544 |
0,1908 |
23,42 |
7 |
336 |
--- |
392 |
364 |
211 |
3,2650 |
0,63827 |
0,362 |
9,03 |
0,544 |
--- |
0,725 |
0,1813 |
41,37 |
8 |
392 |
--- |
448 |
420 |
127 |
2,4714 |
0,80102 |
0,199 |
12,42 |
0,725 |
--- |
0,863 |
0,1379 |
5,38 |
9 |
448 |
--- |
504 |
476 |
45 |
1,4613 |
0,91101 |
0,089 |
16,42 |
0,863 |
--- |
0,946 |
0,0824 |
4,56 |
10 |
504 |
--- |
560 |
532 |
9 |
0,6579 |
0,96874 |
0,031 |
21,05 |
0,946 |
--- |
0,983 |
0,0377 |
13,17 |
11 |
560 |
--- |
616 |
588 |
1 |
0,2191 |
0,99167 |
0,008 |
26,31 |
0,983 |
--- |
0,996 |
0,0129 |
7,78 |
|
|
|
|
Suma |
750 |
|
|
|
|
|
|
|
0,9962 |
168,68 |
Na podstawie rozkładu Weibulla dla x0 = 0 określiłem wartości parametrów x1, x2, x3 dzięki którym wyznaczyłem wartość parametru progowego x0
x1 = 115
x2 = 200
x3 = 340
x0= -16,36
Następnie z wykresu wyznaczyłem parametr kształtu i skali:
Nr. Przedziału |
Środek przedziału |
|
Funkcja zawodności (dystrybułanta) |
LN(Xj-Xo) |
LN(LN(1/(1-F(Xj)))) |
j |
Xj |
Xj-Xo |
F(Xj) |
|
|
1 |
28 |
44,3636364 |
0,001 |
3,792 |
-6,619 |
2 |
84 |
100,363636 |
0,003 |
4,609 |
-5,926 |
3 |
140 |
156,363636 |
0,011 |
5,052 |
-4,535 |
4 |
196 |
212,363636 |
0,059 |
5,358 |
-2,806 |
5 |
252 |
268,363636 |
0,208 |
5,592 |
-1,456 |
6 |
308 |
324,363636 |
0,476 |
5,782 |
-0,437 |
7 |
364 |
380,363636 |
0,757 |
5,941 |
0,348 |
8 |
420 |
436,363636 |
0,927 |
6,078 |
0,960 |
9 |
476 |
492,363636 |
0,987 |
6,199 |
1,463 |
10 |
532 |
548,363636 |
0,999 |
6,307 |
1,890 |
11 |
588 |
604,363636 |
1,000 |
6,404 |
|
A = 3,7887 B = -22,44
Parametr skali: a = 373,5
Parametr kształtu: b = 3,7887
Dla rozkładów Weibulla wartości krytyczne dla tych rozkładów są mniejsze od wartości otrzymanych w wyniku badania. Wynika z tego że rozkłady te nie mogą zostać przyjęte.
Dla rozkładu Weibulla dla Xo= -16,36 wartość krytyczna rozkładu χ2 = 14,067
a wartość dla rozkładu wynosi χ2 = 93,059
Dla rozkładu Weibulla dla Xo= 0 wartość krytyczna wynosi: χ2 = 15,507 a wartość dla rozkładu wynosi χ2 = 168,682.
W obydwu przypadkach wartości dla zadanych rozkładów przekraczają wartości graniczne, co powoduje, że hipotezy nie są prawdziwe.
Dany rozkład daje się opisać tylko za pomocą rozkładu normalnego ponieważ test zgodności χ2 (chi-kwadrat) dla rozkładu Weibulla nie zakończył się powodzeniem, χ2 otrzymaliśmy większe od wartości krytycznej.
Poniższe wykresy przedstawiają graficzny opis podstawowych miar niezawodności:
Określenie zasobów 90% i 50%
- dla rozkładu normalnego
γ90% = kwantyl rzędu (1- γ /100) = x0,1
u0,1 = (x0,1 - μ)/s
x0,1 = μ+ s u0,1
dla γ90% : u0,1 = -1,28 x0,1 = 242,3
dla γ50% : u0,5 = 0 x0,5 = 340,1
- dla rozkładu Weibulla Xo= -16,36
![]()
γ90% = kwantyl rzędu (1- γ /100) = x0,1
xγ =
a = 373,48
b = 3,79
x0 = -16,36
dla γ90% : x0,1 = 189,8
dla γ50% : x0,5 = 449,1
Określenie przedziału ufności dla odchylenia standardowego przy zadanym poziomie istotności α = 0,05
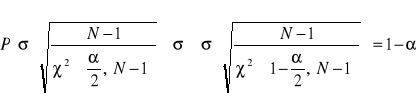
α/2 = 0,025
1 - α/2 = 0,975
N = 749
χ2(α/2 ; N-1) = 826,7
χ2(1 - α/2 ; N-1) = 675,1
- dla rozkładu normalnego
72,76 < σ < 80,52 σ = 76,4
- dla rozkładu Weibulla Xo= 0
105,03 < σ < 116,23 σ = 110,3
- dla rozkładu Weibulla Xo= -16,36
94,65 < σ < 104,75 σ=99,4
Określenie przedziału ufności dla wartości średniej przy zadanym poziomie istotności α = 0,05

α = 0,05
r = 749
t(α,r)=1,9631
- dla rozkładu normalnego
334,62 < µ < 345,59
µ = 340,1 σ =76,4
- dla rozkładu Weibulla Xo= 0
316,57 < µ < 332,4
µ=324,5 σ = 110,3
- dla rozkładu Weibulla Xo= -16,36
314 < µ < 328,26
µ = 321,1 σ =99,4
![]()
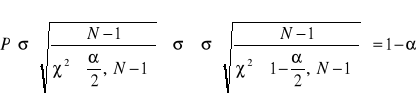
Wyszukiwarka
Podobne podstrony:
Praca PEiN, PW SiMR, Inżynierskie, Semestr VI, PEiN
k2nasze, PW SiMR, Inżynierskie, Semestr VI, Laborka KN
Wnioski do spr z elektry 3, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Lab. Ukł. Napędowych
Karta techn, PW SiMR, Inżynierskie, Semestr V, syf2, tbmm, TBM-projekt, 2 projekt, siela
ProtokółN2, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Lab. Ukł. Napędowych
TR-pytania, PW SiMR, Inżynierskie, Semestr V, syf2, pojazdy
rozne pytania na kolosy, PW SiMR, Inżynierskie, Semestr VII, Jakość
Wnioski e1, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Lab. Ukł. Napędowych, sprawko napedy
Obliczenia normy czasu dla otworu fi 8, PW SiMR, Inżynierskie, Semestr V, syf2, tbmm, TBM-projekt, 2
ACOVER, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, TeoRuch
A-rys1-10, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, TeoRuch
A-Rzdz3, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, TeoRuch
ROZDZ 8U, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, MTMT
COVER, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, MTMT
Podnosnik AZ, PW SiMR, Inżynierskie, Semestr V, syf2, PKM 2 projekt, pkm 2 wałek, projekty
Temat nr 1 jj 2011, PW SiMR, Inżynierskie, Semestr V, syf2, projektowanie silnika
ROZDZ 8K, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, MTMT
A-Intrdc, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, TeoRuch
więcej podobnych podstron