Politechnika Warszawska

Wydział Samochodów i Maszyn Roboczych

Instytut Maszyn Roboczych Ciężkich

Laboratorium Konstrukcji Nośnych

Sprawozdanie K2

Temat: Skręcanie profili cienkościennych

Opracowała Gr. 3..2 zespół 1

Adrian Kozak

Piotr Lange

1. Cel ćwiczenia.

Celem ćwiczenia było porównanie wpływu kształtu i rodzaju (otwarty i zamknięty) na wielkość kąta skręcenia i naprężeń stycznych. Oraz porównaniu metod doświadczalnych i analitycznych otrzymywania tych wielkości.

2. Stanowisko badawcze.

Badanie polegało na zawieszaniu kolejnych ciężarków na ramieniu przykręconym do badanego profilu, który był zamocowany z jednej strony nieruchomo do ramy a od strony przymocowania ramienia w sposób umożliwiający ruch obrotowy względem osi wzdłużnej profilu.

3. Kształt profilu.

- profil otwarty

- profil zamknięty

Oba profile miały długość l = 1080mm.

4. Wyniki pomiarów.

Pomiary dokonywaliśmy na ramieniu R = 530mm a ciężarki zawieszaliśmy na ramieniu

r = 510mm przyspieszenie ziemskie g = 9,81m/s².

	Obciążenie [kg]	Obciążenie [N]	Ugięcie [mm]
Profil otwarty	4.64	45.518	40
		5.58	54.740	50
		6.56	64.354	56
	Profil zamknięty	14.56	142.834	5
		21.42	210.130	8
		31.42	308.230	10

5. Charakterystyka geometryczna przekroju.

- profil zamknięty

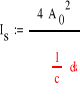
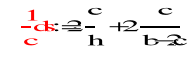
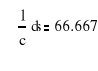
- profili otwarty

6. Wyznaczenie momentów skręcających.

 

	Obciążenie [kg]	Obciążenie [N]	Moment skręcający Ms[N*m]
Profil otwarty	4,64	45,5184	23,214384
		5,58	54,7398	27,917298
		6,56	64,3536	32,820336
	Profil zamknięty	14,56	142,8336	72,845136
		21,42	210,1302	107,166402
		31,42	308,2302	157,197402

Do obliczeń korzystamy ze wzoru:

Ms = Obciążenie * r gdzie r = 510mm

7. Wyznaczenie kąta skręcenia na postawie analizy wyników doświadczalnych.

	Ugięcie [mm]	sinφ	φ[rad]	φ[°]
Profil otwarty	40	0,075472	0,075544	4,328329
		50	0,09434	0,09448	5,413317
		56	0,10566	0,105858	6,06522
	Profil zamknięty	5	0,009434	0,009434	0,540535
		8	0,015094	0,015095	0,864876
		10	0,018868	0,018869	1,081118

Do obliczenia korzystamy z następujących wzorów:

sinφ = ugięcie/ R gdzie R = 530mm

φ = asin( ugięcie/R)

8. Wyznaczenie kąta skręcenia na podstawi wzorów algebraicznych.

	Moment skręcający Ms[N*m]	φ[rad]	φ[°]
Profil otwarty	23,214384	0,23989	13,7516946
		27,917298	0,28849	16,5375982
		32,820336	0,33916	19,4420510
	Profil zamknięty	72,845136	0,00256	0,1466101
		107,166402	0,00376	0,2156861
		157,197402	0,00552	0,3163799

Do obliczeń wykorzystano wzory

- profil otwarty

- profil zamknięty

gdzie E = 2,1 E11 [N/m²] υ = 0,3

9. Porównanie wyników analitycznych i doświadczalnych kąta skręcenia φ w funkcji momentu skręcającego Ms.

10. Obliczenie maksymalnych naprężeń stycznych.

	Moment skręcający Ms[N*m]	Naprężenia max [Pa]	Naprężenia max [MPa]
Profil otwarty	23,214384	27418563,78	27,41856378
		27,917298	32973186,61	32,97318661
		32,820336	38764176,38	38,76417638
	Profil zamknięty	72,845136	4864125	4,864125
		107,166402	7155876,202	7,155876202
		157,197402	10496621,39	10,49662139

Do obliczeń korzystamy ze wzorów:

- profil otwarty

gdzie ρ = c/2

- profil zamknięty

gdzie

11. Wyznaczenie położenia środka skręcenia.

- profil zamknięty

Korzystając z zależności, że dla przekrojów posiadających oś symetrii środek skręcenia leży na tej osi. Możemy stwierdzić, że dla profilu zamkniętego środek skręcenia znajduje się w punkcie przecięci się osi symetrii boków.

- profil otwarty

Ze względu na istnienie osi symetrii nie jest konieczne obliczanie położenia środka symetrii względem osi z. Znajduje się on na osi.

Przyjmujemy punkt b w początku układu współrzędnych.

y_b = 0

Ze względu na symetrię możemy rozpatrzyć połowę przekroju:

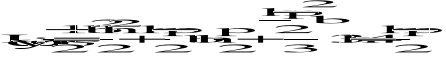
12. Wnioski:

Na podstawie przeprowadzonego ćwiczenia można zauważyć, że przy zbliżonym kształcie przekrojów duży wpływ zarówno na kąt skręcenia jak i naprężenia styczne ma rodzaj przekroju (otwarty czy zamknięty). Dla przekroju otwartego kąty skręcenia są ponad dziesięciokrotnie większe od kątów dla przekroju zamkniętego.

Różnice pomiędzy wartościami analitycznymi i doświadczalnymi są duże ze względu, że w ćwiczeniu uwzględnialiśmy jedyni skręcanie swobodne z pominięciem deplanacji. Niedokładności wynikały także z niedokładności dokonywania pomiarów.

---