Statystyka może być rozumiana dwojako, w sensie potocznym uważa się za nią niektóre zestawienia liczbowe charakteryzujące np. umieralność niemowląt, wydobycie kopalin, wypadki przy pracy, spożycie dobra na jednostkę itp. Tak pojmowana statystyka nie jest dyscypliną naukową. Przez statystykę bowiem rozumiemy naukę, która zajmuje się badaniem prawidłowości zachodzących w procesach masowych.

Procesy masowe rządzą się prawami wielkich liczb (na 1000 dzieci rodzi się 517 chłopców i 483 dziewczynki), nie mówimy o nich gdy mamy do czynienia z jednym i tylko jednym przypadkiem (w jednej rodzinie urodziły się cztery dziewczynki)

Prawidłowości statystyczne są wynikiem występowania tzw. przyczyn głównych, prawidłowości są odkształcane (zakłócane) poprzez występowanie przyczyn ubocznych, im większa jest liczba obserwacji tym mniejsze jest oddziaływanie przyczyn ubocznych, a gdy liczba obserwacji dąży do nieskończoności oddziaływanie przyczyn ubocznych wzajemnie się znosi (spada do zera).

Zadania statystyczne

Podstawowym zadaniem statystycznym jest dostarczanie wiarygodnych informacji w celu zarządzania wszystkimi dziedzinami życia.

Podział statystyki (wg różnych kryteriów)

Statystyka matematyczna

Zajmuje się weryfikacją hipotez statystycznych oraz estymacją (szacowaniem) punktową lub przedziałową parametrów.

Statystyka opisowa

Główne działy statystyki opisowej

Kompleksowa analiza struktury zbiorowości,

Analiza korelacji i regresji,

Analiza dynamiki zjawisk (badanie szeregów czasowych, tendencji rozwojowej).

Podstawowe pojęcia

ZNAKI UMOWNE
-	Zjawisko nie występuje
0,0	Zjawisko występuje w ilościach mniejszych niż da się to wyrazić w przyjętej jednostce miary
.	Brak danych lub brak danych wiarygodnych
X	Wypełnienie rubryki nie dotyczy, nie ma sensy

Zbiorowość statystyczna - nie definiujemy - stanowi odpowiednik zbioru w matematyce, podajemy jednak przykłady zbiorowości np. zbiorowość osób, przedmiotów, zjawisk (przyrodniczych, ekonomicznych, społecznych). Zbiorowość zwana inaczej populacją albo zbiorowością generalną składa się z jednostek statystycznych (odpowiedniki elementów w zbiorze). Każda jednostka zbiorowości ma pewne właściwości. Te właściwości nazywamy cechami statystycznymi - to one podlegają badaniu.

Ogólny podział cech statystycznych

Stałe,

Wspólne wszystkim jednostkom statystycznym i z uwagi na to nie są przedmiotem badania a tylko odpowiedniego grupowania zbiorowości na pewne podzbiorowości.

Zmienne,

Rozróżniają jednostki pomiędzy sobą. Dzielą się na:

cechy mierzalne inaczej ilościowe (takie, których wartość da się przedstawić za pomocą liczby).Wśród mierzalnych wyróżnia się cechy:

ciągłe, ich wartości przedstawia się w postaci dowolnej liczby rzeczywistej np. wiek, waga, wydajność pracy, cena, kurs, temperatura,

skokowe, ich wartość da się przedstawić wyłącznie za pomocą zera lub liczb naturalnych (np. liczba dzieci w rodzinie 0, 1, 2, 3...)

quasi ciągłe

cechy niemierzalne (jakościowe) to takie cechy, których wartości nie da się zmierzyć a jedynie opisać w sposób słowny (płeć, wykształcenie, kolor włosów).

Kompleksowa analiza struktury zbiorowości

W skład kompleksowej analizy struktury zbiorowości wchodzą:

Średnia (klasyczna i pozycyjna),

Miary rozproszenia (dyspersji),

Miary skośności (asymetrii),

Miary spłaszczenia (koncentracji).

Ad.1 Średnie klasyczne

Średnia arytmetyczna (średnia x -
)

dla szeregów prostych gdy dane nie są uporządkowane wyraża się wzorem

x_i - wartość badanej cechy i-tej jednostki statystycznej,

N - liczba badanych jednostek statystycznych.

PRZYKŁAD :

Średni wzrost mężczyzn (10 elementów)

x₁ = 168 x₂ = 178 x₃ = 171 x₄ = 185 x₅ =180

x₆ = 171 x₇ = 179 x₈ =183 x₉ =180 x₁₀ =175

= 177 cm

dla szeregu rozdzielczego - jeżeli w wyniku odpowiedniego grupowania danych nieuporządkowanych w szereg rozdzielczy w postaci:

x	ni	x`i	ni ⋅x`i
700-800	11	750	8250
800-900	18	850	15300
900-1000	26	950	24700
1000-1800	36	1400	50400
1800-2400	32	2100	67200
2400-3000	16	2700	43200
suma	N=139		209050

n_i - liczebność i-tego przedziału klasowego (suma n_i równa się N)

x`_i - środek i-tego przedziału klasowego

średnia geometryczna

stosujemy dla liczb względnych (procenty, promile np. roczne wykonanie planu).

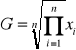
gdzie x_i >0 (PI oznacza iloczyn)

średnia harmoniczna

jest odwrotnością średniej arytmetycznej - stosujemy gdy dane są podane jako odwrotność np. zużycie paliwa na jednostkę, wydajność na godzinę.

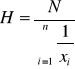
gdzie x_i ≠0

Ad. 1 Średnie pozycyjne

Wynikają z pozycji w szeregu, wyznacza się na podstawie tzw. wzorów interpolacyjnych.

Dominanta (wartość typowa , modalna, dominująca) - to taka wartość badanej cechy, której odpowiada największa liczebność

Sposób wyznaczania dominanty dla szeregu prostego

uporządkować szereg rosnąco (czasami malejąco),

podsumować jednostki, które maja tę samą wartość.

Dominantą będzie wartość występująca najczęściej.

Sposób wyznaczania dominanty dla szeregu rozdzielczego

gdzie: x_o - dolna granica przedziału w którym znajduje się dominanta,

c_o - rozpiętość przedziału dominanty,

n_d - liczebność przedziału, w którym znajduje się dominanta,

n_d-1 - liczebność przedziału poprzedzającego,

n_d+1 - liczebność przedziału następnego po przedziale dominanty.

Dominantę z szeregu rozdzielczego można w przybliżeniu wyznaczyć także w sposób graficzny.

Mediana (wartość środkowa)

Kwartyl 1 - Q₁ to taka wartość badanej cechy, która dzieli populację na dwie części w sposób następujący - 25% jednostek statystycznych jeszcze tej wartości nie osiągnęło a pozostałe 75% tę wartość przekroczyło.

Kwartyl 2 - Q₂ - Me (mediana) to taka wartość badanej cechy, która dzieli populację na połowy, inaczej mówiąc jest to wartość środkowa. W medianie połowa populacji jeszcze nie osiągnęła wartości badanej cechy a druga połowa już tę wartość przekroczyła.

Kwartyl 3 - Q₃ to taka wartość badanej cechy, której 75% liczebności jeszcze nie osiągnęło tej wielkości a 25% ją przekroczyło.

Sposób wyznaczania mediany dla szeregu prostego

uporządkować dane w sposób rosnący,

zauważyć (przeliczyć) czy liczba obserwacji jest parzysta czy nieparzysta

Jeżeli szereg jest nieparzysty wartość mediany stanowi wartość cechy wyrazu środkowego

168, 178, 171, 185, 180, 171, 179, 183, 180, 175, 186

168, 171, 171, 175, 178, 179, 180, 180, 183, 185, 186

Me = 179

Jeżeli szereg jest parzysty są dwa wyrazy środkowe a medianę stanowi średnia arytmetyczna wartości badanej cechy wyznaczona z obu wyrazów środkowych

159, 168, 171, 171, 175, 178, 179, 180, 180, 183, 185, 186

Me = (178+179) ÷ 2 = 178,5 ≈ 179

Mediana dla szeregu rozdzielczego:

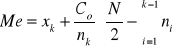
gdzie: x_k = dolna granica przedziału, w którym znajduje się mediana (początek przedziału),

C_o = rozpiętość przedziału, w którym znajduje się mediana (długość przedziału),

n_k = liczebność przedziału, w którym znajduje się mediana (wielkość odpowiadająca przedziałowi),

k-1 = suma n_i od początku do przedziału z medianą.

N/2 (a gdy liczba obserwacji jest nieparzysta (N+1)/2 - oznacza pozycję mediany w szeregu

Miary dyspersji (rozproszenia - zróżnicowania zjawiska)

Najprostszą miarą dyspersji jest rozstęp oznaczający różnicę pomiędzy wartością minimalną a maksymalną badanej cechy

R = x_max - x_min

Przykład:

Jeżeli w przedsiębiorstwie najwyższa płaca wynosi 4.800 zł. A najniższa 800 zł. To rozstęp wynosi 4.800 - 800 = 4.000 zł.

Odchylenie przeciętne

dla szeregu prostego ma postać:

dla szeregu rozdzielczego ma postać:

Odchylenie standardowe:

dla szeregu prostego ma postać:

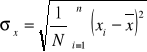
dla szeregu rozdzielczego ma postać:

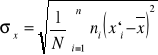
Odchylenie ćwiartkowe (stosujemy dla mediany)

Współczynnik zmienności jest miarą „dobroci” średniej (arytmetycznej)

jeżeli: V_x ≤ 35% to średnia jest „bardzo dobra” (bardzo dobrze opisuje badaną rzeczywistość),

35% ≤ V_x ≤ 68% to średnia jest „dobra”,

68% ≤ V_x ≤ 75% to średnia jest „do przyjęcia”,

V_x > 75% to średnia traci swój sens poznawczy.

Miary skośności (asymetrii)

b - rozkład symetryczny (osią symetrii byłaby rzędna)

a, c - rozkłady asymetryczne; a - ma asymetrię lewostronną, c - asymetrię prawostronną

Najprostszą miarą asymetrii jest różnica pomiędzy średnią arytmetyczną a dominantą.

R_b =x - D = 0

R_a =x - D < 0 rozkład o asymetrii ujemnej

R_c =x - D > 0 rozkład o asymetrii dodatniej

Wzajemne położenie średniej, dominanty i Mediany w rozkładzie

Przy asymetrii ujemnej średnia arytmetyczna jest zaniżona, przy asymetrii dodatniej średnia arytmetyczna jest zawyżona.

Mierniki asymetrii

Nasilenie asymetrii możemy mierzyć dwojako:

Jako tzw. współczynnik asymetrii

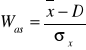
i zawiera się -1 ≤ W_as ≤ 1

Za pomocą wyrażenia:

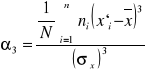
i zawiera się -2 ≤ α₃ ≤ 2

Miary spłaszczenia (koncentracji wokół średniej)

Mierzymy ją wzorem:

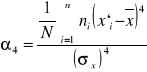
Rozkład normalny - funkcja Gaussa.

Mamy z nią do czynienia gdy jednocześnie α₃ = 0 i α₄ = 3 i ma kształt symetryczny - dzwonowaty.

(wiadomo, że gdy α₃=0 rozkład jest symetryczny).

Funkcja Gaussa ma postać:

( e ≈ 2,72 )

Okazuje się, że:

Regóła trzech “sigm”:

W przedziale (-3σ,3σ) mieszczą się (zawierają się) prawie wszystkie badane jednostki statystyczne.

W przedziale (-2σ,2σ) znajduje się ponad 95% wszystkich badanych jednostek ststystycznych.

W przedziale (-σ,σ) znajduje się około 68% wszystkich badanych jednostek ststystycznych.

Przedział x - σ_x ≤ x_typ ≤ x + σ_x nazywamy “x - typowym”.

Charakterystyka średnich:

Średnia arytmetyczna:

obliczana na podstawie wszystkich danych szeregu,

na jej wartość duży wpływ mają wielkości skrajne,

nadaje się do przekształceń algebraicznych,

suma odchyleń od średniej równa się zeru (0).

Średnia harmoniczna:

obliczana na podstawie wszystkich danych szeregu,

nadaje się do przekształceń algebraicznych,

stosujemy głównie wtedy, gdy mamy do czynienia z odwrotnościami jakiejś wielkości.

Średnia geometryczna:

obliczana na podstawie wszystkich danych szeregu,

wartości skrajne mają na nią mniejszy wpływ niż na średnią arytmetyczną,

jest mniejsza od średniej arytmetycznej,

istnieje dla x_i > 0,

jest pomocna przy obliczaniu średnich wskaźników.

Dominanta:

jest wartością najbardziej typową dla szeregu,

łatwo ją wyznaczyć z uporządkowanego szeregu prostego,

dla szeregu rozdzielczego można ją tylko oszacować,

przy małej liczebności może nie być dominanty, a przy dużej może wystąpić więcej niż jedna dominanta (przy dwóch dominantach szereg nazywamy bimodalnym).

Mediana:

nie mają na nią wpływu wartości skrajne,

stosuje się głównie dla szeregów skrajnie asymetrycznych.

Warunki stosowania parametrów opisowych:

Względna jednorodność zbiorowości ze względu na badaną cechę (analiza V_x ; najlepiej, gdy V_x ≤ 35%, gdy współczynnik jest nie większy niż 75%).

Gdy jest niewielka asymetria rozkładu (przy dużej asymetrii x arytmetyczna nie ma wartości poznawczej).

Nie stosujemy średniej gdy szereg nie jest domknięty dołem i górą.

Nie stosujemy mediany gdy szereg ma przedziały o różnej rozpiętości.

Dla rozkładów o dużej asymetrii stosujemy wyłącznie przeciętne pozycyjne ( dominanta i kwartyle [Me]}

W październiku 1999 r. Na pewnym lokalnym rynku nieruchomości zanotowano następujące ceny ofertowe mieszkań:

Cena w tys. zł.	Liczba mieszkań
60 - 70	1
70 - 80	3
80 - 90	20
90 - 100	26
100 - 110	14
110 - 120	12
120 - 130	10
130 - 140	7
140 - 150	5
150 - 160	2
Razem	100

Zbiorowość - liczba mieszkań.

Jednostka statystyczna - jedno mieszkanie.

Badana cecha - cena (x)

Kompleksowe badanie polega na:

Sporządzić wykres (histogram) - przez co uzyskamy odpowiedź na asymetrię i wzajemne położenie średniej, dominanty i mediany,

Obliczyć średnią arytmetyczną,

Sprawdzić jej „dobroć” za pomocą odchylenia standardowego i współczynnika zmienności,

Obliczyć rozstęp,

Wyznaczyć dominantę i medianę,

Zbadać asymetrię rozkładu, skośność,

Zbadać spłaszczenie rozkładu (koncentrację wokół średniej),

Wyznaczyć obszar typowy.

x = 105,4 Me = 100 D = 93,3 σ_x = 19,85

R = 100 Po = 8,8 v_x = 18,83% W_as = - 0,61

105,4 - 19,85 = 85,55 105,4 + 19,85 = 125,25 85,55 < x-typowe < 125,25

Najpotrzebniejsze informacje:

Średnia arytmetyczna i jej interpretacje (przekłamuje).

Mediana (interpretacja).

Miary dyspersji, odchylenie standardowe.

Czemu służy współczynnik zmienności, co wiemy dzięki niemu.

Interpretacja przedziału typowego i z czego to wynika.

Czemu służy histogram, jak w przybliżeniu wyznaczyć dominantę.

Odróżnić zbiorowość statystyczną, jednostkę statystyczną i badaną cechę (umieć opisać cechę: niemierzalna, mierzalna - ciągła i skokowa.

UWAGA : Zbiór wszystkich badanych cech statystycznych nazywamy zakresem badania.

Analiza korelacji i regresji.

O korelacji mówimy, wtedy jeżeli średnim wartościom jednej cechy ściśle odpowiadają wartości drugiej cechy.

(funkcja - każdej wartości x odpowiada tylko jedna wartość y).

Wyróżnia się korelację liniową lub krzywoliniową - wśród której wyróżniamy korelację dwóch lub wielu cech statystycznych. Gdy objaśniamy jedną cechę (objaśnianą) całym zbiorem cech (objaśniających) to mamy do czynienia z korelacją wieloraką.

Jeżeli natomiast chcemy znać rzeczywistą współzależność pomiędzy dwoma cechami z wyeliminowaniem wpływu pozostałych cech to mamy do czynienia z tzw. korelacją cząstkową.

Dalsze rozważania ograniczamy do korelacji liniowej dwóch cech.

Prosty związek (współzależność) pomiędzy dwoma cechami statystycznymi można zbadać (zaobserwować) na podstawie tzw. diagramów korelacyjnych (wykresów korelacyjnych).

UWAGA : Badanie współzależności dwóch cech przeprowadzamy wtedy i tylko wtedy jeżeli pomiędzy tymi cechami zachodzi związek logiczny. (np. im wyższe wykształcenie tym wyższe kwalifikacje, ale nie koniecznie odwrotnie).

Równania regresji dwóch zmiennych służą do oszacowania średniej wielkości jednej zmiennej.

Diagram (C) wykazuje, że pomiędzy cechami (x) i (y) nie zachodzi żadna korelacja.

Diagram (D) mówi, że pomiędzy cechami (x) i (y) zachodzi korelacja krzywo-liniowa.

Diagramy (A) i (B) wskazują na istnienie korelacji liniowej. W przypadku diagramu (A) dodatniej a w diagramie (B) ujemnej.

Korelacja dodatnia oznacza związek wprost proporcjonalny, w którym wraz ze wzrostem wartości jednej cechy rośnie wartość cechy drugiej.

Korelacja ujemna oznacza związek odwrotnie proporcjonalny, w którym wraz ze wzrostem wartości jednej cechy maleje wartość cechy drugiej.

Korelację liniową mierzy się za pomocą współczynnika korelacji liniowej Pearsona, która ma postać:

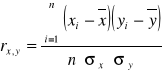
Właściwości współczynnika :

r_x,y = r_y,x korelacja pomiędzy (x) a (y) jest taka sama jak pomiędzy (y) a (x).

-1 ≤ r_x,y ≤ 1

Jeżeli r = ± 1 to mamy do czynienia z zależnością funkcyjną, matematyczną.

Jeżeli 0 < r < 1 to mamy do czynienia ze związkiem wprost proporcjonalnym.

Jeżeli - 1 < r < 0 to mamy do czynienia ze związkiem odwrotnie proporcjonalnym.

Jeżeli r jest nie większa niż 0,3 to mówimy, że korelacja jest niewyraźna.

Jeżeli r jest większa niż 0,3 a mniejsza niż 0.5 to mówimy, że korelacja jest średnia.

Jeżeli r jest większa niż 0,5 to mówimy, że korelacja jest wyraźna.

Równanie regresji liniowej dwóch zmiennych ma zastosowanie wtedy gdy mając dane dla jednej cechy można w przybliżeniu określić średnie wielkości lub wartości drugiej cechy.

Zależność cechy (y) od cechy (x) można wyrazić za pomocą następujących równań regresji:

1.
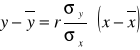
po przekształceniu otrzymamy

2. y = a + bx

Zależność cechy (x) od cechy (y) można wyrazić za pomocą następujących równań regresji:

3.
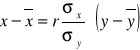
po przekształceniu otrzymamy

4. x = a + by

UWAGA : Kierunek regresji w obu równaniach (2 i 4) zależy wyłącznie od współczynnika (b). (a) nie ma związku ze współczynnikiem korelacji.

Wzajemne położenie linii regresji:

Jeżeli oba równania się pokrywają to korelacja przekształca się w związek funkcyjny (czyli r = -1 lub r = 1).

Jeżeli α = 90° to r = 0 więc nie ma korelacji

Szacując jedną cechę na podstawie drugiej popełnia się tzw. błędy standardowe szacunku:

Dla równania (2)

Dla równania (4)

Korelacja - współzależność 2 cech

Przykład

W 20 losowo wybranych mieszkaniach zaobserwowano następujące relacje pomiędzy liczbą pokoi w mieszkaniu a liczbą zamieszkujących te pokoje osób.

Liczba pokoi (y)	7	1	5	4	2	3	6	5	4	3	2	2	1	3	5	4	5	3	4	1
Liczba osób (x)	6	1	6	4	2	2	5	4	3	3	3	1	3	4	4	4	5	4	5	1

Zbadać czy pomiędzy wymienionymi cechami zachodzi liniowy związek korelacyjny.

Oszacować wielkość mieszkania (liczbę pokoi) dla rodziny liczącej 4 osoby.

Z wykresu korelacyjnego wynika, że mamy do czynienia z istotnym, liniowym, dodatnim związkiem korelacyjnym. Oznacza to, że korelacja ma charakter wprost proporcjonalny, gdzie wraz ze wzrostem liczby osób w rodzinie rośnie ilość zajmowanych przez tę rodzinę pokoi (z układu punktów wynika, że współczynnik korelacji musi mieć znak dodatni (+), a wartość współczynnika musi być powyżej 0,6.

Ponieważ korelacja jest widoczna można przystąpić do oszacowania wielkości mieszkania dla 4 osobowej rodziny (szacujemy „y”).

Korzystamy w tym celu z linii regresji szacującej na podstawie której oszacujemy średnią wielkość (y) na podstawie (x = 4).

x	y	x -x	y -y	(x -x)⋅(y -y)	(x -x)^2	(y -y)^2
6	7	2,50	3,50	8,75	6,25	12,25
1	1	-2,50	-2,50	6,25	6,25	6,25
6	5	2,50	1,50	3,75	6,25	2,25
4	4	0,50	0,50	0,25	0,25	0,25
2	2	-1,50	-1,50	2,25	2,25	2,25
2	3	-1,50	-0,50	0,75	2,25	0,25
5	6	1,50	2,50	3,75	2,25	6,25
4	5	0,50	1,50	0,75	0,25	2,25
3	4	-0,50	0,50	-0,25	0,25	0,25
3	3	-0,50	-0,50	0,25	0,25	0,25
3	2	-0,50	-1,50	0,75	0,25	2,25
1	2	-2,50	-1,50	3,75	6,25	2,25
3	1	-0,50	-2,50	1,25	0,25	6,25
4	3	0,50	-0,50	-0,25	0,25	0,25
4	5	0,50	1,50	0,75	0,25	2,25
4	4	0,50	0,50	0,25	0,25	0,25
5	5	1,50	1,50	2,25	2,25	2,25
4	3	0,50	-0,50	-0,25	0,25	0,25
5	4	1,50	0,50	0,75	2,25	0,25
1	1	-2,50	-2,50	6,25	6,25	6,25
70	70	x	x	42,00	45,00	55,00

Średnia x x = 70 / 20 = 3,5

Średnia y y = 70 / 20 = 3,5

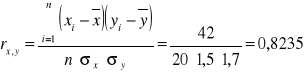
Obliczony współczynnik korelacji potwierdza istotną, liniową, dodatnia (wprost proporcjonalną) korelację pomiędzy wielkością rodziny i wielkością mieszkania. Logiczny związek pomiędzy tymi dwoma cechami oraz wysoki współczynnik korelacji sprawiają, że można przejść do oszacowania wielkości mieszkania dla 4 osobowej rodziny:

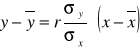
błąd oszacowania:

Wielkość mieszkania oszacowana przedziałowo z błędem (±1,02) pokoi wynosi (3,9 - 1,02 ; 3,9 + 1,02) czyli (3 ; 5)

Zadanie

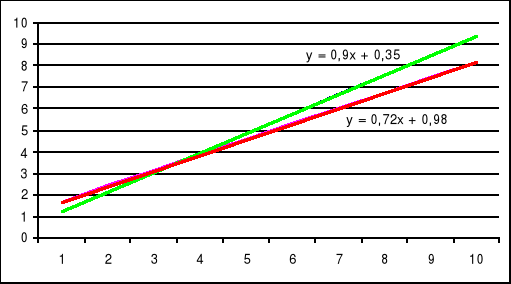
Wyznaczyć linie regresji dla (x) i narysować wspólny wykres.

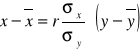
Badanie tendencji rozwojowej.

Tendencja rozwojowa -ogólna dążność zjawiska do wzrostu lub spadku. Bada się ją zwykle w okresach 10 i więcej lat. Warunkiem doboru okresu badania jest działanie tych samych przyczyn głównych. Ogólną tendencję rozwojową zakłóca działanie tzw. przyczyn ubocznych, które można w jakimś sensie zneutralizować poprzez tzw. wygładzanie szeregów chronologicznych. Są dwie metody wygładzania szeregów chronologicznych.

Metoda mechaniczna. Polega na zastosowaniu tzw. średnich ruchomych.

Jeżeli wartość zjawiska w kolejnych latach wynosi (y₁, y₂, y₃, y₁, ... y_n-1, y_n) to trzyletnie średnie ruchome mają postać

Następna średnia ruchoma powstanie z pierwszej przez opuszczenie wyrazu pierwszego i dodanie wyrazu czwartego

itd.

Ostatnia trzyelementowa średnia ruchoma mieć będzie postać:

Pięcioelementowe średnie ruchome tworzymy w analogiczny sposób pamiętając, że uśredniamy element środkowy:

Średnie ruchome umożliwiają eliminowanie z szeregu wahań przypadkowych. Im średnia ruchoma obejmuje więcej elementów tym bardziej są eliminowane przyczyny uboczne a szereg chronologiczny jest bardziej wygładzony.

Gdy liczba obserwacji jest parzysta średnia chronologiczna przybiera postać średniej ruchomej scentrowanej:

Zaletą metody mechanicznej jest to, iż umożliwia ona uzyskanie obrazu uwolnionego od działania czynników ubocznych, wadą natomiast jest po pierwsze skracanie szeregu chronologicznego, po drugie niemożność zapisu tendencji rozwojowej w postaci matematycznej, po trzecie niemożność ekstrapolacji (przewidywania) zjawiska w przyszłości.

Metoda analityczna. Polega na opisie tendencji rozwojowej za pomocą funkcji matematycznej zwanej aproksymantą, dobranej tak aby spełniony był warunek

Suma kwadratów odchyleń wartości empirycznych (doświadczalnych) i uzyskanych na podstawie aproksymanty ma być jak najmniejsza (aproksymanta ma odpowiadać klasycznej metodzie najmniejszych kwadratów).

Sposób postępowania:

Wyznaczyć na układzie współrzędnych wartości empiryczne zjawiska i na podstawie rozkładu punktów wybrać jedną z klas funkcji (kształt aproksymanty).

b > 0

b < 0

b = 0

a > 1

a > 1

t > 1

0 < a < 1

Oszacować parametry aproksymanty.

Oszacować „dobroć” aproksymanty.

Trend liniowy

W trendzie liniowym i w każdym innym trendzie jedyną determinantą rozwoju zjawiska jest czas.

W równaniu trendu liniowego w postaci

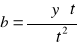
oznacza średni poziom zjawiska w badanym okresie,

okresowe (roczne) przyrosty zjawiska (wzrost dla b>0, spadek dla b<0)

Równanie trendu linowego można wyznaczyć w sposób uproszczony postępując w następujący sposób:

1. Jeżeli szereg chronologiczny składa się z nieparzystej liczby danych to za wartość (t) dla wyrazu środkowego wpisujemy zero (0). Począwszy od zera w kierunku wcześniejszych wartości wpisujemy w miejsce (t) odpowiednio (-1, -2, -3, ...), dla wartości późniejszych począwszy od zera w miejsce (t) wpisujemy kolejno (1, 2, 3, ...).

Przykład (dane umowne)

Szereg nieparzysty

lata	yt	t
1996	15	-3
1997	18	-2
1998	16	-1
1999	19	0
2000	22	1
2001	21	2
2002	24	3

Szereg parzysty

lata	yt	t	yt ⋅ t	t^2
1995	13	-7
1996	15	-5
1997	18	-3
1998	16	-1
1999	19	1
2000	22	3
2001	21	5
2002	24	7
	Σ	X	Σ	Σ

Miarą dobroci oszacowań (np. przewidywanie produkcji) wartości uzyskanych na podstawie funkcji trendów jest wyrażenie:

gdzie (K) jest liczbą parametrów funkcji

dla funkcji (y=a+bt) dwa parametry (a,b), dla funkcji (y= a²+bt+c) trzy parametry (a,b,c)

Podstawy Statystyki z przykładami

19

www.wkuwanko.pl

Dodać wszystkie wartości danych (x) i podzielić przez ich liczbę

168+178+171+185+180+171+179+183+180+175 = 1770

1770 ÷10 = 177

W kolumnie (x) podano przedziały zarobków.

W kolumnie (n_i) podano ilość osób które spełniają warunki kolumny (x).

W kolumnie (x`_i) obliczono środek przedziału klasowego

Np. (700+800) ÷ 2 = 750

W kolumnie (n_i⋅x`_i) podano iloczyn dwóch wcześniejszych kolumn.

UWAGA: wartości graniczne przypisujemy do wyższej klasy (np. wartość 800 przypisujemy do drugiej klasy)

209.050 ÷ 139 = 1504

Liczebność (% lub liczby rzeczywiste

Wartość badanej cechy (cecha mierzalna

Dominanta rzeczywiste

wartość rzeczywiste

Dominanta

x

n

skumulowany szereg liczebności do przedziału poprzedzającego przedział z medianą

UWAGA - odchylenie standardowe podniesione do potęgi drugiej nosi nazwę wariancji

(σ_x)² - wariancja

Środek przedziału klasowego

b

a

c

cecha

liczebność

b

a

c

x

n_i

D

D

Me

średnia

średnia

Me

D

Me

średnia

a

b

c

Największa koncentracja

Im bardziej układ wysmukły, tym mniejsze rozproszenie

punkty przegięcia

- σ_x

σ_x

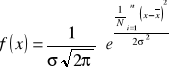
- σ_x

σ_x

- 2σ_x

- 3σ_x

3σ_x

2σ_x

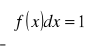
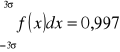
1. Określić zbiorowość, jednostkę statystyczną i badaną cechę.

2. Przeprowadzić kompleksową analizę cen ofertowych mieszkań.

60

70

80

90

100

110

120

130

140

150

160

A

B

C

D

r > 0

r < 0

r = 0

Korelacja krzywo linowa

y

y

y

y

x

x

Korelacja ujemna

Korelacja dodatnia

x

x

y

y

x

x

y =y

x =x

Błąd oszacowania

± Sy

pokoje

osoby

1

2

3

4

5

6

7

1

2

3

4

5

6

Współczynnik korelacji podajemy z dokładnością do 4 miejsc po przecinku

y[Author ID1: at Wed Jan 29 12:46:00 2003 ]

t[Author ID1: at Wed Jan 29 12:46:00 2003 ]

y[Author ID1: at Wed Jan 29 12:46:00 2003 ]

t[Author ID1: at Wed Jan 29 12:46:00 2003 ]

y[Author ID1: at Wed Jan 29 12:46:00 2003 ]

t[Author ID1: at Wed Jan 29 12:46:00 2003 ]

y[Author ID1: at Wed Jan 29 12:46:00 2003 ]

t[Author ID1: at Wed Jan 29 12:46:00 2003 ]

y[Author ID1: at Wed Jan 29 12:46:00 2003 ]

t[Author ID1: at Wed Jan 29 12:46:00 2003 ]

y[Author ID1: at Wed Jan 29 12:46:00 2003 ]

t[Author ID1: at Wed Jan 29 12:46:00 2003 ]

y[Author ID1: at Wed Jan 29 12:46:00 2003 ]

t[Author ID1: at Wed Jan 29 12:46:00 2003 ]

---