Rozkład zmiennej losowej

• Prawdopodobieństwo
• Rozkład normalny
• Przedział ufności

PODSTAWY

STATYSTYKI OPISOWEJ

Parametry

opisowe

zbiorowoś

ci

statystycz

nej

charakterystyki

liczbowe, dające

sumaryczny i

skrócony opis

zbiorowości

statystycznej.

Jeżeli na n osób m jest liczbą kobiet, to możemy
powiedzieć, że prawdopodobieństwo że x jest
kobietą, co zapiszemy P(x=kobieta) wynosi
m/n; 0<=P<=1

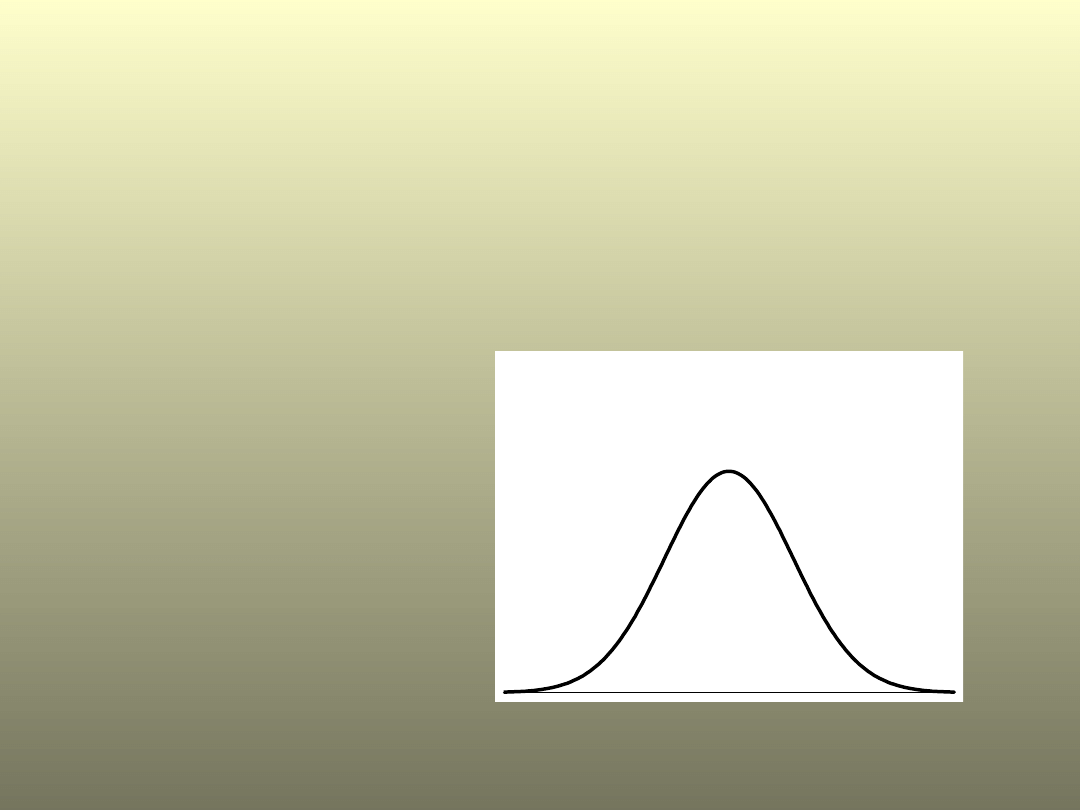
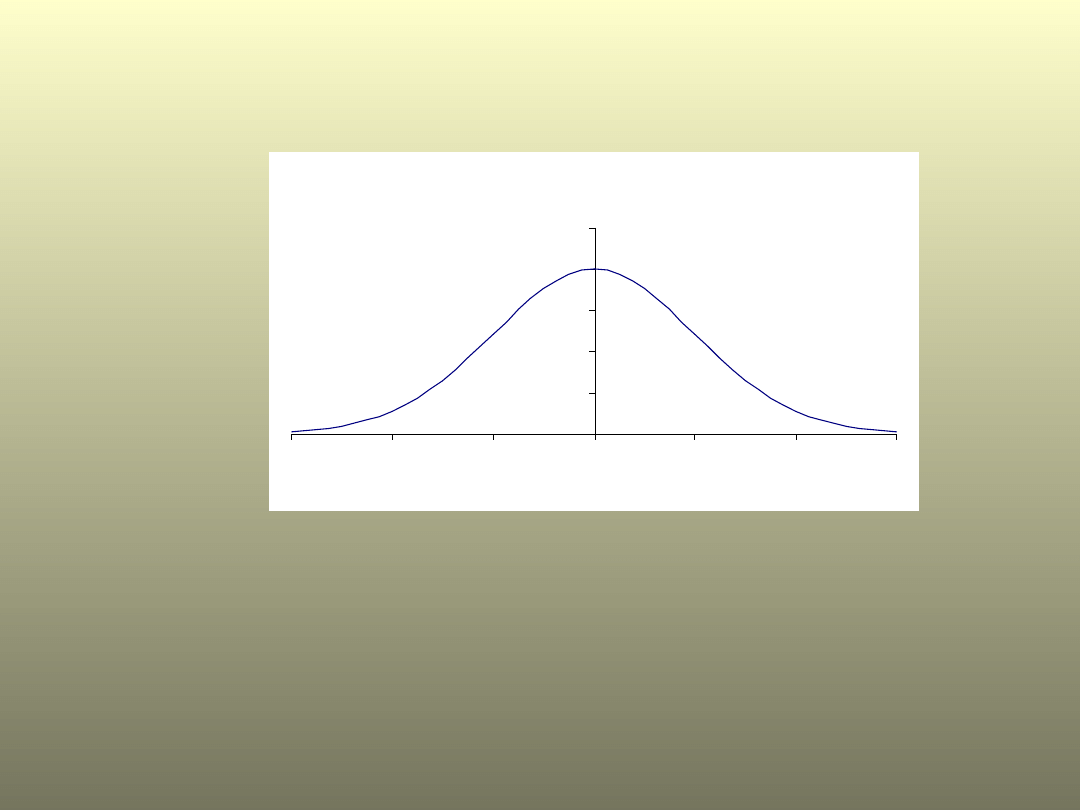
Rozkład normalny
W statystyce istnieje wiele rozkładów

teoretycznych. Najczęściej
występującym to rozkład normalny:

P(-<x<)=1

Rozkład normalny określony przez
funkcję gęstości:

2

2

2

)

(

2

1

)

(





















x

e

x

f

gdzie:
e,  - stałe matematyczne
 - średnia w populacji;
 - odchylenie standardowe w populacji

Zmienna losowa ma rozkład normalny o
parametrach



,



, co piszemy N(



,



).

Parametr



wyznacza środek symetrii

wykresu, a parametr



decyduje o jego

wysokości

Estymatory punktowe

średniej



szereg
szczegółowy







n

i

i

x

n

x

1

1

szereg rozdzielczy punktowy







k

i

i

i

n

x

n

x

1

1

szereg rozdzielczy

o

przedziałach

klasowych







k

i

i

i

n

x

n

x

1

1



Metody wnioskowania

statystycznego

• Estymacja punktowa
• Estymacja przedziałowa
• Weryfikacja hipotez statystycznych

Estymować inaczej oceniać pewne rozkłady, czy

parametry rozkładów

Weryfikować inaczej sprawdzać

założenia/przypuszczenia nazywane dalej
hipotezami

Wnioskowanie
statystyczne

Prawdopodobieństwo

• A – zdarzenie losowe
• P(A) – prawdopodobieństwo zdarzenia

losowego jest to funkcja zdarzeń losowych
przyjmująca wartości rzeczywiste i
spełniająca następujące warunki:

• (*) 0 < P(A) <1
• (**) dla A i B rozłącznych;

P(A lub B) = P(A) + P(B)

• (***) P( zdarzenia niemożliwego) = 0

Własności

prawdopodobieństwa

• 1) P( zdarzenia pewnego) = 1
• 2) P(A lub B) = P(A) + P(B – P(A i B)
• 3) jeżeli zd.A zawiera się w B,

to P(A) < P(B)

4) jeśli A’ jest zdarzeniem

przeciwnym do zdarzenia A, to P
( A’) = 1- P(A)

Zmienna losowa

• Zmienną losową nazywamy każdą funkcje

zdarzeń losowych przyjmującą wartości

rzeczywiste.

• Podobnie jak badane cechy zmienną losową

dzielimy na skokową (dyskretną) i ciągłą.

• Przykładami zmiennej losowej skokowej są:
• liczba szczepień, liczba chorych, tętno.
• Przykładami zmiennej losowej ciągłej są:

temperatura, ciśnienie tętnicze krwi

Parametry

opisowe

zbiorowoś

ci

statystycz

nej

charakterystyki

liczbowe, dające

sumaryczny i

skrócony opis

zbiorowości

statystycznej.

Rozkład zmiennej losowej

Zmienne

losowe i

ich

rozkłady

charakterystyki

liczbowe, dające opis

zbiorowości

statystycznej pod

względem częstości

występowania

wartości zmiennej

losowej.

Jeżeli na n osób m jest liczbą kobiet, to możemy
powiedzieć, że prawdopodobieństwo że x jest
kobietą, co zapiszemy P(x=kobieta) wynosi
m/n; 0<=P<=1

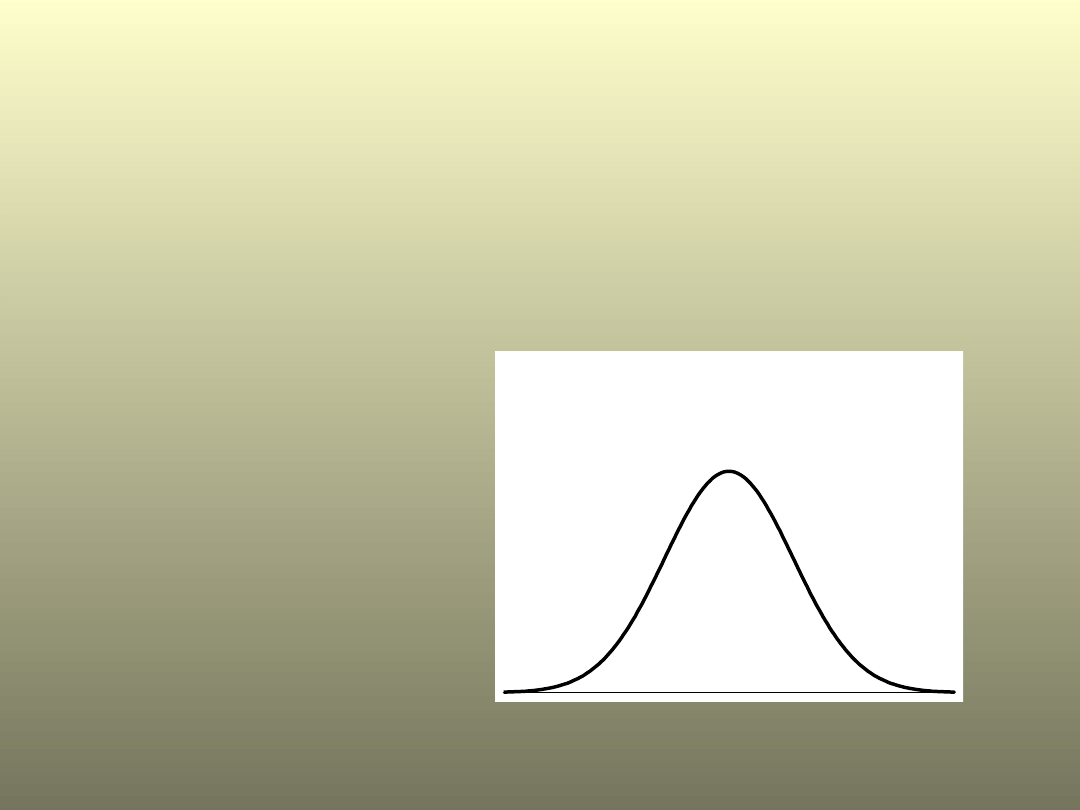
Rozkład normalny
W statystyce istnieje wiele rozkładów

teoretycznych. Najczęściej
występującym to rozkład normalny:

P(-<x<)=1

Rozkład normalny określony przez
funkcję gęstości:

2

2

2

)

(

2

1

)

(





















x

e

x

f

gdzie:
e,  - stałe matematyczne
 - średnia w populacji;
 - odchylenie standardowe w populacji

Zmienna losowa ma rozkład normalny o
parametrach



,



, co piszemy N(



,



).

Parametr



wyznacza środek symetrii

wykresu, a parametr



decyduje o jego

wysokości

Przedział ufności

Reguła 3 sigm



)

(x

f

f(x)

0,0

0,1

0,2

0,3

0,4

0,5

-3

-2

-1

0

1

2

3

x

Wykres funkcji gęstości rozkładu normalnego dla =0

i =1

Jeżeli zmienna losowa X ma rozkład normalny N(



,σ) to:

P(



- σ<x<



+ σ) =0, 6827 - 68,27 % wyników jest w przedziale (



-σ,



+ σ)

P(



-2σ<x<



+2σ) =0, 9545 - 95,45 % wyników jest w przedziale (



-2σ,



+2σ)

P(



- 3σ<x<



+ 3σ) =0, 9973 - 99,73 % wyników jest w przedziale (



-3σ,



+ 3σ)

Estymatory punktowe

przedziałowe średniej

populacji



szereg
szczegółowy







n

i

i

x

n

x

1

1

szereg rozdzielczy punktowy







k

i

i

i

n

x

n

x

1

1

szereg rozdzielczy

o

przedziałach

klasowych







k

i

i

i

n

x

n

x

1

1



 

P

rzykład

Zmierzono wzrost 100 siedmioletnich dzieci.
Obliczona średnia x=35 cm i odchylenie

standardowe s=5 cm.
Przy założeniu że cecha ta ma rozkład normalny i
korzystając z prawa „trzech sigm” można wyliczyć
odpowiednie przedziały:

P(35-5<x< 35+5) =0, 6827  68,27 % wyników

jest w przedziale (30, 40),
P(35-10<x< 35+10) =0, 9545  95,45 % wyników

jest w przedziale (25, 45),
P(35-15<x< 35+15) =0, 9973  99,73 % wyników

jest w przedziale (20, 50).

Wiele metod statystycznych stosowanych do
analizy danych wymaga założeń normalności
rozkładu badanej cechy.
 

ZADANIA PARAMETRÓW

OPISOWYCH

Określenie:
• przeciętnego poziomu zmiennych opisujących

analizowane cechy statystyczne przez wybór

pojedynczej wartości, tj. miary przeciętnej

(położenia), reprezentującej wszystkie

wartości szeregu,

• zmienności (dyspersji, rozproszenia) wartości

zmiennych w obserwowanej zbiorowości,

• miary asymetrii tj. w jakim stopniu badany

szereg odbiega od idealnej symetrii,

• miary koncentracji tj. stopnia skupienia

poszczególnych jednostek wokół średniej.

PODSTAWOWE RÓŻNICE

MIĘDZY ZBIOROWOŚCIAMI

• Rozkłady mogą się różnić:
• położeniem, tzn. wartością zmiennej,

w pobliżu której skupiają się obserwacje,

• obserwacje mogą się skupiać wokół tej

samej wartości, lecz różnić obszarem
zmienności,

• rozkłady mogą różnić się jednocześnie

co do obu tych charakterystyk
liczbowych.

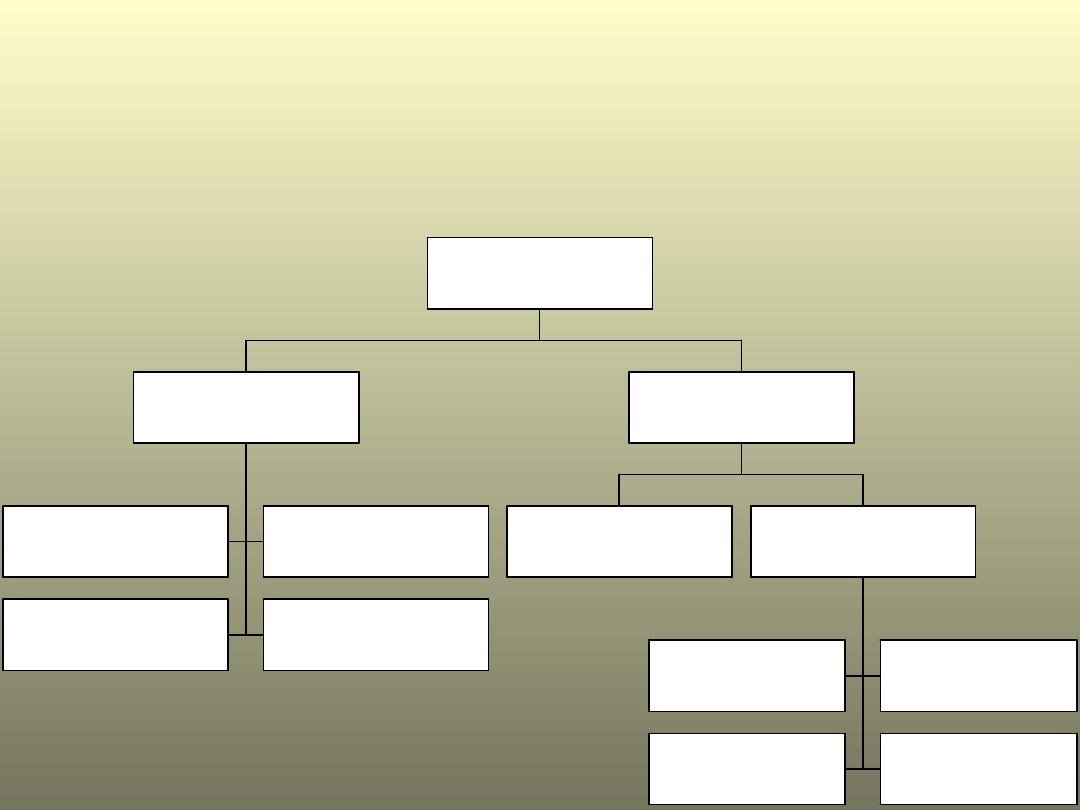
KLASYFIKACJA MIAR

ŚREDNICH

ś re d n ia a ry tm e ty c z n a

ś re d n ia h a rm o n ic z n a

ś re d n ia g e o m e try c z n a

ś re d n ia k w a d ra to w a

k la s y c z n e

d o m in a n ta , m o d a ln a

k w a rty le z m e d ia n ą

k w in ty le

d e c y le

c e n tyle

k w a n ty le

p o z yc y jn e

m ia ry ś re d n ie

• Dobór odpowiednich testów

statystycznych

• Przykłady obliczeń w STATISTICA:

test t Studenta i analiza wariancji
test chi-kwadrat
testy nieparametryczne
korelacja i regresja

Analiza danych oparta o

weryfikację hipotez statystycznych

Weryfikacja i testy statystyczne

• H0: hipoteza zerowa (1= 2)

• H1: hipoteza alternatywna (1 2,)

• W oparciu o wynik obliczonego testu z

danych z próby możemy H0: odrzucić lub

nie.

• Nie wiemy czy H0: zachodzi w populacji.

• Zatem można popełnić:

• błąd I rodzaju jeśli odrzucimy H0 jeśli

jest prawdziwa w populacji

• błąd II rodzaju jeśli nie odrzucimy H0

wtedy kiedy jest ona fałszywa w populacji

• W naukach medycznych przyjmujemy

poziom istotności  = 0,05

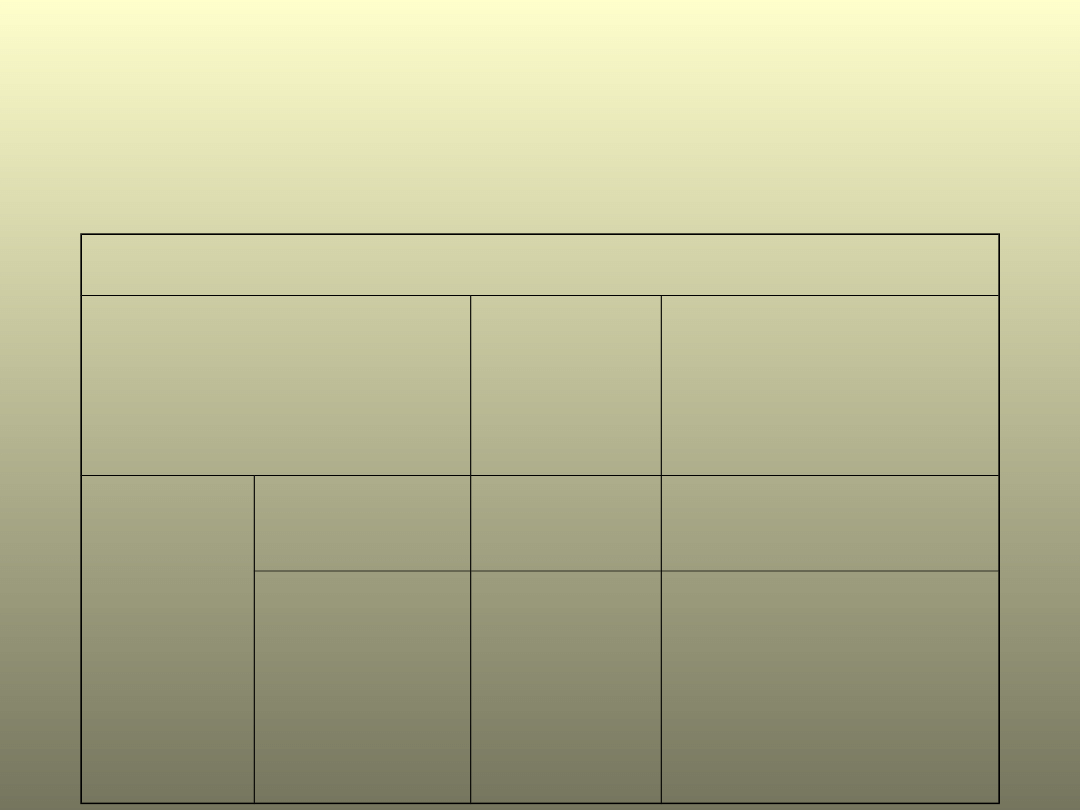
Błędy przy wnioskowaniu

 = prawdopodobieństwo popełnienia

błędu I rodzaju

= prawdopodobieństwo popełnienia błędu

II rodzaju

Populacja

H

0

jest

prawdziw

a

H

0

jest fałszywa

Czyli prawdziwa

jest

H

1

Decyzj
a z
wynikó
w
oblicze
ń

z

próby

Przyjęcie

H

0

1- 

Błąd II rodzaju



Odrzucenie

H

0

Błąd I

rodzaju



1- 

Sformułować hipotezę zerową H

o

i alternatywną

H

1

oraz dobrać odpowiedni test do weryfikacji

Wykonać obliczenia i wybrać potrzebne

wyniki, przede wszystkim wartość p określającą

prawdopodobieństwo

popełnienia

błędu

odrzucenia H

o

, gdy jest prawdziwa w populacji

(błąd I rodzaju).

Przyjąć poziom istotności , ale mniejszy niż

lub równy 0,05.

Podjąć decyzję o hipotezie zerowej H

o

:

jeżeli obliczona wartość p ≤ , odrzucamy H

o

i

przyjmujemy H

1

jeżeli obliczona wartość p > , to brak podstaw

do odrzucenia H

o

.

• Wniosek w populacji z obliczeń w grupie

.

Schemat weryfikacji

hipotez

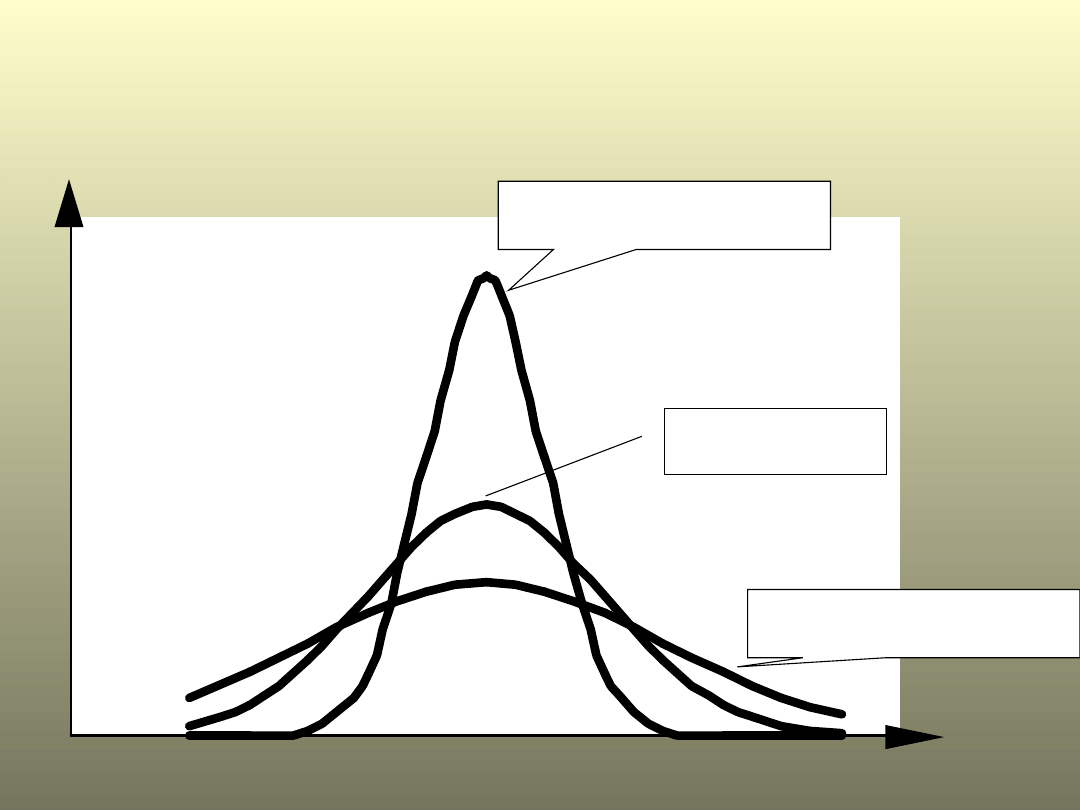
Test t-Studenta

Założenie:

Cecha X ma rozkład normalny w obu

populacjach o jednorodnych wariancjach, czyli N(



1

,

)

i

N(



2

,

)

leptokurtyczny

platokurtyczny

normalny

n

i

x

i

Test t-Studenta dla dwóch średnich

• H0: 1= 2 hipoteza zerowa

• H1: 1 2, hipoteza alternatywna

• Gdzie

• dane, średnie i liczebności w próbach

• W pakiecie statystycznym wyliczamy t i wartość p równą

prawdopodobieństwu popełnienia błędu I rodzaju

(odrzucenie prawdziwej H0 )

• Wartość p porównujemy z przyjętym poziomem istotności 

• Jeżeli p<  odrzucamy H0 i stwierdzamy istotną różnicę

między średnimi

• Przykłady w STATISTICA

)

1

1

(

2

)

(

)

(

2

1

2

1

2

2

2

2

1

1

2

1

n

n

n

n

x

x

x

x

x

x

t

i

i





















j

j

ij

n

x

x

,

,

Przykład

H0: średni wzrost mężczyzn= średni

wzrost kobiet w populacji

H0: średni wzrost mężczyzn średni

wzrost kobiet w populacji

n Średnia Odch.std. n Średnia Odch.std.

WZROST (m) 65 1,72

0,05 81 1,67

0,05 6,25 0,000 1,22 0,40

Cecha

Równość średnich

jednorodność

wariancji

Mężczyźni

Kobiety

t

p iloraz F p

Analiza wariancji

-

kilka populacji

• Dodatkowym założeniem które powinno być

spełnione to jednorodność wariancji. Należy

więc zweryfikować hipotezę zerową Ho:

21=. . . =2k kontra alternatywnej H1:

wariancje są niejednorodne (test Levene’a)

• ANOVA

• Hipoteza zerowa Ho: 1=. . . =k

• H1: średnie są różne pomiędzy sobą.

• Jeżeli stwierdza się istotność różnic pomiędzy

średnimi, to należy znaleźć pomiędzy którymi

średnimi te różnice są istotne (test Scheffego)

Tablica z wynikami analizy

wariancji

Ź

r

ó

d

ł

o

S

u

m

a

k

w

a

d

r

a

t

ó

w

S

t

o

p

n

i

e

s

w

o

b

o

d

y

Ś

r

e

d

n

i

a

k

w

a

d

r

a

t

ó

w

W

a

r

t

o

ś

ć

F

(

W

a

r

t

o

ś

ć

p

)

Z

m

i

e

n

n

o

ś

ć

m

i

ę

d

z

y

g

r

u

p

o

w

a

S

S

m

k

-

1

V

m

=

1

m

S

S

k



m

b

V

F

V



B

ł

ą

d

S

S

b

n

-

k

V

b

=

b

S

S

nk



G d z ie: k – lic z b a g r u p ; n – lic z b a w sz y stk ic h o só b z e w sz y stk ic h g r u p

2

2

1

1

1

(

) ;

(

)

j

n

k

k

m

j

j

b

i j

j

j

j

i

S S

n

x

x

S S

x

x

















 

x

ij

w y n ik c e c h y u i- tej o so b y w j- tej g r u p ie , n

j

– lic z b a o só b w j- te j g r u p ie

 x

j

– śr e d n ia w j - tej g r u p ie ,  x – śr e d n ia z w sz y stk ic h p o m ia r ó w

Jeżeli wartość p <0,05 to są różnice między średnimi, należy

znaleźć między którymi (test Scheffe’go)

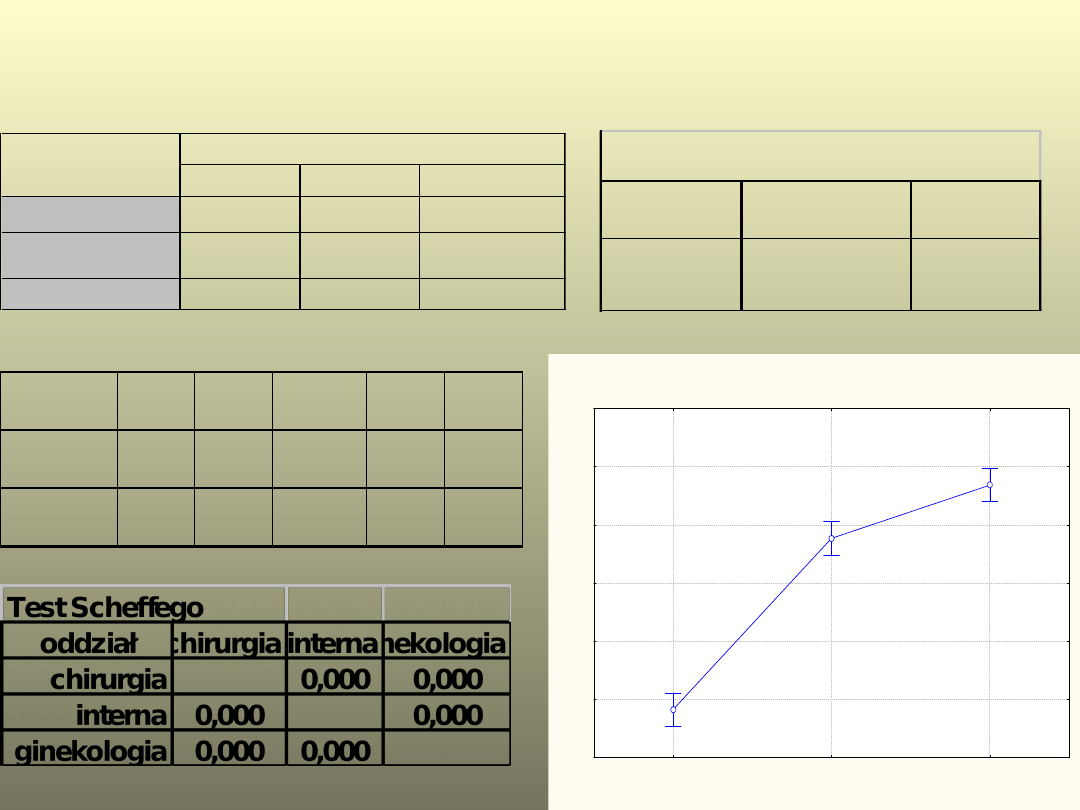
Przykład ANOVA

n



x

s

chirurgia

21

39,1

2,8

interna

21

53,9

3,4

ginekologia

21

58,4

3,6

oddział

wiek

Test Levene'a

F

p

wiek

1,61

0,21

Źródło

SS Stopnie V

F

p

oddział

4265,4

2 2132,7 198,00 0,00

Błąd

646,3

60

10,8

Bieżący efekt: F(2, 60)=198,00, p=0,0000

Pionowe słupki oznaczają 0,95 przedziały ufności

chirurgia

interna

ginekologia

oddział

35

40

45

50

55

60

65

w

ie

k

Test Manna-Whitneya

• Stosowany do oceny różnic jednej cechy pomiędzy dwoma

populacjami, gdy nie spełnione założenia przy teście t_Studenta

Dane: x

11

, . . . x

n1

z 1-szej populacji; x

12

, . . . x

m2

z 2-giej populacji.

Porządkujemy obie próby razem i nadajemy im rangi oddzielnie.

Wartość tego testu wyliczana jest z wzoru:

1

(

1)

2

n n

U nm

R









gdzie: n, m liczebności grup, R

1

jest sumą rang w 1-szej grupie.

Jeżeli p<  stwierdzamy istotną różnicę

analizowanej cechy między populacjami

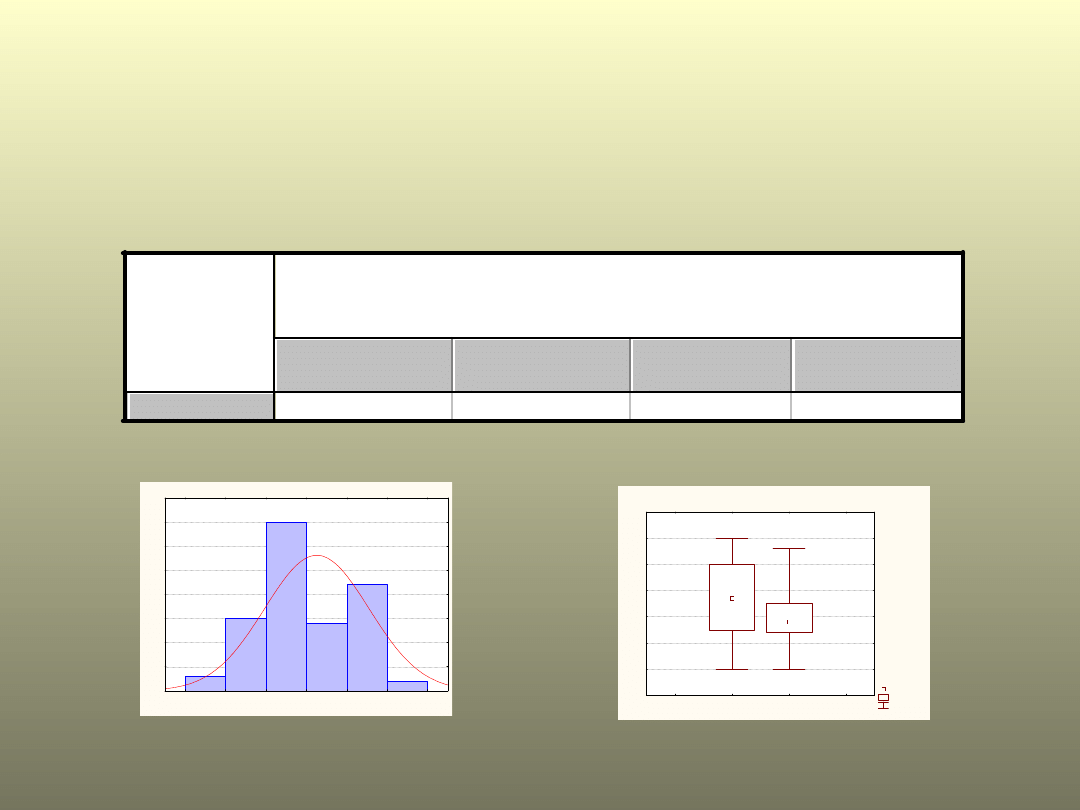
Przykład

U kobiet tętno w

cukrzycy

T

est U Manna-Whitneya (bazaStomat)

Wzg.zmienn. Cukrzyca

zmienna

Sum.rang

NIE

Sum.rang

TAK

U poziom p

Tętno

2470

1717

771

0,038

Histogram: Tętno

50

60

70

80

90

100

110

X <= Granica klasy

0

5

10

15

20

25

30

35

40

Li

cz

b

a

o

b

s.

Wykres ramka-wąsy dla grup

Zmienna: Tętno

Mediana
25%-75%
Min.-Maks.

NIE

TAK

Cukrzyca

50

60

70

80

90

100

110

120

Tę

tn

o

Test Chi2

Dane w tabeli czteropolowej:

X

Cechy

1

0

1

a

b

Y

0

c

d

H

0

: cechy X, Y są niezależne

H

1

: cechy X, Y są zależne

C

h

i

2

=

2

(

)(

)

( )( )( )( )

a

db

cabcd

acbdabcd





   

Jeżeli wartość p <0,05 to cechy X, Y są zależne

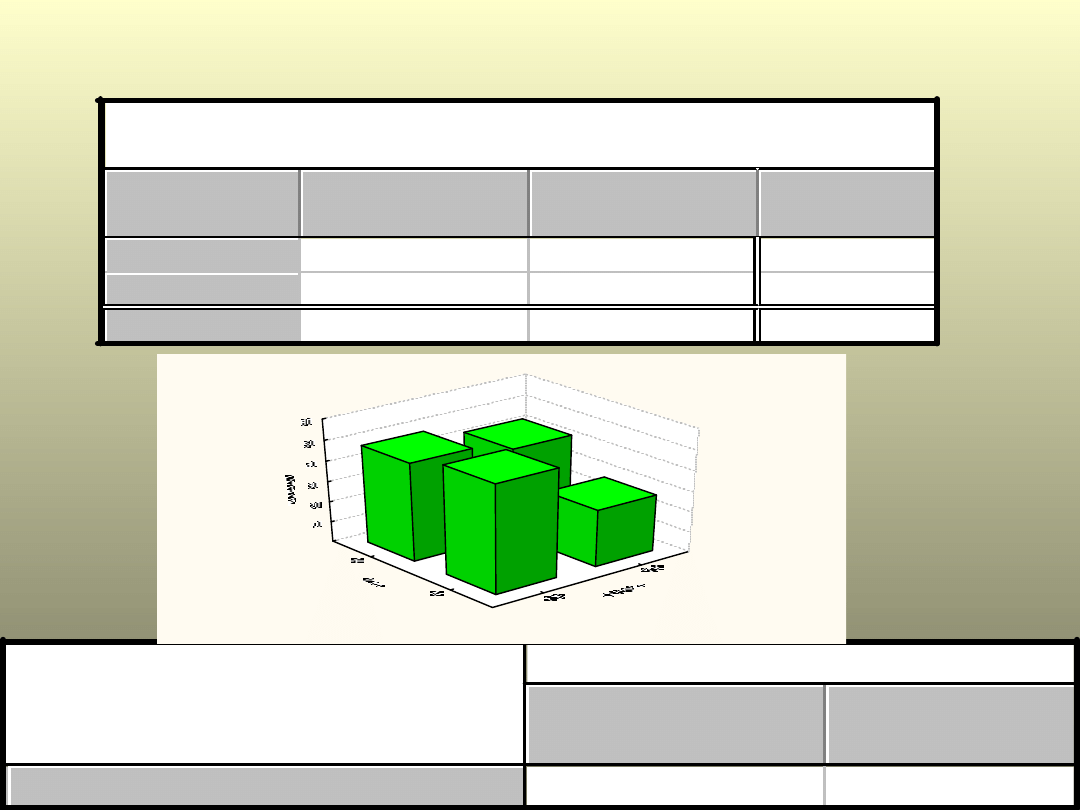
Przykład.Cukrzyca i

płeć

T

abela liczności (bazaStomat)

T

abela:Płeć(2) x Cukrzyca(2)

Płeć

Cukrzyca

NIE

Cukrzyca

TAK

Wiersz

Razem

M

53

28

81

K

48

43

91

Ogół grp

101

71 172

Płeć x Cukrzyca

Statystyki:

Chi-kwadr

.

p

Chi kwadrat Pearso

2,844759

p=,09168

Roz kład dwuwymiarowy: Płeć x Cukrz yca

Korelacja prostoliniowa

Pearsona

H

0

: cechy X, Y są niezależne

H

1

: cechy X, Y są zależne

Dane: x

1

, . . . x

n

wyniki 1-szej cechy; y

1

, . . . y

n

2-giej cechy

w n-elementowej próbie.

W

a

r

t

o

ś

ć

w

s

p

ó

ł

c

z

y

n

n

i

k

a

1

2

2

1

1

(

)

(

)

(

)

(

)

n

i

i

i

n

n

j

j

i

i

x xy y

r

x x

y y























Jeżeli wartość p <0,05 to cechy X, Y są zależne

Regresja logistyczna

• W naukach medycznych mamy często

sytuacje, gdy zmienna zależna jest typu
dychotomicznego. Przykładowo może to być
cecha występowanie choroby z poziomami:
1 - tak, 2 - nie.

• Szukamy wówczas powiązania, podobnego

do funkcji regresji, pomiędzy
prawdopodobieństwem wystąpienia choroby
grupą zmiennych niezależnych, takich jak
np: wiek, płeć lub nawyki palenia.

Regresja prostoliniowa

y=ax+b

Dane: x

1

, . . . x

n

wyniki 1-szej cechy; y

1

, . . . y

n

2-giej cechy

w n-elementowej próbie.

1

2

1

;

(

)(

)

(

)

n

i

i

i

n

j

i

x x y y

a

b y ax

x x











 







• Współczynniki regresji a i b liczymy wtedy jeżeli x i

y są skorelowane

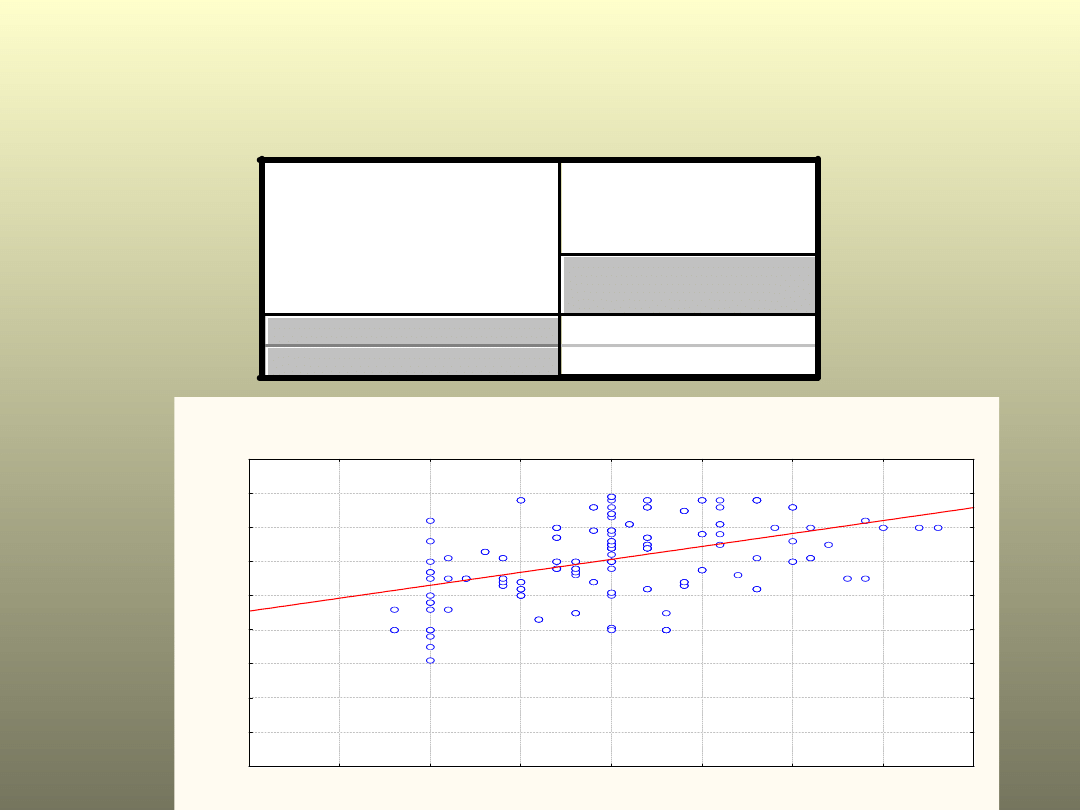
Przykład: waga i wzrost

Korelacje

Zmienna

WAGA (kg)

WZROST (m)

r=0,4340

p=,000

WZROST (m) vs. WAGA (kg)

WAGA (kg) = -48,32 + 75,884 * WZROST (m)

Korelacja: r = ,43400

1,50

1,55

1,60

1,65

1,70

1,75

1,80

1,85

1,90

WZ ROST (m)

20

30

40

50

60

70

80

90

100

110

W

A

G

A

(

k

g

)

Regresja logistyczna

• W naukach medycznych mamy często

sytuacje, gdy zmienna zależna jest typu
dychotomicznego. Przykładowo może to być
cecha występowanie choroby z poziomami:
1 - tak, 2 - nie.

• Szukamy wówczas powiązania, podobnego

do funkcji regresji, pomiędzy
prawdopodobieństwem wystąpienia choroby
grupą zmiennych niezależnych, takich jak
np: wiek, płeć lub nawyki palenia.

Tabela

Narażenie

Nowotwór płuc

wystąpił

nie wystąpił

Palący

243

30

Niepalący

48

240

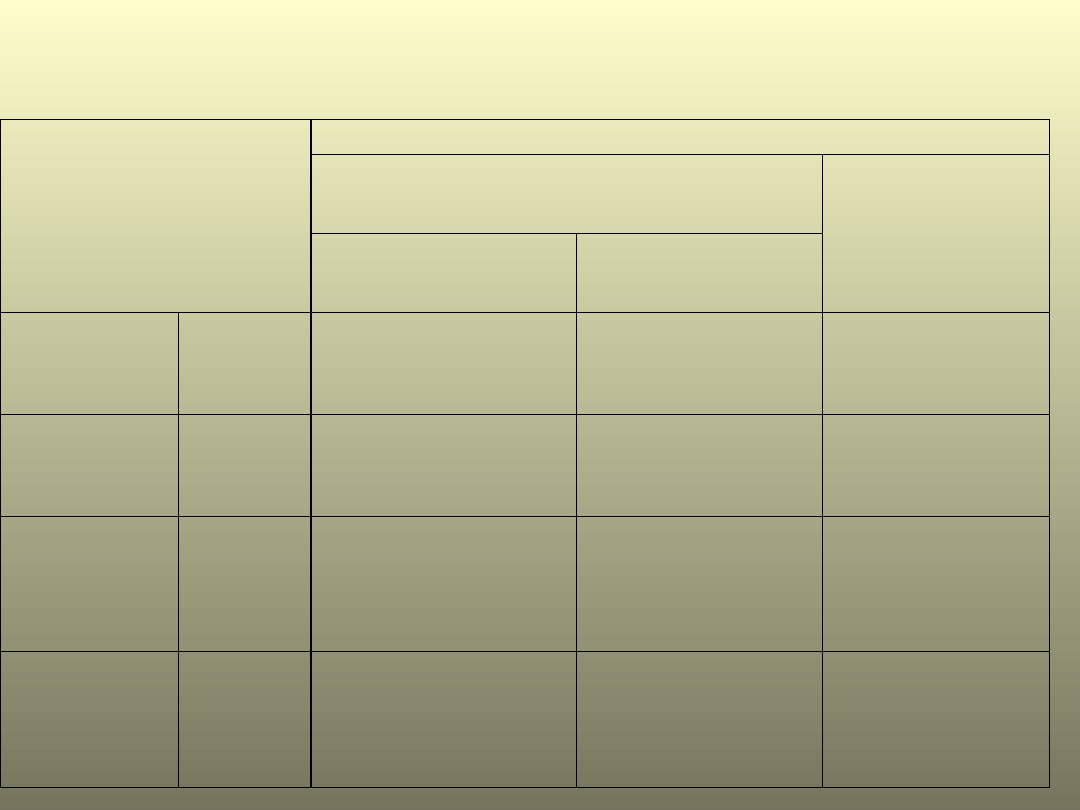
Propozycja doboru testu statystycznego w zależności

od rodzaju cechy i typu analizy

Rodzaj cechy

Ilościowa

Spełnione założenia stosowania testu

parametrycznego

Typ analizy

Tak

Testy parametryczne

Nie

Testy

nieparametryczne

Jakościowa

1 cecha

2

grupy

Test t-Studenta

dla prób

niezależnych

Test Manna-

Whitney’a

Wilcoxona

Test



2

1 cecha

Więcej

niż 2

grupy

Analiza

wariancji

ANOVA

Test

Kruskala-

Wallisa

Test



2

1 cecha

mierzona

2 razy

1

grupa

Test t-Studenta

dla prób

zależnych

Test rang

Wilcoxona

dla prób

zależnych

Test 

2

lub test McNemary

2 cechy

1

grupa

Współczynnik

korelacji

prostoliniowej

Pearsona

Współczynnik

korelacji rang

Spearmana

Test



2

i współczynniki

siły związku