POLITECHNIKA ŚWIĘTOKRZYSKA

ZAKŁAD BADAŃ OPERACYJNYCH I SYSTEMÓW STEROWANIA

LABORATORIUM TEORII STEROWANIA I SYSTEMÓW

INSTRUKCJA

ĆWICZENIE LABORATORYJNE NR 2

Temat:

SERWOMECHANIZM

KIELCE 1999

CEL ĆWICZENIA

Zapoznanie się z układem serwomechanizmu prądu stałego oraz z wpływem jego parametrów na własności dynamiczne oraz statyczne.

1. POJĘCIA PODSTAWOWE

Wiele spotykanych w technice procesów ma strukturę pokazaną na rys. 1. Występuje więc układ, który badamy lub zamierzamy wpływać na jego zachowanie nazywamy obiektem sterowanym; sygnały wejściowe obiektu są sygnałami sterującymi, wyjściowe - sygnałami sterowanymi. Oddziaływanie na obiekt zmierzające do wywołania określonego efektu nazywamy sterowaniem. Zamierzone zachowanie się obiektu jest celem sterowania. Dla realizacji celu należy doprowadzić do wejścia obiektu odpowiedni sygnał. Sygnał ten jest kształtowany przez urządzenie sterujące. Urządzenie sterujące i obiekt sterowany tworzą układ sterowania. Zazwyczaj występują też zakłócenia - sygnały utrudniające realizację celu sterowania. Jeśli do wytworzenia sygnału sterującego wykorzystywana jest na bieżąco informacja o sygnale sterowanym, to mówimy o sterowaniu w układzie zamkniętym lub o układzie regulacji; jeśli tak nie jest, to mówimy o otwartym układzie sterowania. Struktura podana na rys. 1 nosi nazwę układu regulacji.

W automatyce dużą grupę stanowią układy regulacji nadążnej położenia, zwane serwomechanizmami. Sygnałem wejściowym jest więc w nich przesunięcie liniowe lub kątowe. Zadaniem serwomechanizmów jest odtwarzanie z dużą dokładnością ruchów zadawanych przez układy czujników małej mocy.

Przykładem serwomechanizmu może być układ napędu pisaka w rejestratorze (autokompresorze), który ustawia pisak w położeniu proporcjonalnym do wartości sygnału doprowadzonego na wejście. Serwomechanizmem jest też urządzenie sterujące frezarką kopiującą, w którym położenie freza odtwarza położenie czujnika odczytującego kształt szablonu.

Innymi przykładami mogą być: układ stabilizacji położenia wieżyczki czołgu podczas jazdy w nierównym terenie lub radiolokacyjny układ śledzenia za poruszającym się celem. We wszystkich omawianych przypadkach odtwarzanie położenia odbywa się w układzie regulacji, tzn. przez porównanie sygnału proporcjonalnego do położenia, pochodzącego z czujnika wartości zadanej y₀ z położeniem elementu nastawiającego y i oddziaływanie na niego w zależności od sygnału różnicy ε= y₀ - y zwanej uchybem regulacji. Wyodrębnienie serwomechanizmów spośród układów regulacji wynika ze szczególnie ostrych wymagań dokładności; ponadto możliwość wystąpienia dużych sygnałów zadanych lub zakłócających wymaga szczegółowej analizy wpływu nieliniowości elementów serwomechanizmu.

2. ANALIZA WŁASNOŚCI SERWOMECHANIZMU LINIOWEGO

1. Zasada działania serwomechanizmu

Schemat typowego serwomechanizmu jest przedstawiony na rys. 2. Obiekt O, którym może być przykładowo element piszący rejestratora, jest wprawiany w ruch za pośrednictwem silnika S poprzez przekładnię I. Z obiektem sprzężony jest suwak potencjometru P - w ten sposób uzyskuje się sygnał elektryczny v_y wprost proporcjonalny do położenia obiektu y. Żądane położenie obiektu y₀ (sygnał zadany) może ustawić suwakiem potencjometru P₀ - uzyskuje się napięcie v_y0 wprost proporcjonalne do y₀. Uchybowi regulacji ε = y₀ - y odpowiada różnica napięć v_ε = v_y0 - v_y. Napięcie uchybu v_εjest wzmacniane; napięcie wyjściowe wzmacniacza v_m steruje od strony wirnika silnik prądu stałego S o stałym prądzie wzbudzenia i_w. Silnik S napędza przez przekładnię I obiekt O i suwak potencjometru P tak, aby zmniejszyć napięcia uchybu. Zatem sprzężenie zwrotne w tym układzie regulacji jest ujemne. Ruch silnika trwa tak długo, dopóki uchyb nie zmaleje do zera. W celu poprawienia własności dynamicznych serwomechanizmu wprowadza się dodatkowe ujemne sprzężenie zwrotne proporcjonalne do
lub
(gdzie α - kąt obrotu wału silnika). Odpowiedni sygnał elektryczny uzyskuje się z prądnicy - zwanej tachometryczną - sprzężonej z wałem silnika (prądnica Pr na rys. 2). Często silniki wykonawcze serwomechanizmów - serwomotory - i prądnice tachometryczne tworzą jedną konstrukcję mechaniczną. Rola sprzężenia prędkościowego (tachometrycznego będzie omówiona w dalszych punktach.

2.2. Równania prostego serwomechanizmu

Rozważmy układ z rysunku 2.

Napięcia i położenia potencjometrów związane są zależnościami:

v_y0 = k_py₀, v_y = k_py,

zaś uchyb ε i napięcie v_ε zależnością

v_ε= v_y0 - v_y = k_p(y₀ - y) = k_pε.

Zakładając, że pasma częstotliwości przenoszonych sygnałów są szersze dla wzmacniaczy niż dla silnika, można traktować wzmacniacze jako człony proporcjonalne o współczynnikach wzmocnienia odpowiednio k i k₀. Zatem

v = kv_ε oraz v_m = k₀(v - v_t),

przy czym v_t=
reprezentuje sygnał tachometrycznego sprzężenia zwrotnego. Współczynnik k_t uwzględnia stałą prądnicy tachometrycznej i dzielnik napięcia.

Równanie silnika można uzyskać pamiętając, że w każdej chwili moment hamujący (iloczyn momentu bezwładności sprowadzonego do wału silnika J i przyspieszenia
) oraz moment napędowy są sobie równe

,

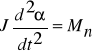
gdzie M_n - moment napędowy.

Zakładamy przy tym, że wartości innych momentów (np. momentu pochodzącego od siły tarcia) są do pominięcia. Moment napędowy silnika przy stałym prądzie wzbudzenia i_w (a więc dla stałego strumienia magnetycznego stojana) jest proporcjonalny do prądu wirnika i_m

M_n = k_mi_m

gdzie k_m - współczynnik proporcjonalności.

Przy pominięciu indukcyjności wirnika można obliczyć prąd i_m, znając rezystancję R_m wirnika, jako

i_m=

Wielkość e_m jest siłą przeciwelektromotoryczną indukowaną w wirniku, powstającą w wyniku ruchu uzwojeń wirnika w polu stojana. Siła przeciwelektromotoryczna jest zatem wprost proporcjonalna do prędkości kątowej wirnika

e_m=

Uwzględniając powyższe zależności, można otrzymać równanie różniczkowe opisujące dynamikę silnika sterowanego napięciem wirnika

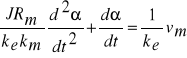
Po dokonaniu przekształcenia Laplace'a otrzymujemy związek

Jest to transmitancja silnika, przy czym k₁=
, T=
. Parametr T jest nazywany stałą czasową silnika. Silnik sterowany napięciem wirnika można zatem przedstawić jako połączenie członu całkującego (
) i inercyjnego (
).

Z kolei transmitancja członu sprzężenia tachometrycznego ma postać

Zakładając, że przekładnica mechaniczna jest bezluzowa i ma przełożenie I, można napisać następujący związek między kątem obrotu silnika α i położeniem obiektu y

y(s) = Iα(s)

Na rys. 3a przedstawiony jest schemat strukturalny serwomechanizmu pokazujący sposób powiązania poszczególnych elementów, ich właściwości (w postaci transmitancji wpisanych do prostokątów symbolizujących elementy) oraz sygnały pośredniczące. Miejsca oznaczone kółkami, do których doprowadzone są sygnały z odpowiednimi znakami, nazywane są węzłami sumującymi.

Właściwości dynamiczne serwomechanizmu - takie cechy jak stabilność, parametry odpowiedzi skokowej, parametry odpowiedzi na sygnał liniowo narastający, sinusoidalny itp. - można w łatwy sposób ocenić, analizując transmitancje układu. Podstawowe znaczenie ma tu rozkład biegunów transmitancji układu zamkniętego. W dalszych rozważaniach zamiast parametrów konstrukcyjnych będziemy operować zastępczymi parametrami obliczeniowymi serwomechanizmu. Podejście to pokrywa się z podejściem użytkownika serwomechanizmu, którego nie muszą interesować parametry konstrukcyjne, chyba że jest możliwe nastawienie w pewnym zakresie ich wartości. Zastępczymi parametrami serwomechanizmu (bez sprzężenia tachometrycznego) są stała czasowa T oraz współczynnik wzmocnienia prędkościowego k_v = k k_v' gdzie k_v'=
. Odpowiada to przyjęciu do dalszych rozważań schematu serwomechanizmu z rys. 3b (można przyjąć jednostkowe współczynniki k_p oraz I).

Związek między transformatami sygnałów y i ε można teraz napisać jako y(s)= G₀(s) ε(s)

G₀(s)=

jest to transmitancja układu otwartego.

W praktyce współczynnik k_v oraz stałą czasową T danego serwomechanizmu można określić badając właściwości dynamiczne jego układu otwartego, tzn. wyznaczając charakterystyki częstotliwościowe lub czasowe w tym układzie.

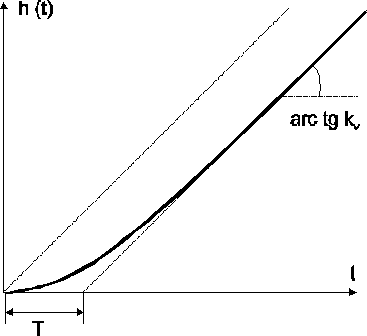
Charakterystyka skokowa h(t) układu o transmitancji G₀(s) jak wyżej, a więc przebieg y(t) przy sygnale ε(t) = 1(t) na wejściu, jest przedstawiona na rys. 4.

Z odpowiedzi tej można obliczyć k_v jako nachylenie przebiegu
(prędkość), przy t → ∝ oraz T jako odcinek na osi odciętych między t = 0 a przecięciem z asymptotą przebiegu h(t) dla
t → ∝. Niekiedy można rejestrować pochodną charakterystyki skokowej, a więc przebieg prędkości sygnału wyjściowego (rys. 5); otrzymujemy wtedy charakterystykę impulsową k(t) (odpowiedź na sygnał δ(t)). Z przebiegu tego można również określić wartości k_v oraz T w sposób pokazany na rysunku. Należy tu dodać, że wzmocnienie prędkościowe k_v jest parametrem charakterystycznym każdego członu całkującego i może być interpretowane jako prędkość zmiany sygnału wyjściowego tego członu po doprowadzeniu na jego wejście skoku jednostkowego. Istnieje możliwość wyznaczenia parametrów k_v i T charakterystyki częstotliwościowej układu otwartego. W tym celu najlepiej jest wykreślać charakterystyki we współrzędnych logarytmicznych (charakterystyki Bodego).

Związek między 0transformatami sygnałów y i y₀ dla badanego serwomechanizmu, zwany transmitancją układu zamkniętego, ma postać

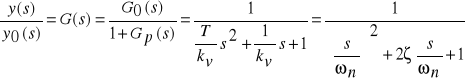
i odpowiada transmitancji układu oscylacyjnego o częstotliwości drgań własnych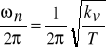
i współczynniku tłumienia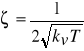
. charakterystyki skokowe h(t) tego członu są pokazane na rys. 6. Częstotliwość drgań własnych
nie ma przy tym wpływu na charakter przebiegu h(t), a jedynie na jego rozciągnięcie wzdłuż osi czasu. O charakterze przebiegu decyduje wartość współczynnika tłumienia ζ. Jedynie dla ζ<1 rozpatrywany układ jest oscylacyjny w sensie ścisłym; dla ζ≥1 staje się on członem inercyjnym drugiego rzędu - układ ma dwa bieguny rzeczywiste. Przy ζ= 0,707 oscylacje są praktycznie niewidoczne i używa się w odniesieniu do układu oraz jego odpowiedzi skokowej określenia “aperiodyczny krytyczny”.

Rozpatrzymy teraz układ ze sprzężeniem tachometrycznym.

Jak widać ze schematu uproszczonego z rys. 3b, sprzężenie tachometryczne obejmuje tylko część układu otwartego o wzmocnieniu (prędkościowym) k_v zaś pozostała część (współczynnik wzmocnienia k) znajduje się “poza pętlą”

sprzężenia tachometrycznego. Spodziewamy się zatem, że współczynnik k będzie oddziaływał niezależnie od wpływu współczynnika k_t. Rzeczywiście, przekształcenie układu przez wyeliminowanie wewnętrznej pętli sprzężenia zwrotnego prowadzi do nowej transmitancji układu otwartego

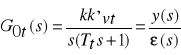
gdzie
,

oraz transmitancji układu zamkniętego

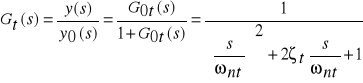
przy czym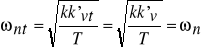
,

.

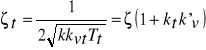
Przy parametrach zastępczych k_vt, T_t, ζ_t pojawia się charakterystyczny współczynnik (1 + k_tk_v'), w przybliżeniu równy wypadkowemu wzmocnieniu w pętli sprzężenia tachometrycznego. Jeśli współczynnik ten jest znacznie większy od jedności, to
, a więc całkowite wzmocnienie prędkościowe układu ze sprzężeniem tachometrycznym, k_vt = k k_vt'≈
zależy tylko od k (w sposób oczywisty) i k_t, a praktycznie nie zależy do k_v'. Zatem rola współczynników wzmocnienia k i k_v' jest nieco inna w układach bez i ze sprzężeniem tachometrycznym. Ze względu na charakter zależności parametrów ω_n i ζ od k, k_v', k_t, T (poleca się wnikliwe rozpatrzenie tych zależności!) możliwe jest wydatne zwiększenie tłumienia bez zmiany częstotliwości drgań własnych lub poszerzenie pasma częstotliwości przenoszonych przez serwomechanizm (miarą tego pasma może być ω_n) i zapewnienie odpowiedniego tłumienia oscylacji w odpowiedzi skokowej.

Należy podkreślić, że podany wyżej opis serwomechanizmu w postaci układu drugiego rzędu jest wprawdzie wystarczający do oceny głównych jego właściwości, ale nie może być stosowany bezkrytycznie:

• przede wszystkim zakładaliśmy proporcjonalność sygnałów, a tym samym założyliśmy liniowość układu; w praktyce mogą występować różnego rodzaju nieliniowości,

• bardziej wnikliwa analiza właściwości serwomechanizmu prowadzi do opisu w postaci układu rzędu wyższego niż drugi; dokonane uproszczenie daje o sobie znać głównie przy ocenie stabilności.

2.3. Zagadnienie jakości w serwomechanizmach

Podstawowym wymaganiem stawianym serwomechanizmom jest stabilność. Precyzyjne definicje i omówienie rodzajów stabilności podane są w ćwiczeniu. Intuicyjnie przez stabilność układu rozumiemy właściwość polegającą na powrocie do stanu równowagi po ustaniu działania wymuszenia, które wytrąciło układ z tego stanu. W tym miejscu będą nas interesować kryteria stabilności - metody praktyczne pozwalające określić na podstawie współczynników równania różniczkowego, transmitancji układu lub jego charakterystyk częstotliwościowych, czy układ jest stabilny i jakie są dopuszczalne zmiany parametrów układu stabilnego - np. wzmocnienia.

W przypadkach układów technicznych, dla których łatwo jest uzyskać charakterystyki częstotliwościowe, korzysta się bardzo często z tak zwanych kryteriów częstotliwościowych oceny stabilności. Najczęściej stosowane kryterium Nyquista dotyczy badania stabilności układu zamkniętego na podstawie charakterystyki G₀(jω) układu otwartego. W praktyce spotyka się najczęściej układy otwarte stabilne. Jeżeli układ otwarty minimalnofazowy jest stabilny, to warunkiem koniecznym i dostatecznym stabilności układu zamkniętego jest, aby dla częstotliwości spełniającej wzór G₀(jω) = 1 przesunięcie fazowe układu otwartego było większe od -π, albo inaczej - dla przesunięcia fazowego -π wzmocnienie układu otwartego G₀(jω) powinno być mniejsze od jedności. Charakterystyki częstotliwościowe mogą być wyznaczone eksperymentalnie lub obliczone na podstawie transmitancji. Na rys. 7a pokazane są charakterystyki częstotliwościowe układu otwartego, który po zamknięciu ujemnego sprzężenia zwrotnego będzie stabilny, a na rys. 7b układu, który po zamknięciu sprzężenia będzie niestabilny.

Wprowadźmy pojęcie zapasu stabilności układu. Zapasem modułu (lub

Rys. 7. Charakterystyki częstotliwościowe układu otwartego:
a) stabilnego po zamknięciu ujemnego sprzężenia zwrotnego;
b) niestabilnego po zamknięciu ujemnego sprzężenia zwrotnego.

amplitudy) nazywamy liczbę d taką, że dG₀(jω_a)=1, gdzie ω_a - zwana częstotliwością graniczną fazy - jest częstotliwością, dla której wykres G_o(jω) przecina ujemną półoś rzeczywistą. Zapasem fazy nazywamy kąt π+arg G₀(jω_m), gdzie ω_m - zwane częstotliwością graniczną modułu - jest częstotliwością, dla której G₀(jω)=1.

Zazwyczaj wymaga się zapasu modułu 8 do 12 dB (w mierze logarytmicznej) oraz zapasu fazy od
do
.

Na podstawie transmitancji operatorowej G(s) można podać transmitancję widmową G(jω). Wykreślając charakterystykę G₀(jω) rozpatrywanego wyżej serwomechanizmu dla różnych wartości parametrów T i k_v oraz stosując przytoczone kryterium stabilności, stwierdzamy, że serwomechanizm jest stabilny dla dowolnych wartości tych parametrów. Układy stabilne dla wszystkich dodatnich wartości swoich parametrów nazywa się strukturalnie stabilnymi. W praktyce serwomechanizmy przy wzroście np. wzmocnienia tracą stabilność. Wynika stąd, że serwomechanizm jest układem wyższego rzędu. Można się o tym przekonać, wyznaczając eksperymentalnie z dużą dokładnością charakterystykę G₀(jω) w szerokim paśmie częstotliwości. Tak więc wyznaczona na podstawie odpowiedzi skokowej stała czasowa serwomechanizmu T jest największą stałą czasową. O stabilności decydują natomiast mniejsze stałe czasowe, które trudno jest wyznaczyć z odpowiedzi skokowej. Jedną z metod zmierzających do zwiększenia zapasu amplitudy i fazy lub zapewnienia stabilności (gdy jej brak) jest stosowanie omówionego wyżej sprzężenia tachometrycznego.

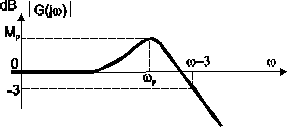
Zdefiniowane wyżej częstotliwości ω_{m i} ω_a dotyczyły układu otwartego. Można też formułować wymagania dla charakterystyk częstotliwościowych układu zamkniętego. Określa się więc częstotliwość rezonansową ω_p, dla której moduł transmitancji układu zamkniętego jest maksymalny (jest to tzw. moduł rezonansowy M_p)

G(jω_p) =
G(jω) = M_p

lub częstotliwość graniczną trzydecybelową ω_-3dB, przy której moduł transmitancji zmniejsza się do wartości 0,707 (-3 dB) - rys. 8. Dla danego układu regulacji wymienione częstotliwości są w przybliżeniu równe i określają tak zwane pasmo robocze, w którym odbywa się odtwarzanie sygnału sinusoidalnego o różnych częstotliwościach z zadaną dokładnością. Pasmo serwomechanizmu może się zawierać w przedziale od zera do ułamków Hz (dla serwomechanizmów dużej mocy lub od zera do kilkudziesięciu Hz (na przykład dla ułamków rejestrujących).

Szereg wymagań dotyczy charakteru przebiegu odpowiedzi y(t) lub uchybu ε(t) serwomechanizm po skokowej zmianie sygnału zadanego. Przebieg uchybu regulacji ε(t) przedstawiono na rys. 9. Jeśli układ jest stabilny, to w przebiegu tym da się wyodrębnić uchyb w stanie ustalonym
, zwany uchybem statycznym. Całkowity uchyb regulacji można przedstawić jako sumę dwóch składowych ε(t) = ε_p(t) + ε_s, gdzie składowa ε_p(t) nazywa się uchybem przejściowym. Uchyb przejściowy dąży do zera z upływem czasu.

Od serwomechanizmu żąda się zerowego uchybu statycznego. Uchyb w stanie ustalonym można obliczyć na podstawie transmitancji układu, korzystając z zależności

Transformata uchybu w rozpatrywanym układzie przy wymuszeniu skokowym A1(t) wyraża się wzorem

.

Wyrażenie G_ε(s) jest nazywane transmitancją uchybową układu regulacji. Uchyb statyczny ε_s jest tylko wtedy równy zeru (niezależnie od amplitudy skoku A), gdy

czyli gdy
.

W układzie serwomechanizmu, ze względu na obecność członu całkującego, zależności te są spełnione, a więc uchyb statyczny jest równy zeru niezależnie od wartości sygnału zadanego. Taki układ regulacji nazywamy astatycznym.

Przy projektowaniu serwomechanizmu można uwzględniać wymagania dotyczące czasu regulacji t_r. Jest on zazwyczaj określony jako przedział czasu od początku wymuszenia do chwili, w której uchyb przejściowy
ε_p(t) = ε(t) - ε_s odpowiedzi skokowej zmniejszy się trwale poniżej 5% swej wartości początkowej (por. rys. 8). Z jednostek osi czasu na rys. 6b wynika, że w rozpatrywanym serwomechaniźmie czas regulacji zależy od częstotliwości drgań własnych
, oraz od współczynnika tłumienia ζ. Stanowi to ogólną własność układów regulacji, gdyż w każdym z nich czas t_r jest w przybliżeniu odwrotnie proporcjonalny do pasma częstotliwości przenoszonego przez układ.

Innym wskaźnikiem jakości regulacji jest tzw. współczynnik przeregulowania χ, określony jako stosunek maksymalnej wartości uchybu przejściowego o znaku przeciwnym niż jego wartość początkowa do wartości początkowej - por. rys. 9.

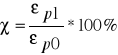
Z rysunku 6b widać, że przeregulowanie χ w badanym serwomechaniźmie zależy jedynie od współczynnika tłumienia ζ. Zazwyczaj przyjmuje się za najkorzystniejsze przeregulowanie od 0% do 40%, co w danym układzie odpowiada tłumieniu ζ= 0,7 - 0,3.

Od serwomechanizmu wymaga się odpowiednio dużej sztywności. Aby wyjaśnić pojęcie sztywności, należy sobie uświadomić, że element wykonawczy serwomechanizmu wywołujący zmianę sygnału wyjściowego y (silnik dokonujący przestawienia obiektu) dysponuje pewnym momentem lub siłą zależną od parametrów konstrukcyjnych układu oraz od wysterowania. W przypadku ε =0 moment ten jest równy zeru, zaś w miarę wzrostu uchybu moment powinien się zwiększać analogia do sprężyny rozciąganej lub ściskanej od położenia początkowego). Można wyznaczyć charakterystykę statyczną M_n'(ε) momentu napędowego serwomechanizmu jako funkcję uchybu ε (rys. 10).

Załóżmy, że w serwomechaniźmie, w którym y₀= const i przebiegi przejściowe ustaliły się, wał wyjściowy obciążamy momentem M_obc (rys. 10). Nowe punkty równowagi wynikają z przecięcia charakterystyk M'_n(ε) i M_obc. A więc dla serwomechanizmu, którego charakterystyka M'_n(ε) jest zaznaczona na rysunku linią 1, nowy punkt równowagi będzie dla ε_s1, a dla serwomechanizmu o charakterystyce M'_n(ε) jak linia 2 - dla ε_s2. Mówimy, że drugi serwomechanizm jest bardziej podatny na obciążenia niż pierwszy lub że pierwszy jest bardziej sztywny niż drugi. Nachylenie charakterystyki M'_n(ε) w punkcie ε=0 nazywa się współczynnikiem sztywności k_s. Sztywność jest parametrem odwrotnym do podatności: im sztywność jest większa, tym podatność na zakłócenia mniejsza.

Współczynnik sztywności wyznacza się zwykle eksperymentalnie. Warto jednak prześledzić wpływ parametrów układu na jego wartość (por. rys. 3a). Przy wyprowadzaniu odpowiedniej zależności będziemy zakładać stan ustalony sygnałów. Napięcie v_m oraz prąd i_m wirnika silnika mają wartości

v_m = k_pkk₀ε,

(
= 0, bo silnik nie obraca się).

Zatem moment napędowy przeniesiony przez przekładnicę I jest określony zależnością

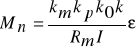
Stąd współczynnik sztywności wynosi

k_s=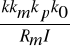
.

Czytelnikom poleca się wnikliwe zinterpretowanie tego wyniku.

Niekiedy wymagania stawiane serwomechanizmom są sprzeczne. Na przykład żądanie dużej sztywności można zrealizować zwiększając wzmocnienie k_v. To z kolei pogarsza zapas stabilności albo nawet prowadzi do niestabilności układu zamkniętego. W praktyce po zapewnieniu wymaganej dokładności statycznej (odpowiednio uchybu statycznego) należy przeprowadzić korekcję właściwości dynamicznych - najczęściej przy użyciu sprzężenia tachometrycznego.

3. NIELINIOWOŚCI WYSTĘPUJĄCE W SERWOMECHANIZMACH

Przedstawiony w punkcie 2 opis właściwości serwomechanizmu opierał się na teorii układów liniowych i dotyczył jego uproszczonego modelu. W rzeczywistości w układach tego typu występują także zjawiska nieliniowe. Omówimy teraz niektóre typy nieliniowości i ich wpływ na właściwości serwomechanizmu.

W układach mechanicznych występuje zjawisko tarcia. Zatem i w silniku, przekładni, obiekcie pobudzanym przez serwomechanizm mamy do czynienia z tym zjawiskiem. Przykładowa charakterystyka momentu tarcia w funkcji prędkości jest przedstawiona na rys. 11. Tarcie w elementach mechanicznych, skończone progi zadziałania wszystkich członów układu wywołują strefę nieczułości na charakterystyce statycznej układu otwartego, tzn., że dla małych wartości sygnałów wejściowych przyrost sygnału wyjściowego jest mniejszy niż dla wartości średnich. Przyczyny wywołujące strefę nieczułości mogą być umiejscowione w różnych częściach układu, jednak wyznaczając ją liczbowo odnosimy ją zazwyczaj do wejścia układu otwartego.

Wzrost wartości sygnału uchybu wywołuje proporcjonalny wzrost sygnałów pośredniczących na wyjściach poszczególnych bloków tylko do pewnej wartości uchybu. Dalsze zwiększanie uchybu wywołuje coraz mniejsze, a nawet może nie wywoływać wcale zmian sygnałów pośredniczących. Jest to efekt nasycenia charakterystyki. Właściwie każdy element przy dostatecznie dużych wartościach sygnałów wejściowych wykazuje nasycenie charakterystyki. O nasyceniu charakterystyki w serwomechaniźmie decyduje element objawiający najwcześniej tę właściwość. W praktyce jest nim z reguły wzmacniacz mocy sterujący element wykonawczy.

Na rys. 12 jest pokazany schemat serwomechanizmu z wymienionymi nieliniowościami. Dla prostoty opisu i analizy zwykle przyjmuje się aproksymacje charakterystyk członów nieliniowych odcinkami prostych. Nieliniowości te wpływają zarówno na dokładność serwomechanizmu, pogarszając ją, jak i na właściwości dynamiczne.

Rys. 12. Schemat serwomechanizmu z nieliniowościami charakterystyk statycznych

Badając charakterystykę częstotliwościową serwomechanizmu słabo tłumionego można stwierdzić jej nieciągłość dla pewnych częstotliwości zależnych do amplitudy sygnału wejściowego i niejednoznaczność przy zwiększaniu i zmniejszaniu częstotliwości. Zjawiska te - zwane rezonansem skokowym - występują w strefie częstotliwości drgań własnych i są spowodowane występowaniem w układzie elementów nieliniowych o jednoznacznych charakterystykach - z nasyceniem lub silną zależnością współczynnika od sygnału wejściowego. Obserwuje się przy tym efekt jak gdyby odchylenia samego wierzchołka charakterystyki amplitudowej w lewo lub w prawo w zależności od typu nieliniowości. Na przykład dla częstotliwości bliskich ω_p, gdy amplituda odpowiedniego sygnału jest wystarczająca do wejścia w zakres nasycenia, średni współczynnik wzmocnienia maleje i zastępcza częstotliwość drgań własnych przesuwa się w lewo (rys. 13).

Występujące w serwomechaniźmie ujemne sprzężenie zwrotne zmniejsza wpływ nieliniowości na jego pracę. Korzystny jest zwłaszcza wpływ sprzężenia tachometrycznego, gdyż umożliwia zwiększenie sztywności układu, a więc zmniejszenie wpływu tarcia (strefy nieczułości pochodzącej od tego tarcia).

PYTANIA KONTROLNE:

1. Podać zasadę działania, zastosowanie i schemat badanego serwomechanizmu.

2. Podać odpowiedź na typowe wymuszenie skokowe serwomechanizmu z otwartą i zamkniętą pętlą sprzężenia zwrotnego.

3. Kryteria jakości działania serwomechanizmów.

4. Przyczyny uchybów w badanym serwomechaniźmie.

5. Wpływ wzmocnień k, k₀ na charakterystyki skokowe serwomechanizmu.

6. Napisać równanie serwomechanizmu z uwzględnieniem indukcyjności wirnika.

7. Jakimi przesłankami należy się kierować przy wyborze silnika serwomechanizmu jeśli pomijamy wpływ tarcia?

8. Wyjaśnić paradoks: astatyzm serwomechanizmu a występowanie uchybu ustalonego w serwomechaniźmie rzeczywistym.

9. Co to jest sprzężenie tachometryczne i jaki jest jego wpływ na pracę układu.

10. Wyjaśnić jak będzie zachowywał się serwomechanizm dla małych i bardzo dużych wartości wzmocnień.

OPIS STANOWISKA LABORATORYJNEGO

Na rys. 14 podany jest schemat blokowy znajdujący się na płycie czołowej badanego serwomechanizmu. Sygnał zadany y₀ uzyskuje się z potencjometru 10-obrotowego ustawianego ręcznie, zaś sygnał y na potencjometrze P₀ sprzężonym z silnikiem wykonawczym /można odczytać tylko część pełnego obrotu/.

Sygnał ε= y₀ - y + w (w - dodatkowy sygnał zewnętrzny) jest wstępnie wzmacniany we wzmacniaczu o regulowanym wzmocnieniu k, następnie sumowany z sygnałem ujemnego sprzężenia tachometrycznego. Sygnał sprzężenia tachometrycznego uzyskuje się z silnika prądu stałego pracującego jako prądnica tachometryczna, w której

gdzie α - kąt obrotu silnika wykonawczego, k_p - współczynnik wzmocnienia prądnicy tachometrycznej.

Wzmocnienie w pętli sprzężenia tachometrycznego jest regulowane potencjometrem k_t.

Wypadkowy sygnał
jest ponownie wzmacniany we wzmacniaczu o regulowanym współczynniku wzmocnienia k₀.

Sygnał wyjściowy wzmacniacza steruje silnikiem wykonawczym sprzężonym z potencjometrem wyjściowym, przetwarzającym położenie kątowe silnika na sygnał napięciowy. Jako element wykonawczy zastosowano silnik obrotowy prądu stałego.

Do przeprowadzenia badań serwomechanizmu należy wykorzystać następujące przyrządy:

• stojak laboratoryjny SERWOMECHANIZM

• oscyloskop wolnych przebiegów STD 501 XY

• rejestrator 5-kanałowy H-327-5

• woltomierz cyfrowy prądu stałego V-540

• przewody ekranowane

PROGRAM ĆWICZENIA.

1. Zbadać działanie serwomechanizmu bez pętli sprzężenia zwrotnego; w tym punkcie należy przygotować stanowisko do pomiaru poprzez wyłączenie sygnału wymuszającego Y₀ i ustawienie wartości wzmocnień w torze głównym na 75% skali oraz załączenie do czasu ustalenia obrotów sygnału sprzężenia zwrotnego. Gdy tarcza przestanie się obracać wyłączyć sprzężenie zwrotne a następnie uruchomić rejestrację na komputerze i w chwile później załączyć sygnał zadawany Y₀.

2. Zbadać działanie serwomechanizmu w układzie zamkniętym przy maksymalnych wartościach wzmocnień K, K₀. Praktyczna realizacja tego punktu oraz pkt. 3, 4 polega na wyłączeniu sygnału Y₀ i załączenia sprzężenia w torze głównym Y. Po ustaleniu obrotów tarczy odbiorczej (Uwaga! w tym punkcie ze względu na duże wartości wzmocnień tarcza będzie oscylowała wokoło wartości początkowej) należy uruchomić rejestrację na komputerze a następnie podać sygnał Y₀.

3. Zbadać i zarejestrować działanie serwomechanizmu w układzie zamkniętym przy prawie minimalnych wartościach wzmocnień. W tym punkcie należy wydłużyć czas rejestracji.

4. Dobrać wartości optymalne wzmocnień w torze głównym tak aby serwomechanizm osiągnął wartość zadaną w jak najkrótszym czasie. Polega to praktycznie na uzyskaniu przeregulowania a następnie stopniowym zmniejszaniu wzmocnienia. W tym punkcie należy zarejestrowac dwa przebiegi: z przeregulowniem i optymalny.

5. Zbadać wpływ sprzężenia tachometrycznego i wartości wzmocnienia K_t Ustawić optymalne wartości wzmocnień uzyskane w pkt. 4 a następnie załączyć sprzężenie tachometryczne i regulować wartość K_t.

6. Dla włączonych wszystkich sprzężeń dobrać metodą podaną w pkt. 4 optymalny przebieg.

ZAKRES SPRAWOZDANIA:

Sprawozdanie powinno zawierać:

1. opis wpływu wzmocnienia w torze głównym,

2. wpływ sprzężenia Y,

3. wpływ sprzężenia tachometrycznego,

4. opis wpływu wzmocnienia K_t,

LITERATURA:

1. Frelek i inni: Laboratorium podstaw automatyki. Politechnika Warszawska 1980 r.

2. K. Amborski i inni: Laboratorium podstaw automatyki. Politechnika Warszawska 1976 r.

Uwaga: Dalej termin częstotliwość będzie używany również przy operowaniu pulsacja ω=2πf.

1

17

Serwomechanizm

Rys. 1. Struktura układu regulacji

Obiekt sterowany

Informacja początkowa o celu sterowania (sygnał zadany

Zakłócenia

Urządzenie sterujące

Sygnał wejściowy

Sygnał wyjściowy

k₀

P

O

S

Pr

k₀

V_y0

y₀

V

I

y

V_y

i_w

V_t

V_ε

V_m

P₀

+

−

α

Rys. 2. Schemat ideowy serwomechanizmu

Rys. 3. Schemat blokowy serwomechanizmu: a) pełny, b) uproszczony

b)

y(s)

y₀(s)

-

+

-

+

k_ts

T_B

k

a)

y

V_y

V_t



V

V

-

+

-

y_o

k_ts

k_p

I

T_A

k_o

k

k_p

P

K₀

K

ε

−

−

+

+

+

Y₀

W

P₀

+−

y₀

y

k_p k k₀

I

V_m

+

V_yo

U

Y

Y

K_t

Prądnica tachometryczna

Silnik

Rys. 14. Schemat stanowiska laboratoryjnego

Rys. 9. Pojęcie uchybu ustalonego, przejściowego oraz czasu regulacji.

Rys. 8. Typowy przebieg charakterystyki
częstotliwościowej serwomechanizmu

Rys. 4. Charakterystyka skokowa układu
otwartego prostego serwomechanizmu

Rys. 5. Charakterystyka impulsowa układu otwartego prostego serwomechanizmu

---