Agnieszka Magiera, Ewelina Zielińska
Sprawozdanie ćw.8 :
Wyznaczanie energii aktywacji reakcji zmydlania estru
1. Wstęp teoretyczny:
Teoria zderzeń aktywnych
Zgodnie z tą teorią cząsteczki mogą z sobą reagować gdy zbliżą się do siebie na dostatecznie małą odległość tzn. gdy się zderzą. W wyniku oddziaływania pomiędzy elektronami dochodzi do zerwania wiązań w cząsteczkach substratów i utworzenia nowych, charakterystycznych dla produktów reakcji. Nie wszystkie zderzenia prowadzą do powstania nowych cząsteczek (produktów), a więc nie wszystkie prowadzą do zajścia reakcji chemicznej. Aby reakcja zaszła, cząsteczki muszą zderzyć się z dostatecznie dużą energią, wówczas dochodzi do przegrupowania atomów w cząsteczkach i przebudowy struktury wiązań. Zderzenia takie nazywane są zderzeniami efektywnymi (aktywnymi), a energia jaką muszą mieć w sumie cząsteczki substratów aby do takiego zderzenia doszło, nie może być mniejsza od pewnej wartości progowej nazywanej energią aktywacji.
Warunek o odpowiedniej wartości energii musi być zawsze zachowany aby reakcja mogła zachodzić, jest to więc warunek konieczny. Nie zawsze jednak jego spełnienie jest wystarczające do zajścia reakcji. O możliwości zajścia reakcji decyduje również wzajemne ułożenie cząsteczek względem siebie, a wiec ich orientacja w przestrzeni. Biorąc jako przykład reakcję syntezy jodowodoru można pokazać (Rysunek 2), że w zależności od tego jak cząsteczki jodu i wodoru ustawią się względem siebie reakcja chemiczna może zajść lub nie.
Gdyby każde zderzenie prowadziło do reakcji, w warunkach normalnych reakcja ta przebiegałaby bardzo szybko, natomiast w rzeczywistości zachodzi z niezauważalną szybkością.
Teoria kompleksu aktywnego
Pomiary wskazują na to, że podczas zderzenia cząsteczek H2 i I2 nie następuje gwałtowne zerwanie tych wiązań, a jedynie ich rozluźnienie. Do rozerwania wiązania H-H i I-I trzeba dostarczyć energię równa energii dysocjacji cząsteczek H2 i I2, które wynoszą odpowiednio EH-H = 436,6kJ/mol i EI-I =151,6kJ/mol. Tymczasem energia potrzebna do tego aby zaszła reakcja H2(g) + I2(g) → 2HI(g) wynosi zaledwie 171,8kJ/mol, a wiec jest znacznie mniejsza od sumy energii dysocjacji cząsteczek H2 i I2. W związku z tym przyjmuje się, że cząsteczki te przekształcając się w cząsteczki H-I muszą przejść przez pewien stan pośredni (pewien układ atomów) zwany kompleksem aktywnym, w którym następuje osłabienie starych wiązań i częściowe utworzenie nowych wiązań. Kompleks aktywny może się przekształcić w produkty, bądź rozpaść na wyjściowe substraty reakcji
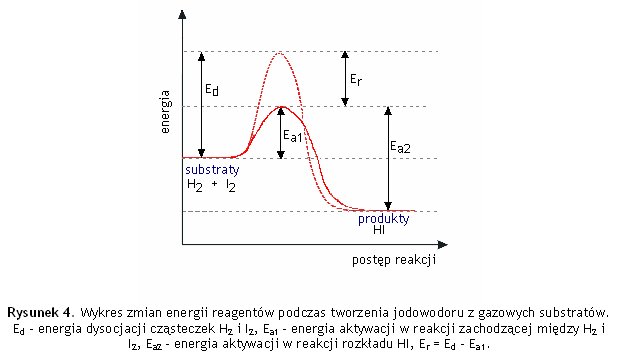
Z powyższych rozważań wynika, że przekształcenie cząsteczek w produkty, przebiegające przez stadium kompleksu aktywnego wymaga znacznie mniejszego nakładu energii niż gdyby przebiegało poprzez zerwanie wszystkich wiązań i wytworzenie swobodnych atomów
Na rysunku przedstawiono porównanie zmian energii wewnętrznej układu w przypadku gdy reakcja biegnie przez stan pośredni-kompleks aktywny, ze zmianami energii w przypadku gdyby reakcja biegła z dysocjacją cząsteczek substratów na atomy. Energia wewnętrzna układu jest energią wynikającą z ruchów i oddziaływań cząsteczek a także energią oddziaływań elektronów i jąder tych cząsteczek.
Na wykresie jest widoczne, że średnia energia cząsteczek substratów nie wystarcza do zajścia miedzy nimi reakcji chemicznej, dopiero dostarczenie energii (najczęściej ogrzewa się mieszaninę reakcyjną) pozwala na uzyskanie energii wystarczającej do utworzenia kompleksu aktywnego. Kompleks aktywny przekształcając się w cząsteczki produktów oddaje nadmiar energii.
Na podstawie teorii kompleksu aktywnego można uściślić pojęcie energii aktywacji. Tak wiec energia aktywacji jest różnicą pomiędzy wartością energii kompleksu aktywnego i energii substratów, inaczej mówiąc jest to najmniejsza wartość energii niezbędnej do utworzenia kompleksu aktywnego.
Poniżej znajduje się porównanie definicji energii aktywacji obu teorii:
definicje energii aktywacji w teorii zderzeń aktywnych i w teorii kompleksu aktywnego |
|
W teorii zderzeń aktywnych energię aktywacji definiuje się jako minimalną energię, jaką muszą posiadać cząstki (drobiny) reagentów, aby ich zderzenie było efektywne, niezbędne do zapoczątkowania reakcji. Jakie zderzenia są efektywne? Cząsteczki muszą być względem siebie odpowiednio zorientowane w momencie zderzenia (czynnik steryczny) oraz muszą posiadać minimalną progową wartość energii (czyli energię aktywacji). |
W teorii kompleksu aktywnego energia aktywacji jest minimalną energią niezbędną do utworzenia kompleksu aktywnego. |
REAKCJE ESTRÓW
Estry wykazują właściwości chemiczne podobne do właściwości innych pochodnych kwasów karboksylowych, jednakże są one znacznie mniej reaktywne w reakcjach z nukleofilami niż chlorki i bezwodniki kwasowe. Na rysunku przedstawiono niektóre ogólne reakcje estrów, wszystkie one dotyczą zarówno estrów acyklicznych, jak i estrów cyklicznych (laktonów).
Hydroliza - przekształcenie estrów w kwasy karboksylowe. Estry można hydrolizować zarówno w wodnym roztworze zasady, jak i w wodnym roztworze kwasu. Produktem reakcji jest kwas karboksylowy oraz alkohol.
Reakcja estrów w środowisku zasadowym nazywana jest reakcją zmydlania. Reakcja zmydlania przebiega według typowego schematu reakcji substytucji nukleofilowej grupy acylowej. W reakcji tej jon hydroksylowy OH- jest nukleofilem, który przyłącza się do atomu węgla grupy karbonylowej w estrze, tworząc w ten sposób tetraedryczny produkt pośredni. W następnym etapie następuje odszczepienie jonu alkoksylowego, co prowadzi do powstania cząsteczki kwasu karboksylowego, który ulega deprotonowaniu (odszczepia proton) tworząc jon karboksylanowy. Kwas karboksylowy uzyskuje się w następnym etapie przez dodanie do środowiska reakcji wodnego roztworu HCl w celu protonowania jonu karboksylanowego (następuje przesunięcie równowagi dysocjacji kwasu w stronę struktury niezdysocjowanej). Hydroliza estrów w warunkach kwasowych może przebiegać według więcej niż jednego mechanizmu, co w wielu przypadkach zależy od struktury substratu. Najczęściej jednak reakcja ta przebiega wg mechanizmu reakcji estryfikacji Fischera. W pierwszym etapie następuje aktywowanie cząsteczki estru poprzez protonowanie grupy karbonylowej, a następnie na tak aktywowany atom węgla następuje atak nukleofolowy cząsteczki wody. Przeniesienie protonu i eliminacja cząsteczki alkoholu daje jako produkt końcowy - kwas karboksylowy.
Estry ulegają kwasowej i zasadowej hydrolizie. Reakcja hydrolizy jest reakcjąodwrotną do reakcji estryfikacji. Zdolność do ulegania reakcji hydrolizy maleje zewzrostem długości łańcucha estru.
Hydroliza zasadowa
Przykładem reakcji hydrolizy zasadowej jest reakcja octanu metylu z wodorotlenkiem potasu. W wyniku tej reakcji powstaje sól- octan potasu i alkoholmetanol.
Produkty nie reagują ze sobą, dlatego też jest to reakcja nieodwracalna. Hydroliza potocznie była nazywana zmydlaniem lub saponifikacja gdyż wykorzystywano tą reakcję do otrzymywania mydeł.
Estry maja zdolność do łatwej hydrolizy, która przebiega w zależności od pH na dwa sposoby:
sposób odwracalny zachodzący w niskim pH (środowisko kwaśne) ester w wodzie hydrolizuje na alkohol i kwas,
sposób nieodwracalny zachodzący przy wysokim pH (środowisko zasadowe) ester hydrolizuje na alkohol i odpowiednią sól kwasu; jest to tzw. saponifikacja (zmydlanie) estrów
2. Obliczenia
Obliczyłyśmy H0 i Czo dla temperatury 23 i 35 stopni Celsjusza:
H0 dla t=23oC wyniosła: Ho=98,2[m-1]∙0,00924[Ω-1]=0,907368 [m-1 Ω-1]
Otrzymujemy Czo=0,907368/[190*(1+0,019*(23-18))]= 0,004361298
H0 dla t=35oC wyniosła: H0=98,2 [m-1]∙0,01663[Ω-1]=1,633066[m-1 Ω-1]
Otrzymujemy Czo= 0,83968 /[190*(1+0,019*(35-18))]= 0,006496662
Po przegotowaniu, kiedy reakcja całkowicie zaszła, przewodnictwo H0 dla 0,1M NaOH+0,1M ester w temperaturze t=23oC wyniosła: H0=98,2[m-1]∙0,00426[Ω-1]= 0,418332[m-1 Ω-1]
A w temperaturze t=35oC wyniosła: H0=98,2[m-1]∙0,0043 [Ω-1]= 0,42226 [m-1 Ω-1]
Obliczamy :
Na podstawie wartości uzyskanych z doświadczenia obliczyłyśmy wymienione w tabelach wartości korzystając z poniższych wzorów:
![]()
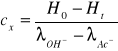
gdzie wartość różnicy ![]()
jest stała w toku reakcji i wynosi ![]()
.
![]()
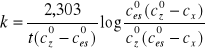
Dla t=23oC K=98,2 [m-1], Czo=4,36![]()
[mol∙dm-3] oraz Ceso=3,55![]()
[mol∙dm-3]
T [oC] |
t [min] |
S
|
H0 [Ω-1∙m-1] |
Cx [mol∙dm-3] |
k [dm3∙mol-1∙min-1] |
23 |
0 |
9,51 |
0,780 |
0,28 |
450,694 |
23 |
2 |
7,58 |
0,622 |
1,33 |
78,501 |
23 |
4 |
6,67 |
0,547 |
1,83 |
68,712 |
23 |
6 |
6,11 |
0,501 |
2,14 |
64,402 |
23 |
8 |
5,57 |
0,457 |
2,43 |
68,560 |
23 |
10 |
5,50 |
0,451 |
2,47 |
57,562 |
23 |
12 |
5,33 |
0,437 |
2,56 |
54,154 |
23 |
14 |
5,18 |
0,425 |
2,64 |
51,952 |
23 |
16 |
5,05 |
0,414 |
2,71 |
50,385 |
23 |
18 |
4,96 |
0,407 |
2,76 |
48,261 |
23 |
20 |
4,88 |
0,400 |
2,81 |
46,548 |
Średnia wartość k dla 23oC = 58,904
Dla t=35oC K=98,2[m-1], Czo= 0,0040, Ceso= 0,0039
T [oC] |
t [min] |
S [Ω-1] |
Ho [Ω-1∙m-1] |
Cx [mol∙dm-3] |
k [dm3∙mol-1∙min-1] |
35 |
0 |
6,2 |
0,508 |
1,87 |
10113,005 |
35 |
2 |
4,28 |
0,351 |
2,76 |
1765,825 |
35 |
4 |
3,92 |
0,321 |
2,93 |
758,568 |
35 |
6 |
3,88 |
0,318 |
2,95 |
418,223 |
35 |
8 |
3,9 |
0,320 |
2,94 |
345,135 |
35 |
10 |
3,9 |
0,320 |
2,94 |
276,108 |
35 |
12 |
3,9 |
0,320 |
2,94 |
230,090 |
35 |
14 |
3,9 |
0,320 |
2,94 |
197,220 |
35 |
16 |
3,89 |
0,319 |
2,95 |
164,551 |
35 |
18 |
3,88 |
0,318 |
2,95 |
139,408 |
35 |
20 |
3,86 |
0,317 |
2,96 |
113,745 |
Średnia wartość k dla 35oC = 364,84
Na kolejnej stronie zamieszczamy wykres zależności 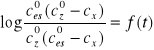
dla obu temperatur.
Obliczone współczynniki kierunkowe oraz k obliczone ze wzoru ![]()
wynoszą:
Dla temperatury 23 a=0,0108, k= 95,182
Dla temperatury 35: a= 0,0127, k=135,180
Korzystając z równania Arrheniusa, obliczam współczynnik temperaturowy reakcji i jej energię aktywacji.
Współczynnik temperaturowy=
=
= 1,42
1Obliczenia energii aktywacji:
Równanie Arrheniusa: ![]()
czyli ![]()
,
Gdzie A=
, więc Eak=A∙2,303∙R
Stałą A dla tej reakcji odczytujemy z wykresu: ![]()
z wartości:
k |
logk |
1/T |
95,182 |
1,979 |
3,38 |
135,180 |
2,131 |
3,25 |
![]()
Współczynnik a=--25,388 b=1,912
a= -A ![]()
a= -(-25,388 )= 25,388
Eak =A∙2,303∙R=25,388 ∙2,303∙8,314[J/mol]
Eak =48,611 [kJ/mol] = jest średnią wartością energią aktywacji d11a przedziału temperatur od 23oC
Do sprawozdania dołączamy również wykresy zależności H=f(t) na którym wyraźnie widać zależność przewodnictwa od czasu przebiegania reakcji. Wraz ze wzrostem czasu reakcji przewodnictwo roztworu maleje. Spowodowane jest to zmianą (zmaleniem) stężenia zasady której przewodnictwo jest wysokie.
.
3. Wnioski
Wartość średniej stałej szybkości reakcji w poszczególnych temperaturach wyliczone z równań oraz wartość otrzymana metodą graficzną nie różnią się znacząco.
Współczynnik temperaturowy równy 1,42 jest liczbą wskazującą, ile razy wzrasta szybkość reakcji po podwyższeniu temperatury o 12 stopni. Współczynnik temperaturowy nie jest jednak stały. Zmienia się zależnie od rodzaju reakcji i od temperatury. Im wyższa temperatura, współczynnik jest mniejszy i dąży do jedności. Współczynnik temperaturowy daje jedynie przybliżony obraz wpływu temperatury na szybkość reakcji. W porównaniu z wartością tablicową otrzymana w doświadczeniu jest przybliżona. Wartość tablicowa wynosi 1,4.
Jeżeli energia aktywacji Ea jest mała, to szybkość reakcji zmienia się nieznacznie wraz ze zmianą temperatury. Przeciwnie jest, gdy Ea jest duża - wówczas nachylenie krzywej jest strome, a szybkość reakcji bardzo silnie zależy od temperatury. W tym przypadku Energia aktywacji wynosi 48,611 kJ/ mol więc szybkość reakcji silnie zależy od temperatury. W porównaniu z wartością tablicową otrzymana w doświadczeniu jest przybliżona. Wartość tablicowa wynosi46,9kj/mol.
W doświadczeniu dla temperatury otrzymaliśmy punkt odbiegający dla wartośći k, wynikać to może z niedokładności pomiaru spowodowanej za krótkim czasem czekania na ustabilizowanie wartości pomiaru lub bąbelkami znajdującymi się w roztworze.
Podczas wykonywania przez nas doświadczenia, pojawiły się problemy ze sprzętem.
![]()
Wyszukiwarka
Podobne podstrony:
Pojęcia na egzamin z metali, Chemia Fizyczna, chemia fizyczna- laborki rozne, Rozne
mmgg, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II sprawka
Ćwiczenie 1 - oznaczanie stalej i stopnia dysocjacji, Biotechnologia PWR, Semestr 3, Chemia fizyczna
Korelacja liniowa, fizyczna, chemia fizyczna, Fizyczna, CH. FIZYCZNA, laborki sprawozdania fizyczna
Fizyczna ćw 4, fizyczna, chemia fizyczna, Fizyczna, CH. FIZYCZNA, laborki sprawozdania fizyczna
ogniwa galwaniczne, fizyczna, chemia fizyczna, Fizyczna, laborki
spr57, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy
Moje 50 , Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II spr
monia 11, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II spr
15 wyznaczanie ciepła spalania, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, Chem
Chemia a ochrona środowiska - referat, Chemia Fizyczna, chemia fizyczna- laborki rozne, Rozne
Dane, fizyczna, chemia fizyczna, Fizyczna, CH. FIZYCZNA, laborki sprawozdania fizyczna
teoria 1, fizyczna, chemia fizyczna, Fizyczna, laborki
KOND41vmac, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II s
Katalizatory - referat, Chemia Fizyczna, chemia fizyczna- laborki rozne, Rozne
rad, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II sprawka
kalorymetria2, fizyczna, chemia fizyczna, Fizyczna, laborki
więcej podobnych podstron