Nr ćwiczenia	Temat ćwiczenia				Ocena z teorii
8	Drgania tłumione w obwodzie RLC
Nr zespołu	Nazwisko i imię				Ocena zal. ćwiczenia:
6	Lesiak Michał
Data	Wydział	Rok	Grupa		Uwagi:
16 III 2006	EAI i E	I	3

Cel ćwiczenia

Obserwacja przebiegów napięcia w obwodzie RLC. Pomiar parametrów opisujących rozwiązanie równania różniczkowego modelującego obwód RLC.

Opracowanie teoretyczne

Prawa Kirchhoffa

I prawo Kirchhoffa: wektorowa suma wszystkich natężeń prądu dopływających do punktu rozgałęzienia w obwodzie elektrycznym równa jest zeru (inaczej: suma natężeń prądów wpływających do punktu rozgałęzienia równa jest sumie natężeń prądów wypływających).

II prawo Kirchhoffa: suma spadków napięcia w każdym zamkniętym obwodzie elektrycznym równa jest zewnętrznej sile elektromotorycznej SEM działającej na ten obwód.

Napięcie na oporniku, cewce i kondensatorze

Na oporniku napięcie rośnie wraz ze wzrostem prądu płynącego w obwodzie i nie zależy od częstotliwości.

Na kondensatorze odkłada się tym większe napięcie im niższa jest częstotliwość, gdyż rośnie wtedy jego reaktancja.

Na cewce odkłada się tym większe napięcie im wyższa jest częstotliwość, gdyż reaktancja cewki rośnie wraz z częstotliwością.

Obwód RLC

Obwód RLC składa się z cewki, kondensatora i oporu. Tak zbudowany obwód jest źródłem drgań tłumionych.

Uc +UR +UL = 0, gdzie kolejno oznaczyłem napięcia: kondensatora, opornika i cewki.

- II prawo Kirchoffa

podstawiając:
i

gdzie β - współczynnik tłumienia

ω₀­ - częstość kołowa drgań harmonicznych swobodnych

otrzymujemy:

Dla tłumienia słabego tzn. ၢ < ၷ, rozwiązanie równania tłumienia drgań jest następujące:

- częstość drgań tłumionych (mniejsza od częstości drgań nietłumionych),

Dla ၢ > ၷ rozwiązaniem jest funkcja wykładnicza (tłumienie powoduje zanik drgań).

Gdy ၷ = ၢ mamy do czynienia z tłumieniem krytycznym, który jest tanem przejściowym pomiędzy wyżej wymienionymi przypadkami

Rozwiązanie tego układu istnieje gdy:

Tłumienie słabe:
Tłumienie silne:

Tłumienie krytyczne:
Przejście drgań periodycznych w aperiodyczne zachodzi dla tej ustalonej wartości oporu R nazywanej oporem krytycznym.

Logarytmiczny dekrement tłumienia

rozpatrując kolejne amplitudy

dekrement tłumienia jest miarą „oporu”

Przebieg aperiodyczny

Jest to przebieg, który gaśnie po pierwszym wychyleniu.

Zasada działania oscyloskopu

Głównym elementem oscyloskopu jest lampa oscyloskopowa. Na jej ekranie powstaje obraz świetlny obserwowanych sygnałów lub wielkości. Obraz świetlny widoczny na ekranie oscyloskopu jest wynikiem bombardowania ruchomą wiązką elektronów warstwy luminoforu pokrywającej wewnętrzną powierzchnię ekranu. Źródłem wiązki jest działo elektronowe. Katoda emituje elektrony, które następnie przyspieszane są w polu elektrycznym kolejnych anod działa elektronowego. Parametry wiązki takie jak prędkość elektronów w strumieniu i średnica strumienia decydujące o jakości obserwowanego obrazu można regulować pokrętłami panelu czołowego opisanymi jako JASNOŚĆ (INTENSITY) i OSTROŚĆ (FOCUS).
Wyemitowana przez działo elektronowe wiązka jest następnie odchylana zmiennym polem elektrycznym w dwóch układach odchylania: pionowego-Y (VERTICAL) i poziomego-X (HORIZONTAL). Zmiany pola elektrycznego w układach odchylania, wymuszone zmianami napięcia przyłożonego do płytek odchylających, powodują że wiązka elektronów uderza w co raz to inne punkty ekranu powodując ruch plamki świetlnej obserwowany jako obraz oscyloskopowy.

Opracowanie wyników

1. Obliczam współczynnik dekrementu tłumienia drgań badanego obwodu:

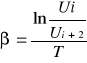
L [H]	R [Ω]	T [s]	U2 [V]	U4 [V]	U6 [V]	β1 [1/s]	β2 [1/s]	βŚR [1/s]
0,003	0	0,00028	7,6	5,8	4,4	965	987	976
0,003	5	0,00029	5	3,2	2	1539	1621	1580
0,001	0	0,000165	7,4	5,6	4,4	1689	1462	1575
0,001	3	0,000165	5	3	1,8	3096	3096	2919

2. Obliczam rezystancję pasożytniczą cewki:

L [H]	β [1/s]	Rp [Ω]
0,003	976	Rp = 2* 976 * 0,003 = 5,9
0,001	1575	Rp = 2* 1575 * 0,001 = 3,15

3. Obliczam pojemność kondensatora:

;
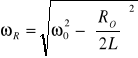
; R_O=R+R_p ;

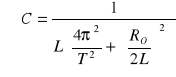
L [H]	R [Ω]	T [s]	Rp [Ω]	C [nF]
0,003	5	0,00029	5,9
0,001	3	0,000165	3,15

4. Obliczam błąd wyznaczenia pojemności C metodą różniczki zupełnej:

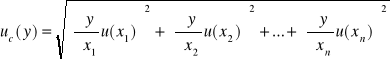
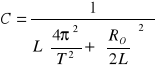
, czyli C(T, R_O), bo L=const, zatem:

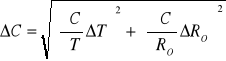
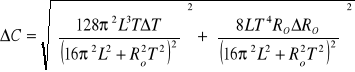
Szukamy ΔR₀:

R₀=R+R_p , R=const
∆R₀₌∆R_p

R_p=2βL=
L=const, czyli R_p(T,U₂,U₄) zatem:

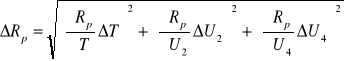
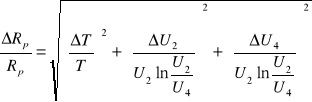
1) Dla L=0,003H, R=5Ω, Rp=5,9Ω, T=0,00028s, ∆T=0,00002s, ∆U₂=0,2V, ∆U₄=0,2V, U₂=5V, U₄=3,2V

∆R₀ =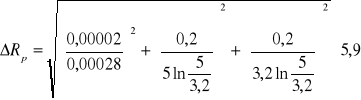
=1,068 Ω

Błąd pomiaru ∆C:

R₀=10,9 Ω

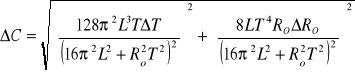
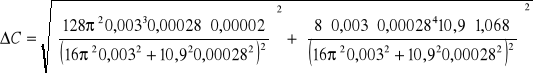
=97 [nF]

2) Dla L=0,001H, R=3Ω, Rp=3,15Ω, T=0,000165s, ∆T=0,00001s, ∆U2=0,2V, ∆U₄=0,2V, U₂=5V, U₄=3V

∆R₀ =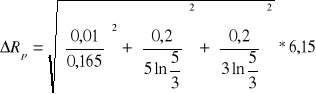
=1,007Ω

R₀=6,15Ω

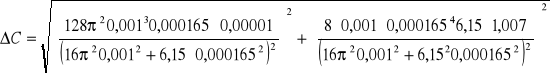
= 83 [nF]

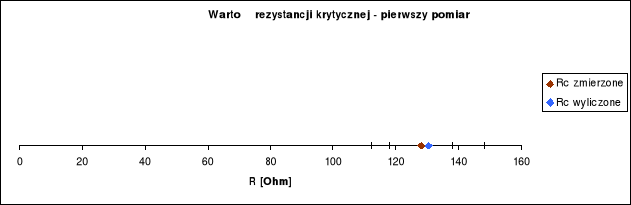
5. W przypadku przebiegu aperiodycznego porównuję zmierzoną wartość rezystancji krytycznej z wartością teoretyczną obliczoną ze wzoru:

1) C=705 nF, L=0,003H

=130Ω

Odchylenie standardowe pomiaru pośredniego, L=0,003H=const, C=705*10^-9 F
ΔC=97*10^-9 F

ΔR_C-WYLICZONE=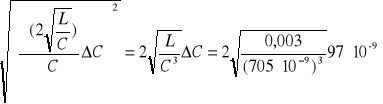
=18Ω

Zmierzone: R_C-ZMIERZONE=128Ω ΔR_C-ZMIERZONE=10Ω

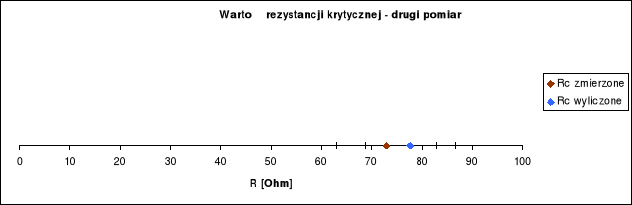
2) C=662 nF, L=0,001H

R_C-WYLICZONE = 76 Ω

L=0,001H=const, C=0,662*10^-6 F ΔC=0,258*10^-6 F

Analogicznie:

ΔR_C-WYLICZONE=9Ω

Zmierzone: R_C-ZMIERZONE=73Ω ΔR_C-ZMIERZONE=10Ω

Wnioski:

Wyniki eksperymentu w znacznym stopniu pokrywają się z oczekiwaniami teoretycznymi mieszcząc się w granicach błędu. Na błędy znaczący wpływ mogły mieć błędne odczyty wykresów oscylatora. Nie bez znaczenia było także założenie bezbłędnego pomiaru cewki oraz kondensatora, co wpływało na określenie błędu.

Najbardziej dyskusyjnym wydaje się być błąd pomiarowy rezystancji krytycznej - trudność polegała na ocenie momentu przejścia z drgań aperiodycznych do periodycznych (co wynikało także z niedostatecznej dokładności oscyloskopu), dlatego przyjąłem dość znaczny błąd rzędu 10Ω, chociaż widać, że różnica nie przekracza wartości 3Ω.

Podsumowując, eksperyment w zadowalającym stopniu potwierdził słuszność teoretycznych rozważań.

---