Sikora Tomasz
Marcin Tartas
Rafał Wolski
Grupa L6/II
Optyka geometryczna
Data oddania 12.06.2007
Data wykonywania ćwiczenia: 22.05.2007
LABORATORIUM OPTOELEKTRONIKI
1. Cel ćwiczenia:
Celem ćwiczenia było zapoznanie się z budową i zasadą działania teleskopów. Keplera i Galileusza, na podstawie których sprawdzaliśmy podstawowe optyki geometrycznej.
2. Wstęp teoretyczny:
Optyka to dział fizyki, zajmujący się badaniem natury światła, prawami opisującymi jego emisję, rozchodzenie się, oddziaływanie z materią oraz pochłanianie przez materię. Optyka wypracowała specyficzne metody pierwotnie przeznaczone do badania światła, stosowane obecnie także do badania rozchodzenia się innych zakresów promieniowania
elektromagnetycznego podczerwień, ultrafiolet zwane światłem niewidzialnym.
Optyka geometryczna, najstarsza i podstawowa do dziś część optyki. Wprowadza pojęcie promień świetlny jako cienką strużkę światła (odpowiednik prostej w geometrii). Opisuje rozchodzenie się światła jako bieg promieni, bez wnikania w naturę światła. Według optyki geometrycznej, światło rozchodzi się w ośrodkach jednorodnych po liniach prostych, na granicy ośrodków ulega odbiciu a przechodząc do drugiego ośrodka ulega załamaniu.
Teleskop - przyrząd optyczny złożony z dwóch elementów optycznych: obiektywu i okularu (teleskop soczewkowy) lub z okularu i zwierciadła (teleskop zwierciadlany) połączonych tubusem. Służy do powiększania odległych obrazów. Zarówno teleskop soczewkowy, jak i teleskop zwierciadlany dają obraz rzeczywisty powiększony, odwrócony. Buduje się wiele rodzajów teleskopów od prostych przyrządów optycznych służących do obserwacji krajobrazu po złożone urządzenia stosowane w astronomii.
Najbardziej podstawowymi typami teleskopów soczewkowych są teleskopy Keplera i Galileusza. Wspólną cecha teleskopów jest to, że odległość między ich soczewkami jest równa sumie ogniskowych obu soczewek (uwzględniając, że ogniskowa soczewki skupiającej jest dodatnia, a soczewki rozpraszającej - ujemna).
Teleskop Keplera składa się z dwóch soczewek skupiających S1 i S2 - obiektywu i okularu o ogniskowych odpowiednio f1 i f2. Odległość między soczewkami d = f1 + f2. Teleskop Keplera daje obraz odwrócony.
Bieg promieni w teleskopie Keplera:
a) dla przedmiotu umieszczonego w nieskończoności, b) dla przedmiotu w skończonej.
Drugim podstawowym typem teleskopu soczewkowego jest teleskop Galileusza. Teleskop Galileusza składa się z obiektywu S1, którym jest soczewka skupiająca o ogniskowej f1 i okular S2, który tworzy soczewka rozpraszająca o ogniskowej - f2. Teleskop Galileusza daje w odległości dobrego widzenia pozorny, prosty obraz przedmiotu.
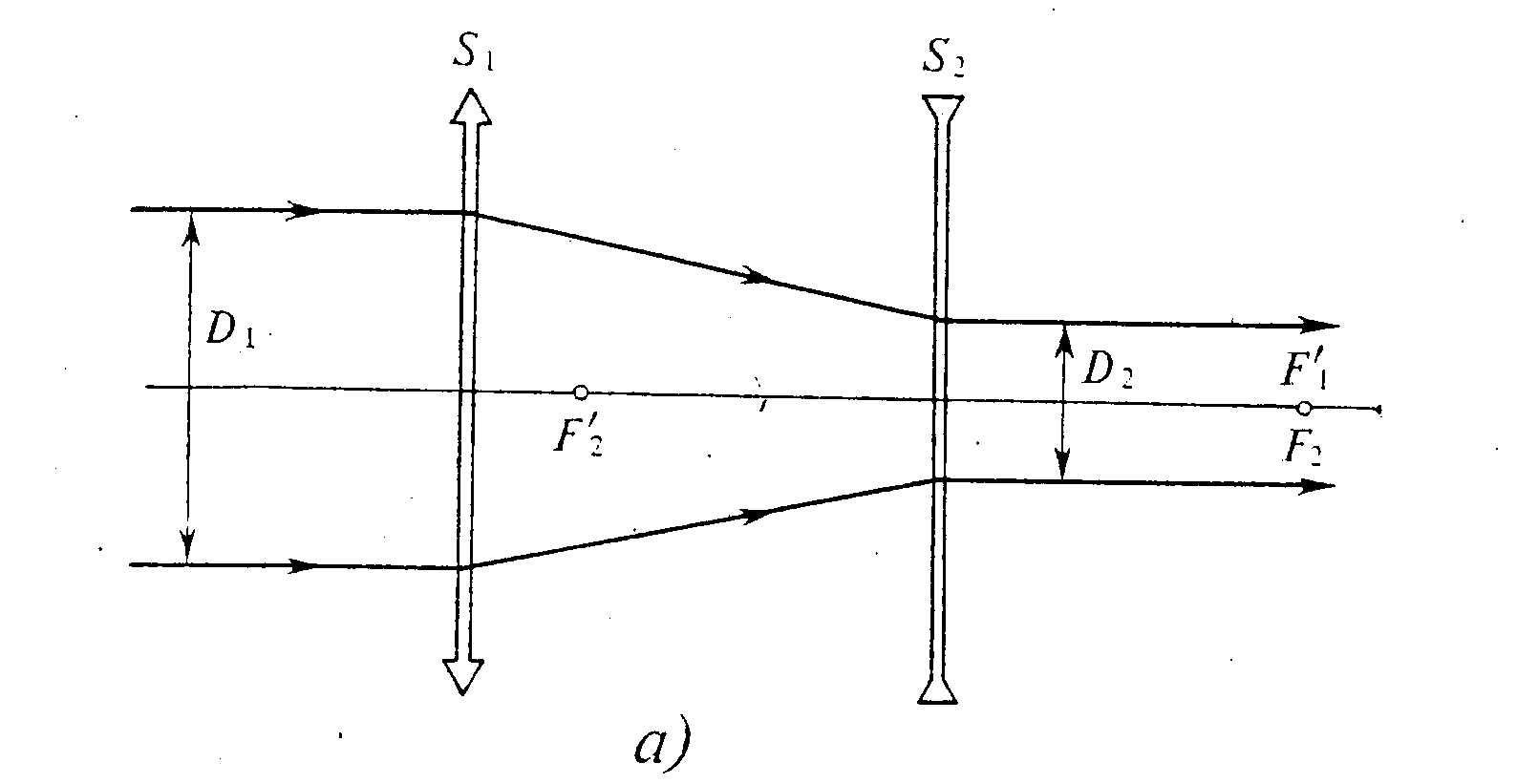
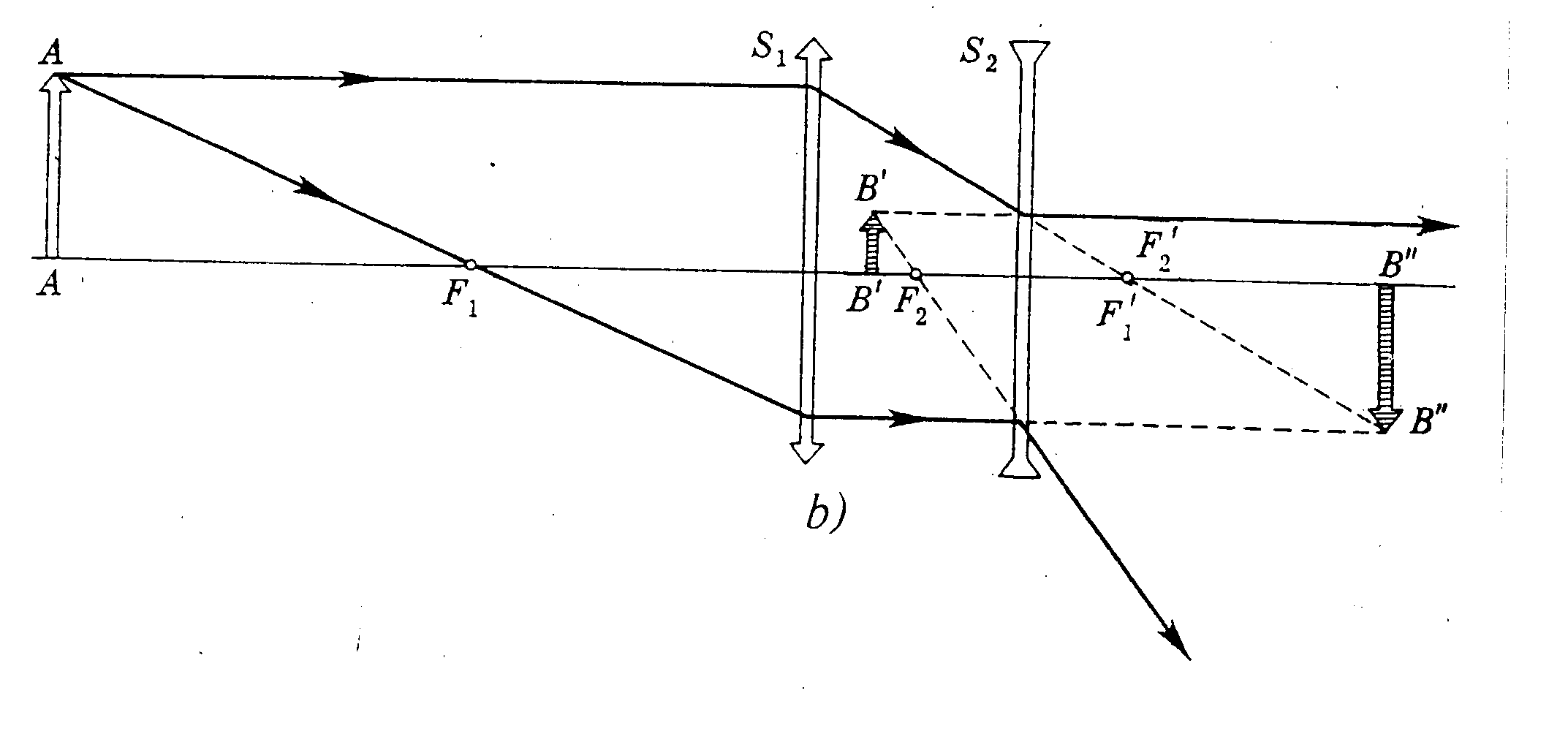
Bieg promieni w teleskopie Galileusza:
a) dla przedmiotu umieszczonego w nieskończoności, b) dla przedmiotu w skończonej
3. Przebieg ćwiczenia:
a) wyznaczanie parametrów teleskopu Keplera:
Ponieważ odległość między soczewkami w teleskopie Keplera powinna byś sumą ich ogniskowych przed przystąpieniem do montażu kładu ogniskowe te zostały zmierzone. Dokładna znajomość tych wartości jest ważna, dlatego, że tylko przy możliwie idealnym ustawieniu soczewek względem siebie można uzyskać po przejściu przez teleskop wiązkę równoległą.
Parametry promienia podczas jego propagacji przez teleskopy Keplera można wyznaczyć, korzystając z macierzy T obliczonej dla propagacji promienia przez układ dwóch cienkich soczewek oddalonych o odległość d.
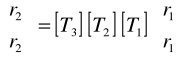
Gdzie Wypadkowa macierz [T] = [T3] [T2] [T1] wynosi:
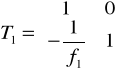
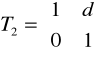
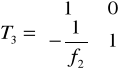
![]()
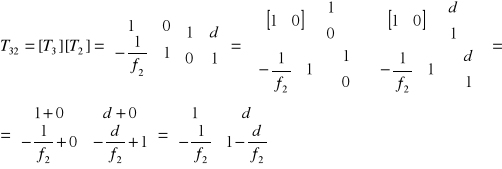
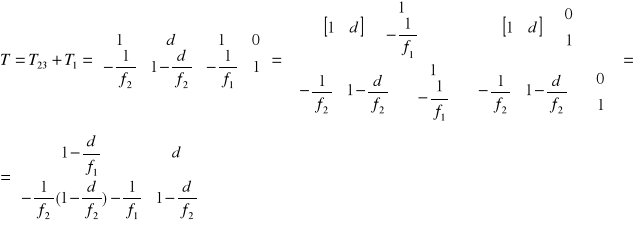
Uwzględniając we wzorze, że d = f1 + f2 dla teleskopu Keplera macierze transmisji przyjmują postać
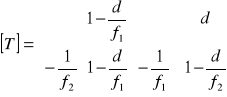
=> 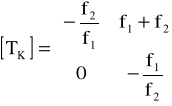
Korzystając z otrzymanej macierzy można zapisać równanie propagacji promienia po przejściu przez teleskop następująco:
![]()
=>
![]()
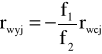
=> ![]()
b) badanie rozbieżności wiązki po przejściu przez teleskop:
W tej części ćwiczenia badaliśmy jak zmienia się rozbieżność promieni po przejściu przez układ soczewek, jeżeli teleskop jest „rozstrojony” tzn., kiedy nie spełnia warunku odległości między soczewkami i odległość ta jest różna od sumy ich ogniskowych. W tym celu zmniejszaliśmy i zwiększaliśmy odległość dzielącą soczewki badając w pewnej odległości od układu zmianę odległości między wiązkami.
Δd |
10 |
8 |
6 |
4 |
2 |
0 |
-2 |
-4 |
-6 |
-8 |
-10 |
2H |
350 |
260 |
200 |
150 |
115 |
100 |
100 |
145 |
205 |
250 |
280 |
h |
166 |
121 |
91 |
66 |
91 |
46 |
41 |
63,5 |
93,5 |
116 |
131 |
D+Δd |
1819 |
1822 |
1825 |
1828 |
1831 |
1834 |
1837 |
1840 |
1843 |
1846 |
1849 |
tg r'wyj |
10,958 |
15,058 |
20,055 |
27,697 |
20,121 |
40,001 |
44,805 |
28,976 |
19,711 |
15,914 |
14,115 |
r'wyj |
79,042 |
74,942 |
69,945 |
62,303 |
69,879 |
0,900 |
45,195 |
61,024 |
70,289 |
74,086 |
75,885 |
4. Wnioski:
Po przeprowadzeniu ćwiczenia i wykonaniu obliczeń doszliśmy do wniosku, że jeżeli w teleskopie Keplera nie jest spełniona zasada odległości (sumy ogniskowych) między soczewkami, to promienie przechodzące przez teleskop przestają być równoległe Na powyższym wykresie zostało zobrazowane zachowanie się wiązki przechodzącej przez teleskop Keplera względem zaburzania odległości miedzy soczewkami (otrzymany wykres jest parabolą, którego minimum wyznacza idealne ustawienie soczewek względem siebie).
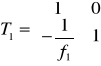
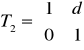
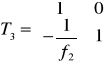
Wyszukiwarka
Podobne podstrony:
opto cw1
Katedra Opto, Optoelektronika
opto test 1 i 2, Optoelektronika
Opto, Elementy optoelekotrniczne, Cel ćwiczenia
Optoelektronika nasze 1
SURDOPED nasze
Matlab cw1 2 zaoczni
optoelektronika02
ćw1 Maszyna turinga
Nasze opracowanie pytań 1 40
Korbutowicz,optoelektronika,Technologia wytwarzania półprzewodnikowych struktur optoelektronicznych
MZ TZrokII cw1(1)
nasze forum 1 2 [2005] hipoterapia i dogoterapia
ćw1
cw1 modelowanie id 122786 Nieznany
więcej podobnych podstron