Akademia Górniczo-Hutnicza

im. Stanisława Staszica

WYDZIAŁ INŻYNIERII MECHANICZNEJ I ROBOTYKI

WYTRZYMAŁOŚĆ MATERIAŁÓW

Praca kontrolna nr IA

Zestaw nr 19

Temat:

Obliczyć główne, centralne momenty bezwładności dla przekroju symetrycznego przedstawionego na rysunku.

Wykonał: Sprawdził:

Szymon Grochal dr inż. Sławomir Badura

Rok II , grupa 18 Data……...……….....

Ocena………..……...

1. Dane do obliczeń

1.1 Charakterystyka geometryczna teownika T 60x60

wg. PN-55/H-93406, rys.1.1.

rys.1.1

1.2 Charakterystyka geometryczna ceownika C 200

wg. PN-59/H-93403, rys.1.2.

rys.1.2

1.3 Charakterystyka geometryczna kątownika L 150x100x10

wg. PN-64/H-93402, rys.1.3.

rys.1.3

2. Obliczanie środka ciężkości profili względem przyjętych osi:

2.1 Układ współrzędnych przyjęty taki jak na rysunku - rys.2.

2.2 Dane potrzebne do obliczenia środka ciężkości.

Teownik	At=7,94 cm^2	yt=-ey-g-et=-4,81cm-0,88cm-1,66cm=-7,35cm
Ceownik	Ac=32,2 cm^2	yc=-ey-ec=-4,81cm-2,01cm=-6,82cm
Kątownik	Al=24,3 cm^2	yl=0

2.3 Obliczanie środka ciężkości profilu (X₀,Y₀) względem układu Oxy, rys.2.

X₀=0 - ponieważ oś Y pokrywa się z osią symetrii przekroju Y_c. Środek ciężkości leży na Y.

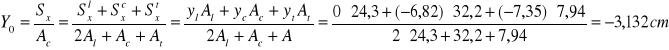
3. Obliczenie głównych centralnych momentów bezwładności względem osi Yc i Xc umieszczonych w środku ciężkości profilu.

3.1 Układ współrzędnych przyjęty taki jak na rysunku - rys.3.

3.2 Dane potrzebne do obliczenia momentów bezwładności względem osi Xc i Yc.

Teownik	Ceownik	Kątownik
Ixt=23,8 cm^4	Ixc=1910 cm^4	Ixl=557 cm^4
Iyt=12,2 cm^4	Iyc=148 cm^4	Iyl=201 cm^4
At=7,94 cm^2	Ac=32,2 cm^2	Al=24,3 cm^2
y0t=yt+3,132 cm=-4,218 cm	y0c=yc+3,132 cm=-3,688 cm	y0l=3,132 cm
x0t=0	x0c=0	x0l=ex+0,5=2,85 cm

Ponieważ ceownik został obrócony względem rysunku normowego, oś yc ceownika stała się równoległa do osi Xc obliczanego przekroju, tym samym w obliczeniach Ix uwzględniane jest Iyc nie Ixc.

3.3 Obliczanie momentów bezwładności względem osi Xc i Yc dla całkowitego przekroju z wykorzystaniem wzoru Steinera, rys.3.

- Wzór Steinera

Ix=Ixc+a²A Ixc,Iyc - moment bezwładności względem środka ciężkości

Iy=Iyc+b²A a,b - odległości między osiami A - pole powierzchni przekroju

Ix=2Ix_lc+Ix_cc+Ix_tc=2[Ixl+y0l²A_l]+Iyc+y0c²A_c+Ixt+y0t²A_t=2[557+(3,132)² 24,3]+148+

+(-3,688)² 32,2+23,8+(-4,218)² 7,94=2341,7659 cm⁴

Iy=2Iy_lc+Iy_cc+Iy_tc=2[Iyl+(x0l)²A_l]+Ixc+Iyt=2[201+(2,85)² 24,3]+1910+12,2=2718,9535 cm⁴

Symbol	Wielkość
h	60 mm
s	60 mm
g	7 mm
t	7 mm
A	7,94 cm^2
Ix	23,8 cm^4
Iy	12,2 cm^4
e	1,66 cm

Symbol	Wielkość
h	200 mm
s	75 mm
g	8,8 mm
t	11,5 mm
A	32,2 cm^2
Ix	1910 cm^4
Iy	148 cm^4
e	2,01 cm

Symbol	Wielkość
h	150 mm
s	100 mm
g	10 mm
A	24,3 cm^2
Ix	557 cm^4
Iy	201 cm^4
ex	2,35 cm
ey	4,81 cm

rys.2 Przekrój symetryczny profili z naniesionym układem Oxy, względem którego obliczany jest środek ciężkości.

rys.3 Przekrój symetryczny profili z naniesionym układem OXcYc, umieszczonym w środku ciężkości profilu całkowitego

---