Para sił.
Linie działania dwóch sił mogą zajmować względem siebie różne położenia w przestrzeni. Mogą się pokrywać, przecinać, być równoległe lub żuchrowate.
Jeżeli linie działania się pokrywają, czyli dwie siły działają wzdłuż jednej prostej to przy równych modułach i przeciwnych zwrotach są równoważne zeru , w przeciwnym razie dają się sprowadzić do wypadkowej.
Podstawowe własności pary sił.
1. dwie pary sił leżące w tej samej płaszczyźnie są równoważne gdy mają równe momenty.
P![]()
h ![]()
═ P ![]()
h ![]()
h ![]()
P ![]()
P![]()
h ![]()
P![]()
Twierdzenie o trzech siłach.
W wielu przypadkach ciało sztywne jest w równowadze pod działaniem trzech nierównoległych sił leżących w jednej płaszczyźnie. Wtedy w rozwiązywaniu zagadnień praktycznych jest pomocne tzw. twierdzenie o trzech siłach.
,,jeżeli ciało sztywne jest w równowadze pod działaniem trzech nierównoległych sił leżących w jednej płaszczyźnie, to linie działania tych sił muszą przecinać się w jednym punkcie, a siły tworzy układ zamknięty.
P![]()
P ![]()
P![]()
P ![]()
P ![]()
Zasada zesztywnienia.
Równowaga sił działania na ciało uzyskał dno nie zmieni się przez zesztywnienie tego ciała.
Zasada akcji i reakcji.
Każdemu działaniu towarzyszy równe co w wartości działanie wydłuż tej samej prostej przeciwdziałanie.
1 ‾ R A
R
Zasada oswabadzania odwięzów.
Ciało swobodne ma 6 stopni swobody (3 kierunki, 3 osie obwodu).
Rodzaje więzów.
- cięgno- element wiotki rozciągalny ( nitki) nie gnący.
A
G - pręty przegubowe- przenosi siły
Wzdłuż osi, siły rozciągamy i ściąga-
my
- podpora- przegub( obciążenia w je-
dnej płaszczyźnie, kulisty- przestrze-
nny).
Podpora
( reakcja prostopadła do
płaszczyzny
- zamurowanie-
R![]()
P
M![]()
-płaski układ sił zbieżnych
W═ P![]()
+ P![]()
+ P ![]()
+P ![]()
P![]()
P
P![]()
P ![]()
Równowaga układu płaskiego sił
Zbieżnych W═O(zamknięty wielobok
`
Jeżeli na dane ciało działa układ 3 sił
nierównoległych działających w
jednej płaszczyźnie i ciało to znajduje
się w równowadze to linie działania
tych sił muszą przecinać się w 1
punkcie A same siły muszą tworzyć
zamknięty trójkąt sił. P
P ![]()
P![]()
P![]()
P ![]()
C
P
α ═ 60º
A
R
P
P![]()
2
1 P
1 2
P![]()
Y
1
1
P P
1 X
Y
X
W![]()
═ P![]()
![]()
+ P![]()
![]()
+ P ![]()
![]()
W![]()
═ P![]()
![]()
+ P![]()
![]()
+.... + P![]()
![]()
W![]()
═ ![]()
P![]()
![]()
W![]()
═ ![]()
P![]()
![]()
W ═ O Równowaga
W![]()
═ ![]()
P![]()
![]()
═
W![]()
═ ![]()
P![]()
![]()
TARCIE.
G N═ G
FF
N
Tarcie całkowite rozwinięte
N
Tg α ═ ![]()
- Czynnik tarcia═ μ
siła tarcia może zmieniać się od O do wartości maksymalnej zwanej tarciem całkowitym rozwiniętym,
siła tarcia nie zależy od wielkości stykających się powierzchni a tylko od ich stanu.
Suma rzutów na osi x═ 0
Zp ![]()
═ 0 ═ P* T T ═ μ N
Suma rzutów na osi y ═ 0
Zp![]()
═ 0 ═ N*G
y
G
P
x
N
α
φ
φ
T dla P![]()
P N
α
P![]()
═ ?
Zp ![]()
═ 0 ═ P+T - φ sin α
Zp![]()
═ 0 ═ N- φ cos α
T ═ μ N
P ![]()
═ ?
Zp ![]()
═ 0 ═ P-T - φ sin α
Zp![]()
═ 0 ═ N- φ cos α
T ═ μ N
Moment siły względem punktu.
Nazywamy iloczyn wartości liczbowej tej siły najkrótszej odległości punktu od linii działania siły - ramie siły.
E B
P
M ujemny gdy ruch zgodny ze wskazówkami zegara,
M Dodatnie gdy ruch przeciwny do ruchu wskazówek zegara.
M![]()
═ Ph
M ![]()
═ Ph ![]()
Para sił.
Parą sił nazywamy dwie siły równe co do wartości, przeciwnie skierowane, działające wzdłuż prostych równoległych przesuniętych o pewną odległość.
P
h P![]()
P ═ P![]()
M ═ P ○ h
Równy iloczynowi wartości jednej z sił,
I odległością działania sił ich liniami.
A
P
h
0![]()
P
B
M ═ P ○ h
M ![]()
═ P A0![]()
+ PO![]()
B═
P(A0![]()
+ O![]()
B)
M ![]()
═ P AO ![]()
- + PBO ![]()
═
P(AO ![]()
- BO ![]()
)
P ○ h P![]()
○ h ![]()
P P![]()
h h ![]()
P
P![]()
Jeżeli na płaszczyznę działa n par
sił to można je zastąpić parą
wypadkową sił której moment
jest równy algebraicznej sumie
momentów tych par składowych.
Twierdzenie Varignon'a.
Moment wypadkowy względem
dowolnego punktu na
płaszczyznę jest równy sumie
momentów sił składowych
względem tego samego punktu.
y
P
A
y
h
x
0 x
M![]()
═ P*h
P![]()
*y + P![]()
*x ═ P ![]()
![]()
y+
P ![]()
![]()
x ═ P( y sin ![]()
+
X cos ![]()
)
P
A
B
h
a
płaski, dowolny, układ sił
B
A
C
D
W ═ P![]()
+ P ![]()
+ P ![]()
+ P![]()
...
+P![]()
M ═ M![]()
+ M![]()
+ M![]()
+M![]()
+
…+ M![]()
Warunek równowagi
W ═ P![]()
+ P ![]()
+ P ![]()
+ P═ 0
M═ 0
W
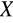
═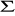
P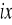
═0W
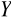
═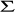
Pi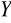
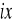
═0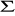
M
═0
Opór tarcia.
- tarcie pos
Podaj definicje pary sił i udowodnij
że jej moment jest jednakowy wzglę
dem dowolnego punktu na płaszczy
źnie.
Para sił - dwie siły równe co do wartości przeciwnie skierowane działają wzdłuż prostych przesuniętych o pewną odległość.
P ═ P ![]()
P
x
P ![]()
h
moment jest stały I równe są iloczynowi wartości jednej z sił między liniami działania sił.
N ═ P*h
Wyszukiwarka
Podobne podstrony:
WYTRZYMAOsc sciga, inżynieria ochrony środowiska kalisz, a pwsz kalisz ioś, IV mechanika i wytrzymał
Zasady statyki wizy i ich reakcje-cigag, inżynieria ochrony środowiska kalisz, a pwsz kalisz ioś, IV
TEMATY EGZAMINACYJNE Z PBU pwsz ioś kalisz, inżynieria ochrony środowiska kalisz, a pwsz kalisz ioś,
Projekt 09, inżynieria ochrony środowiska kalisz, a pwsz kalisz ioś, IV odpady i wytrzymalosc materi
Projekt 07, inżynieria ochrony środowiska kalisz, a pwsz kalisz ioś, IV odpady i wytrzymalosc materi
Projekt 005, inżynieria ochrony środowiska kalisz, a pwsz kalisz ioś, IV odpady i wytrzymalosc mater
Projekt 03, inżynieria ochrony środowiska kalisz, a pwsz kalisz ioś, IV odpady i wytrzymalosc materi
Projekt 04, inżynieria ochrony środowiska kalisz, a pwsz kalisz ioś, IV odpady i wytrzymalosc materi
Projekt 02, inżynieria ochrony środowiska kalisz, a pwsz kalisz ioś, IV odpady i wytrzymalosc materi
Projekt 01, inżynieria ochrony środowiska kalisz, a pwsz kalisz ioś, IV odpady i wytrzymalosc materi
W-14, inżynieria ochrony środowiska kalisz, a pwsz kalisz ioś, Meteorologia materialy
W-10, inżynieria ochrony środowiska kalisz, a pwsz kalisz ioś, Meteorologia materialy
W-06, inżynieria ochrony środowiska kalisz, a pwsz kalisz ioś, Meteorologia materialy
więcej podobnych podstron