Wskaźniki regresji
Korelacja
Zależność liniowa pomiędzy dwoma cechami.
Jeżeli średnim wartościom jednej cechy towarzyszą zmiany średniej wartości drugiej cechy to mówimy o zależności korelacyjnej.
Korelacja dzieli się na:
Dodatnia
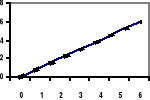
Ujemna
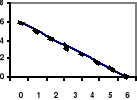
Brak korelacji liniowej
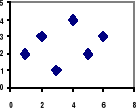
Do badania siły związku między dwiema cechami służy współczynnik zależności Pearsona:
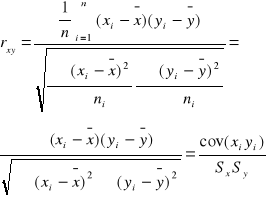
rxy (-1,1)
rxy <0,2 - brak zależności liniowej
rxy 0,2-0,4 - zależność liniowa wyraźna, lecz niska
rxy 0,4-0,7 - zależność umiarkowana
rxy 0,7-0,9 - zależność znacząca
rxy >0,9 - zależność silna
Liniowe równanie regresji:
![]()
- pokazuje jak zmienia się zmienna y jeśli zmienna x zmieni się o 1 jednostkę
ay - współczynnik kierunkowy równania regresji i mówi nam, co się dzieje ze zmienną zależną y, jeśli zmienna niezależna x zmieni się o 1 jednostkę
by - jest wyrazem wolnym równania i nie ma interpretacji ekonomicznej
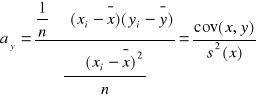
![]()
![]()
![]()
- pokazuje jak zmienia się zmienna x jeśli zmienna y zmieni się o 1 jednostkę
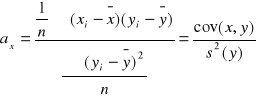
![]()
![]()
![]()
Współczynnik determinacji
![]()
- mówi nam w jakim procencie zmiany jednej cechy są wyjaśnione zmianami drugiej cechy
Wnioskowanie statystyczne
Zmienna losowa - zmienna, której wartości nie można z góry przewidzieć, czyli przyjmuje wartości z określonymi prawdopodobieństwami.
Zbiór wartości zmiennej losowej jest jednoznacznie określony
Zmienne losowe dzieli się na:
Zmienna skokowa
Zmienna ciągła
x1, x2, x3,..., xn - wartości zmiennej
X - zmienna losowa typu skokowego
p - prawdopodobieństwo odpowiadające określonej zmiennej
![]()
- gdy zmienna losowa przyjmuje wartości skończone
![]()
gdy zmienna losowa przyjmuje wartości nieskończone
Rozkład zmiennej losowej, czyli jej wartościom i odpowiadające im prawdopodobieństwo można określić za pomocą funkcji prawdopodobieństwa lub dystrybuanty.
Def. 1
Funkcją prawdopodobieństwa zmiennej losowej skokowej X, która przyjmuje wartości xi (i=1, n) jest prawdopodobieństwo, że zmienna losowa przyjmie prawdopodobieństwo P(x=xi)=pi
Argumentami f. prawdopodobieństwa są wartości zmiennej losowej, natomiast wartościami funkcji są prawdopodobieństwa realizacji poszczególnych wartości zmiennej losowej:
x1 |
x2 |
x3 |
x4 |
x5 |
xn |
p1 |
p2 |
p3 |
p4 |
p5 |
pn |
Def. 2
Dystrybuantą zmiennej losowej X, nazywamy funkcję f(x) określoną na zbiorze liczb rzeczywistych mianowicie F(x)=P(X<x). Ta definicja odnosi się zarówno do zmiennych losowych skokowych jak i ciągłych. Zapis ten oznacza zmienna losową X przyjmującą wartości równe prawdopodobieństwu tego, że ta zmienna osiąga wartości nie większe od wartości argumentu.
Przykład
Przy rzucie kostką przyporządkujemy średniej losowej X wyrzucone liczby oczek od 1 do 6.
![]()
- nie istnieje żadna wartość rozważanej zmiennej losowej, która mogłaby się pojawić z prawdopodobieństwem dodatnim
F(X)=P(x<0)=0
![]()
: F(X)=P(X<1)=0
![]()
: F(X)=P(X<2)=1/6 - ponieważ można zaobserwować wartość x=1 z prawdopodobieństwem 1/6.
![]()
: F(X)=P(X<3)=2/6
![]()
: F(X)=P(X<6)=5/6
Dystrybuantę rozpatrywanej zmiennej losowej można przedstawić jako:
0 dla ![]()
P1 dla ![]()
P1 + P2 dla ![]()
F(x)
. . . .
P1+P2+P3+Pn-1 dla ![]()
1 dla![]()
Z powyższego zapisu widzimy, ze dystrybuanta przyjmuje wartości z przedziału <0,1>, że w granicy ![]()
a w ![]()
oraz, że dystrybuanta jest funkcją niemalejącą![]()
zachodzi ![]()
, a także, że dystrybuanta jest funkcja prawostronnie ciągłą.
Jeżeli x przyjmuje wartości x1,x2,x3,..., xn odpowiednio z przedziału pi(i=1,...n) to:
![]()
Jak mamy wyznaczyć prawdopodobieństwo ![]()
. To możemy przedstawić jako różnicę:
![]()
![]()
Def. 3
Funkcją gęstości prawdopodobieństwa zmiennej losowej ciągłej nazywamy funkcję F(x) określoną na zbiorze liczb rzeczywistych o następujących własnościach ![]()
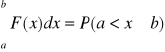
dla a<b
Z tej własności wynika, że funkcja gęstości spełnia warunek:
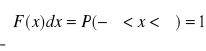
Zauważmy, ze prawdopodobieństwo postaci P(X=a), gdzie „a” jest ustalona wartością zmiennej losowej ciągłej, na podstawie def. 3 jest równa .
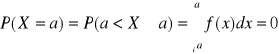
Rozkład dwumianowy (Bernoulliego)
Wykazujemy doświadczenie, którego rezultatem może być pewne zdarzenie A, występujące z prawdopodobieństwem p lub zdarzenie do niego przeciwne, które może pojawić się z prawdopodobieństwem (1-p)=q. Jedno z tych zdarzeń np. A określa się jako sukces, drugie natomiast - jako porażkę. Doświadczenie to powtarzamy n-krotnie w sposób niezależny tzn. wynik uzyskany w poprzednim doświadczeniu nie wpływa na wynik drugiego doświadczenia, czyli innymi słowy prawdopodobieństwo sukcesu jest w poszczególnych próbach stałe i równe p. Liczba sukcesów jaka zaobserwujemy w wyniku n-krotnego powtórzenia doświadczenia może być równa k=0,1,2,3,..
Przykład
Rzucamy 10 razy monetą. W pojedynczym rzucie można wyrzucić orła (sukces) z prawdopodobieństwem ½. Orzeł może wypaść k=0,1,2,3,..,100. Niech zmienna losowa X będzie liczbą sukcesów zaobserwowanych w eksperymencie przeprowadzonym zgodnie ze schematem Bernoulliego. Jest to zatem zmienna losowa skokowa przyjmująca wartości k=(0,1,2,3,..n). Wyznaczymy dla niej funkcję prawdopodobieństwa, czyli P(X=k) dla k=0,1,2,3...n. Zdarzenie X=k zachodzi wtedy, gdy w wyniku n-krotnego powtórzenia pojedynczego doświadczenia zaobserwujemy dowolny ciąg zdarzeń, w którym pojawiło się ![]()
(sukces) oraz ![]()
(porażka)
Prawdopodobieństwo otrzymania w eksperymencie takiego ciągu zdarzeń jest różne ze względu na niezależność pojedynczych doświadczeń iloczynowi prawdopodobieństw poszczególnych n-zdarzeń, czyli ![]()
.
Liczba różnych możliwych ciągów n-elementowych, których zdarzenie A występuje k-razy jest równa liczbie kombinacji z n-elementów po k, czyli ![]()
Wszystkie te kombinacje składają się na zdarzenie, że zmienna losowa X przyjmie wartości k, a zatem jego prawdopodobieństwo jest suma prawdopodobieństw dla poszczególnych kombinacji:
![]()
Def. 4
Zmienna losowa X ma rozkład dwumianowy (Bernoulliego), jeżeli przyjmuje wartości k=0,1,2,3,...n z prawdopodobieństwami określonymi wzorem p(X=k)=...
Liczbą doświadczeń n oraz prawdopodobieństwem sukcesu p nazywamy parametrami rozkładu dwumianowego.
Dystrybuanta zmiennej losowej X o rozkładzie dwumianowym wyraża się następującym wzorem:
![]()
E(x)=np. - wartość oczekiwana
b2(x)=np.(1-p)=npq - wariacja
Wartość oczekiwana - oczekiwana liczba sukcesów w n-doświadczeniach, ta wartość jest równa iloczynowi liczby doświadczeń i prawdopodobieństwa realizacji sukcesu w pojedynczym doświadczeniu
Rozkład Poisson'a
Za pomocą tego rozkładu można w sposób przyblizony opisywać, charakteryzować takie zjawiska jak liczba usterek, pojawiająca się w produkcji danego dobra liczba zgłoszeń szkód ubezpieczeniowych, liczba błędów drukarskich, dostępność sieci przesyłowych
Def. 5
Zmienna losowa X przyjmująca wartości k=0,1,2,3,...ma rozkład Poisson'a o parametrze ![]()
(lambda) jeżeli jej funkcja prawdopodobieństwa określona jest wzorem ![]()
k=0,1,2,3...
Dystrybuantą tego rozkładu jest sumą![]()
![]()
![]()
Przykład
Stwierdzono, że w pewnym składzie książek popełniono przeciętnie 1,5 błędu na stronę. Z dokładnością 0,001 podamy prawdopodobieństwo wystąpienia 0,1,2,3... błędów na stronie. Przyjmując w założeniu, że rozpatrywana zmienna losowa ma rozkład Poisson'a.
X liczba błedów na stronie
E(x) - 1,5 ![]()
![]()
![]()
.
.
.
![]()
Na podstawie powyższego wzoru uzyskujemy określone prawdopodobieństwo.
Rozkład normalny (rozkład zmiennej ciągłej)
Zjawiska podlegające rozkładowi normalnemu: waga, wzrost, losowe pomiary błędów.
Do rozkładu normalnego prowadzi taki proces kształtowania zjawiska, w ramach którego na to zjawisko oddziałuje bardzo duża liczba czynników niezależnych, których wpływ indywidualny jest nieznaczny.
Prawo rozkładu normalnego podlega wpływowi wielu jednocześnie działających czynników.
Formalne uzasadnienie dla normalnego rozkładu zjawiska na gruncie rachunku prawdopodobieństwa dostarcza tzw. centralne twierdzenie graniczne.
Def. 6
Zmienna losowa x ma rozkład normalny o parametrach ![]()
, co w skrócie oznacza ![]()
, gdzie
m - wartość parametru,![]()
(sigma)- odchylenie standardowe, jeśli jej funkcja gęstości ma postać:
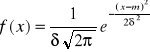
Funkcja gęstości rozkładu normalnego z parametrami m i ![]()
ma graficzną postać:
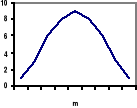
Dystrybuanta tego rozkładu ma postać: 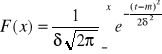
E(x)=m
b2(x)=![]()
Krzywa gęstości rozkładu normalnego ma następujące własności:
Jest symetryczna względem prostej x=m
Osiąga maksimum w
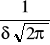
dla x=mramiona krzywej gęstości mają punkty przegięcia dla
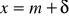
oraz dla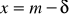
Jeśli mamy P(a<x<b) dla a<b i dowolne parametry m i ![]()
uciekamy się do rozkładu normalnego standaryzowanego, którego funkcja gęstości i dystrybuanta zostały stablicowane.
Dowodzi się, że jeżeli zmienna losowa ma rozkład normalny ![]()
to zmienna standaryzowana ![]()
ma rozkład normalny o parametrach N(0,1)
Def. 7
Rozkład normalny z parametrami N(0,1) nazywamy rozkładem normalnym.
Schemat obliczania:
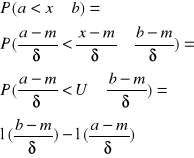
Wartość dystrybuanty odczytujemy z tablic dystrybuant ze standardowego rozkładu normalnego.
Przykład
Zakładamy, ze zmienna losowa x ma rozkład normalny N(m,![]()
). Mamy obliczyć prawdopodobieństwo, że zmienna losowa x przyjmie wartości różniące się od średniej m nie więcej niż o:
1 odchylenie standardowe
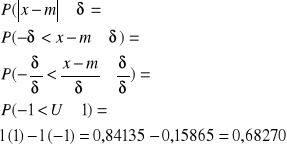
Wartość zmiennej x różnić się będzie od średniej m o nie więcej niż o jedno odchylenie standardowe.
2 odchylenie standardowe
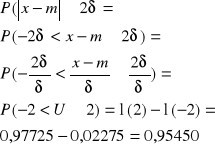
3 odchylenia standardowe
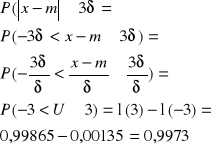
Reguła 3 sigm
Jeżeli wartość zmiennej losowej ciągłej przekracza trzykrotna wartość odchylenia standardowego, to wartość nie ma znaczenia poznawczego (należy je pominąć). Tylko odchylenia nie przekraczające trzykrotnego odchylenia standardowego są brane pod uwagę.
Przykład
Zmienna losowa X ma rozkład normalny N(5,2). Należy obliczyć prawdopodobieństwo, że zmienna przyjmuje wartości z przedziału (P(3<X<7)
![]()
![]()
![]()
- ze względu na symetrię funkcji gęstości rozkładu normalnego względem wartości średniej, której U jest równe 0, można dokonać następującego przekształcenia:
![]()
![]()
- z takim prawdopodobieństwem zmienna będzie przyjmowała wartości z przedziału 3<X<7.
Podstawy wnioskowania statystycznego dotyczące rozkładów jednorodnych
Aby wyjaśnić pojęcie próby losowej rozpatrujemy sytuację:
Wykonujemy serię doświadczeń, polegających na rzucie kostką, obserwując liczbę wyrzucanych oczek. Załóżmy, że uzyskaliśmy wyniki które zawiera tabela:
Numer kolejny doświadczenia |
x1 |
x2 |
x3 |
x4 |
1 |
5 |
5 |
4 |
1 |
2 |
1 |
1 |
5 |
6 |
3 |
3 |
1 |
3 |
6 |
4 |
3 |
2 |
5 |
1 |
5 |
5 |
2 |
4 |
2 |
6 |
4 |
6 |
3 |
4 |
Badana zmienna losowa X (liczba wyrzuconych oczek) ma w populacji generalnej rozkład określony prawdopodobieństwami jednakowymi![]()
. Z tej populacji pobrano serię 4 elementowych prób, których wyniki zapisywaliśmy za każdym razem jako ciągi w postaci x1, x2, x3, x4, gdzie każdy x oznacza liczbę wyrzucanych oczek w kolejnych 4 rzutach. Zauważmy, że wyniki pierwszego rzutu krostką można traktować jako realizację zmiennej losowej, którą możemy oznaczyć X1.Zmienna losowa X1 (wyniki pierwszego rzutu) ma taki sam rozkład jak zmienna losowa X (wynik rzutu kostką). Podobne wyniki 2, 3 i 4 rzutu można traktować jako realizację zmiennych losowych, które oznaczymy odpowiednio X2, X3, X4. Zmienne te mają jednakowe rozkłady, takie jak rozkład zmiennej losowej X. W rozpatrywanym przykładzie próbą losową (w sensie matematycznym) tworzy ciąg zmiennych losowych (X1, X2, X3, X4). Z charakteru doświadczenia wynika ponadto, ze te zmienne są zmiennymi niezależnymi, tzn. że realizacja jednej z nich nie zależy od realizacji pozostałych. W takim przypadku próbę losową określamy jako próbę prostą.
Def. 8
Próbą losową prostą jest ciąg zmiennych losowych (X1, X2....Xn) niezależnych mających jednakowe rozkłady takie, jak rozkład zmiennej losowej X populacji.
Konkretna próba losowa jest to n-elementowy ciąg (x1, x2...xn) określony mianem przestrzeni próby losowej (X1, X2..Xn). W omawianym wyżej przykładzie przestrzeń próby losowej składa się z 64 elementów.
Statystyka z próby i jej rozkład
Statystyką z próby nazywamy zmienną losową Zn, będącą funkcją zmiennych (X1, X2...Xn) stanowiących próbę losową. Owymi statystykami mogą być np. wartości średniej, wariacja.
Dla konkretnych prób określona statystyka będzie przyjmowała na ogół różne wartości. Statystyka jako funkcja zmiennych losowych sama jest przeto zmienną losową, a w związku z tym ma określony rozkład.
Rozkład statystyki ![]()
nazywamy rozkładem próby. Zależy on od rozkładu zmiennej losowej X populacji generalnej oraz od liczebności próby.
Wyróżniamy dokładne rozkłady statystyk z próby przy ustalonym n i wykorzystuje się te rozkłady wówczas, gdy mamy do czynienia z małymi próbami. Za małą próbę uznaje się próbę, której liczba elementów jest mniejsza od 30. Dla dużych prób wykorzystuje się tzw. rozkłady graniczne.
Rozkład średniej arytmetycznej z próby dla populacji o rozkładzie normalnym
Załóżmy, ze cecha X ma w populacji generalnej rozkład normalny ![]()
. Z tej populacji pobieramy próbę losową n-elementową. Można wykazać, ze przy powyższych założeniach średnia arytmetyczna z próby![]()
ma na mocy własności addytywności rozkładu normalnego rozkład normalny ze średnią ![]()
i odchyleniem standardowym ![]()
, gdzie ![]()
Własności addytywności rozkładu normalnego
Niech X1 i X2 będą niezależnymi zmiennymi losowymi o rozkładach ![]()
i ![]()
. Dowodzi się, ze zmienna losowa będąca sumą zmiennych X1 i X2 ma również rozkład normalny ![]()
Obserwuje się 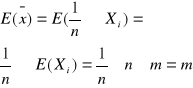
, a zatem wartość oczekiwana średniej z próby (średnie z możliwych średnich prób) jest równa średniej interesującej nas zmiennej losowej w populacji generalnej.
Ponieważ zmienne losowe (X1, X2...Xn) tworzące próbę są niezależne to na podstawie zależności ![]()
oraz ![]()
otrzymujemy, że 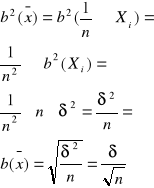
Rozproszenie wartości średniej z prób jest zależne od wielkości próby. W raz ze wzrostem liczebności próby owo rozproszenie maleje.
Rozkład t-studenta i rozkład ![]()
(chi kwadrat) na przykładzie rozkładu średniej arytmetycznej z próby normalnej z nieznanym odchyleniem standardowym ![]()
.
Zakładamy, że zmienna losowa ma rozkład normalny ![]()
. Rozkład średniej arytmetycznej z próby jest zależny od wartości obu parametrów. Rozkładu zmiennej losowej X populacji. .Jeżeli wartość odchylenia![]()
jest nieznana to zdarza się często, że parametry rozkładu średniej arytmetycznej nie mogą być wyznaczone o wyżej przeprowadzone rozważania.. Wówczas do wnioskowania o średniej m wykorzystuje się następującą statystykę:
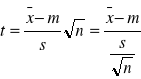
t - zmienna losowa
n - liczebność populacji
s - odchylenie standardowe
Rozkład zmiennej t zwany rozkładem t-studenta za n -1 stopniami swobody jest niezależny od parametru ![]()
.
Stopnie swobody są parametrami rozkładu zmiennej t ściśle związanymi z liczebnością próby. Liczba stopni swobody jest tutaj równa liczbie niezależnych obserwacji określających wyższa statystykę.
Ponieważ zachodzi warunek![]()
,dlatego liczba niezależnych obserwacji wynosi n -1. Rozkład t-studenta jest rozkładem stablicowanym, przy czym dla n>30 może być ten rozkład z dobrym przybliżeniem zastąpiony rozkładem normalnym. Znalezienie rozkładu wariancji z próby jest zadaniem skomplikowanym. Okazuje się jednak, ze jeżeli populacja generalna ma rozkład normalny z dowolną wartością średnią i wariancją ![]()
, wówczas zmienna ![]()
zdefiniowana w sposób następujący ![]()
ma ustalony rozkład zwany rozkładem ![]()
z n -1 stopniami swobody. Ten rozkład jest również stablicowany, a dla n>30 rozkład ten można przybliżać z dużą dokładnością rozkładem normalnym.
Pewna zmienna losowa ![]()
ma rozkład zmierzający do rozkładu normalnego z parametrami N(0,1). Udowadnia się w statystyce, ze wartość oczekiwana E i odchylenie standardowe D statystyki t są równe:
![]()
![]()
.
Podstawy teorii estymacji
Estymacja - szacowanie, czyli wyznaczanie wartości parametrów rozkładu zmiennej losowej z określonym prawdopodobieństwem (z ograniczona dokładnością).
Podstawowym działem wnioskowania statystycznego jest teoria estymacji zawierająca zbiór metod pozwalających na wnioskowanie o postaci rozkładu populacji generalnej (tzn. o wartości parametrów rozkładu lub rodzaju funkcji rozkładu) na podstawie obserwacji uzyskanej w próbie. Wyróżniamy:
estymację parametryczną - w tym przypadku szacuje się tylko wartości parametrów rozkładu populacji generalnej
estymację nieparametryczną - gdy szacowaniu podlega postać funkcyjna parametrów rozkładu populacji generalnej
W odniesieniu do estymacji parametrycznej możemy mówić o estymacji punktowej i estymacji przedziałowej w zależności od sposobu w jaki dokonujemy szacunku wartości parametrów. W estymacji punktowej jako ocenę wartości parametrów przyjmuje się jedna konkretną wartość (liczbę) na podstawie wyników próby. W estymacji przedziałowej wyznacza się pewien przedział liczbowy, który z określonym prawdopodobieństwem przyjętym z góry pokrywa wartość szacowanego parametru.
Załóżmy, ze rozkład zmiennej losowej X populacji generalnej jest opisany za pomocą dystrybuanty ![]()
, gdzie ![]()
(theta), od którego zależy dystrybuanta, jest parametrem rozkładu. Nieznaną wartość parametru ![]()
szacujemy na podstawie n-elementowej próby. Podstawowym narzędziem estymacji jest estymator.
Estymatorem ![]()
parametru ![]()
populacji generalnej nazywamy statystykę próby (X1, X2 ...Xn), która służy do oszacowania wartości tego parametru.
Estymator jest zmienną losową, a więc ma określony rozkład z odpowiednimi parametrami. Rozkład estymatora ![]()
jest zależny od rozkładu zmiennej losowej X populacji generalnej oraz zależny od parametru ![]()
.
Konkretna wartość liczbową ![]()
jaką przyjmuje estymator ![]()
parametru dla realizacji próby ![]()
nazywamy ocenę parametru ![]()
, a zatem ocena ta jest realizacją zmiennej losowej ![]()
. Ponieważ szacunku parametru dokonuje się na podstawie próby losowej, istnieje możliwość popełnienia błędu. Różnica między wartością estymatora ![]()
a wartością parametru nazywamy błędem estymacji (jest on zmienna losowa) a jako miarę tego błędu przyjmuje się: ![]()
.
Jeżeli wartość oczekiwana![]()
jest równa szacowanemu parametrowi ![]()
to wyrażenie to jest wariancją estymatora ![]()
, czyli![]()
, wtedy odchylenie standardowe ![]()
nazywamy standardowym błędem szacunkowym parametru![]()
.
![]()
- względny błąd szacunku
Właściwości dobrego estymatora:
Estymator powinien być nieobciążony
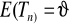
. Jeżeli estymator jest nieobciążony, to uzyskiwane oceny parametrów nie są obciążone błędem systematycznym, np. średnia arytmetyczna jest nieobciążonym estymatorem wartości oczekiwanej w rozkładzie populacji generalnej.Estymator
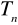
parametru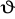
jest zgodny, jeżeli spełnia warunek:
![]()
gdzie ![]()
. To znaczy że dla dużych prób estymator zgodny jest estymatorem, który szacowany parametr wyznacza z maksymalną dokładnością.
Estymator
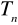
parametru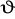
jest nieobciążony, jeżeli jego wariancja spełnia zależność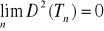
, to estymator jest jednocześnie zgodny. Ponieważ może istnieć wiele nieobciążonych estymatorów parametru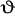
powstaje pytanie wyboru najlepszego z nich. Rozsądny jest wówczas wybór takiego estymatora, który charakteryzuje się najmniejszym rozrzutem wartości w stosunku do wartości parametru. Dlatego z najlepszy estymator uznamy taki, który ma najmniejsza wariancję.
Hipotezy statystyczne i ich weryfikacja
Hipoteza statystyczna - jest to przypuszczenie dotyczące rozkładu populacji generalnej. Wyróżniamy:
Hipotezy parametryczne - to hipotezy precyzujące (określające) wartości parametru w rozkładzie populacji generalnej znanego typu.
Hipotezy nieparametryczne - precyzuje typ rozkładu populacji generalnej
Hipoteza zerowa (
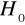
) - jest to podstawowa hipoteza zweryfikowana za pomocą określonego testu, np. przyjmuje się, że dana zmienna będąca przedmiotem analizy ma w populacji generalnej rozkład normalnyHipoteza alternatywna (
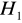
) - hipoteza statystyczna konkurencyjna względem hipotezy zerowej H0, w tym sensie, że jeżeli odrzuci się hipotezę zerową, przyjmując przy tym samym słuszność hipotezy alternatywnej, np. przyjmujemy, ze H0 powiada, ze średnia danej populacji jest równa n0, natomiast H1będzie orzekać, że wartość średnia n nie równa się wartości n0. Jeżeli będą podstawy, ażeby przyjąć H0, to H1zostaje odrzucana.
W weryfikacji hipotez statystycznych możemy popełnić określone błędy. Konieczna jest wiedza dotycząca popełnionego błędu (typu granicy itp.)
Rodzaje błędu:
Pierwszego rodzaju - jest to możliwy do popełnienia błąd przy weryfikowaniu hipotezy statystycznej, polegający na odrzuceniu hipotezy prawdziwej
Drugiego rodzaju - możliwy do popełnienia w trakcie weryfikacji statystycznej, polegający na przyjęciu hipotezy fałszywej.
Poziom istotności - bardzo małe prawdopodobieństwo popełnienia błędu pierwszego rodzaju przy testowaniu danej hipotezy.
Odrzucenie sprawdzanej hipotezy na poziomie istotności ![]()
oznacza, ze ryzyko popełnienia błędu wynosi 5% , czyli w 5 przypadkach na 100 będziemy mylili się przy procesie weryfikacji hipotez.
Test statystyczny - weryfikacja hipotezy statystycznej odbywa się poprzez zastosowanie odpowiedniego narzędzia zwanego testem statystycznym. Jest to reguła postępowania, która każdej możliwej próbie losowej przyporządkowuje decyzje przyjęcia lub odrzucenia weryfikowanej hipotezy. Wyróżniamy dwa typy hipotez statystycznych:
Prosta - to taka, która jednoznacznie określa rozkład cechy X populacji generalnej. Jeżeli np. wysuwamy hipotezę, że wartość średnia m ma określoną wartość m0 a ponadto wiemy, ze cecha X ma rozkład normalny ze znanym odchyleniem standardowym
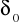
, to taka hipoteza jest hipotezą prostą, gdyż jednoznacznie specyfikuje rozkład cechy X populacji generalnej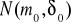
Hipoteza złożona - nie specyfikuje jednoznacznie rozkładu populacji generalnej. Np. wysuwamy hipotezę, ze wartość średnia , jest równa m0 w populacji generalnej. Zakładamy, że populacja ma rozkład normalny, nie jest jednak dana wartość odchylenia standardowego. Jest bardzo wiele takich rozkładów normalnych, które mają identyczną wartość średniej m, jednak różnią się między sobą, gdyż każdy z nich może mieć inne odchylenie standardowe.
Przykład:
Średni okres żywotności opon „Pirelli” m0 = 60 tys. km. Jeżeli zużycie opon ma rozkład normalny i znane odchylenie standardowe to taka hipoteza jest hipoteza prostą. Jeżeli jednak przy tych samych założeniach określamy hipotezę, ze zużycie opon wynosi nie mniej niż 60 tys. km,to taka hipoteza byłaby hipotezą złożoną.
Teoria weryfikacji hipotez statystycznych dostarcza podstaw, w oparciu o które są budowane reguły wnioskowania umożliwiające rozstrzygnięcie, czy w wyniku zbadania próby wysunięto hipotezę, należy ją przyjąć (tj. uznać za prawdziwą) czy też należy ją odrzucić (uznać za fałszywą).
W zależności od postaci hipotezy zerowej H0 (czyli bezpośrednio sprawdzonej) oraz w zależności od postaci H1 (czyli konkurencyjnej względem H0) sposób budowy testu jest różny. Jednak przy budowie każdego testu istota zagadnienia polega na tym, aby uchronić się przed popełnieniem błędu pierwszego rodzaju (polegającym na odrzuceniu hipotezy prawdziwej) jak i przed popełnieniem błędu drugiego rodzaju (polegającym na przyjęciu fałszywej hipotezy). Odrzucenie hipotezy w teście nie jest równoważne z logicznym określeniem jej prawdziwości czy fałszywości)
Podstawowe znaczenie w procesie weryfikacji hipotez odgrywają tzw. testy istotności. Jest to taki rodzaj testów, w którym na podstawie wyników próby losowej podejmuje się jedynie decyzje o odrzuceniu sprawdzanej hipotezy lub stwierdza się brak podstaw do jej odrzucenia. Nie podejmuje się w tym teście decyzji o przyjęciu sprawdzanej hipotezy, gdyż w tym teście bierze się jedynie pod uwagę wyłączenie błędu pierwszego rodzaju. Natomiast nie uwzględnia się w konsekwencji popełnienia błędu drugiego rodzaju.
Powstawanie testów istotności:
W zależności od postaci H0 buduje się pewna statystykę Z z wyników n-elementowej próby losowej i wyznacza się rozkład tej statystyki przy założeniu prawdziwości H0. W tym rozkładzie wybiera się taki obszar Q wartości statystyki Z, aby spełniona była następująca relacja: ![]()
. Obszar Q nazywamy obszarem krytycznym testu, gdyż ilekroć wartość statystyki Z z próby znajdzie się w tym obszarze to podejmujemy decyzje o odrzuceniu H0, na korzyść H1. W przypadku, gdy otrzymane z konkretnej próby wartość statystyki Z nie należą do obszaru krytycznego Q, to nie ma podstaw do odrzucenia hipotezy H0.
Obszar krytyczny Q został tak wyznaczony, ze przy założeniu prawdziwości H0 prawdopodobieństwo otrzymania z próby n-elementowej wartości statystyki Z należącej do tego obszaru jest znane i jest bardzo mała liczbą, a zatem takie zdarzenie nie powinno zrealizować się w przeprowadzanym doświadczeniu. Jeżeli mimo tego zrealizowało się, to musiało mieć prawdopodobieństwo większe od tego, które wynika z założenia o prawdziwości H0, wówczas jesteśmy w stanie uznać hipotezę za fałszywa i odrzucić ją. Możemy się pomylić i odrzucić hipotezę, która była prawdziwa (błąd pierwszego rodzaju), jednak prawdopodobieństwo takiej pomyłki jest bardzo małe i równe przyjętemu poziomowi istotności ![]()
.
Jeżeli wartość statystyki Z z próby n-elemntowej znalazła się poza obszarem krytycznym Q, to prawdopodobieństwo tego zdarzenia, przy prawdziwości hipotezy H0, jest równe ![]()
(to nie jest współczynnik ufności), a ta wartość jest bliska 1.
Zaszło zatem zdarzenie, które powinno zajść przy prawdziwości hipotezy, gdyż miało duże prawdopodobieństwo, a zatem nie ma podstaw do odrzucenia hipotezy H0.
Podstawą budowy obszaru krytycznego dla danego testu istotności jest rozkład odpowiedniej statystyki z próby, wyznaczony przy założeniu prawdziwości sprawdzanej hipotezy.
Decyzje i ich konsekwencje w teście sprawdzającym hipotezę H
Decyzje |
Hipoteza |
|
|
Prawdziwa |
Fałszywa |
Przyjęcie H |
Decyzja poprawna |
Decyzja błędna (błąd II rodzaju) |
Odrzucenie H |
Decyzja błędna (błąd I rodzaju) |
Decyzja poprawna |
Przykład:
Populacja generalna ma ![]()
, przy czym odchylenie standardowe ![]()
jest dane. Na podstawie wyników próby losowej n-elemntowej mamy zweryfikować ![]()
wobec ![]()
. Test istotności dla H0 jest następujący:
Na podstawie wyników próby oblicza się wartość statystyki ![]()
a następnie zmiennej losowej standaryzowanej U.
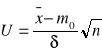
![]()
![]()
- wartość krytyczna taka, aby dla znanego z góry małego prawdopodobieństwa ![]()
zachodziła relacja:
![]()
Jeżeli ![]()
- odrzucamy hipotezę H0
Jeżeli ![]()
- nie ma podstaw do odrzucenia H0
Powyższy test jest testem z tzw. dwustronnym obszarem krytycznym, który stosujemy jedynie do takiego przypadku H1, w którym mamy ![]()
.
Jeżeli ![]()
to stosujemy test istotności z tzw. lewostronnym obszarem krytycznym, określanym nierównością ![]()
.
Wtedy wartość ![]()
wyznaczamy w taki sposób, aby zachodziła relacja: ![]()
.
Natomiast dla ![]()
stosujemy test istotności z prawostronnym obszarem krytycznym, gdzie ![]()
. Wtedy ![]()
wyznaczamy tak, aby spełniona była równość ![]()
H0 odrzucamy wówczas, gdy wyznaczona z próby wartość U będzie spełniała równość ![]()
.
Przykład
Plany żyta na powierzchniach uprawianych w pewnym województwie mają rozkład normalny N o nieznanych parametrach. Przyjmuje się, że średni plon z tych powierzchni wynosi 28 q/ha. Należy zweryfikować, czy słuszny jest pogląd, że dla 20 powierzchni otrzymano średni plon w wysokości 25 q/ha z odchyleniem ![]()
równym 4,5 q/ha. Wiemy, że ![]()
a ![]()
. Wiemy zatem, że populacja ma rozkład normalny z nieznanymi parametrami, a zatem do weryfikacji powyższej hipotezy należy zastosować znana statystykę.
![]()
- rozkład t-studenta
![]()
![]()
- poziom istotności (bardzo małe prawdopodobieństwo wystąpienia błędu pierwszego rodzaju, czyli odrzucenia hipotezy prawdziwej)
![]()
n -1 = 19 - ilość stopni swobody
Występuje obszar krytyczny dwustronny, ponieważ ![]()
.
![]()
![]()
- +wartość statystyki t z próby znalazła się w obszarze krytycznym.
Oznacza to, że hipotezę zerową orzekającą, że średni plon wynosi 28q/ha, należy odrzucić na rzecz hipotezy alternatywnej mówiącej, że średni polon żyta z ha jest różny od 28q/ha.
1
Wyszukiwarka
Podobne podstrony:
sciaga wyklad I i II, studia, rok II, EGiB, od Ani
Wykłady prof. Misala, Ekonomia, Studia, II rok, Międzynarodowe stosunki gospodarcze, Stare msg, Wykł
sciąga na II rok eko, Notatki, Stosunki miedzynarodowe, Ekonomia
wykłady dodatkowo- nowe, Ekonomia, Studia, I rok, Finanase publiczne, Wykłady-stare, Wykłady
Wykłady prof. Bednarski, Ekonomia, Studia, I rok, Finanse i bankowość, Wykłady
Rynek finansowy - ¦çw. II kolokwium, Ekonomia, Studia, II rok, Rynki finansowe
Sciagapowiekszon, SGGW - Technologia żywnosci, II semestr, SEMESTR 2, wyklady II rok, BHP ERGO, PD
podstawy ¬ywienia2, SGGW - Technologia żywnosci, II semestr, SEMESTR 2, wyklady II rok, PODSTAWY ŻY
wykłady- wszystko (Artur), Ekonomia, Studia, I rok, Finanse i bankowość, Wykłady
Obliczenia91, SGGW - Technologia żywnosci, II semestr, SEMESTR 2, wyklady II rok, od kaski
zagadnienia - wyklad 5, II ROK, III SEMESTR, Fizjologia zwierząt
Ustrój administracji rządowej i samorządowej WYKŁAD 1, II rok Administracja UKSW, Ustrój administrac
ściaga z prezentacji, II rok II semestr, BWC, egzamin przyrodo
Przedmiotem ergonomii ost, SGGW - Technologia żywnosci, II semestr, SEMESTR 2, wyklady II rok, BHP
więcej podobnych podstron