1.Najczęściej stosowane sygnały wymuszające i ich transformaty:

Skok jednostkowy

x(t)

t ≥ 0

t < 0

t

Transformata F(s) =

Sygnał liniowo narastający

x(t)

t

Transformata F(s) =

Delta Diraca (inpuls)

x(t)

t

Transformata F(s) = 1

2. Co to oznacza superpozycja obiektu.

To oznacza że obiekt wykazuje właściwości liniowe. Oznacza to, że reakcja układu liniowego na wymuszenie o postaci u=c₁u₁+c₂u₂ ma postać y=c₁y₁+c₂y₂ przy czym y₁ i y₂ stanowią wynik oddziaływania oddzielnych wymuszeń u₁ i u₂, a c₁ ic₂ są stałymi dowolnymi.

3. OPIS UKŁADÓW CIĄGŁYCH

sygnały przyjmują dowolne wartości z danego przedziału

0 - 100°C; 4 - 20mA;

Jeżeli F zależy jawnie od czasu to obiekt jest niestacjonarny. Obiekt stacjonarny jest, gdy F nie zależy od czasu.

4. Linearyzacja - Obiekt nieliniowy zastępujemy przybliżeniem liniowym wokół punktu równowagi (punkt pracy). Punkt równowagi (y₀, u₀) jest to punkt spełniający równanie ch-ki statycznej.

Δy(t) = y(t) - y₀

Δy(t) =
⋅(t)

oblicza się pochodne cząstkowe po zmiennych w punkcie pracy.

- uproszczenie modelu nieliniowego w taki sposób, że charakterystykę nieliniową przybliża się lokalnie, tzn. w pewnym obszarze, odpowiednio dobraną zależnością liniową. Jeśli nieliniowość opisuje się charakterystyką statyczną y=f(u), to w pewnym punkcie tej ch-ki np. przy u=u_o, można poprowadzić styczną do ch-ki i uznać, że w pobliżu tego punktu ch-ka pokrywa się ze styczną, a więc ma postać y=k₁u+k₀, przy czym współczynnik k₁ odpowiada nachyleniu stycznej, zaś k_o jest przesunięciem względem początku układu współrzędnych.

Linearyzacja - jest możliwa tylko lokalnie, w otoczeniu wybranego punktu u₀ i ma sens tylko dla małych odchyleń od tego punktu.

5. PRZEKSZTAŁCENIE LAPLACE'A

x(t) X(s)

orginałowi tansformatę

Własności przekształcenia Laplace'a:

• przekształcenie liniowe, które spełnia zasadę superpozycji:

a₁, b₂ - stałe; x₁, x₂ - sygnały

• 
  

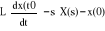
• obliczanie kolejnych pochodnych jest następujące

• całkowanie:

• opóźnienie sygnału:

6. Na czym polega rozwiązywanie równań różniczkowych za pomocą przekształceń Laplace'a

Opis za pomocą transmitancji przejścia z równania różniczkowego do równania transmitancji dokonujemy obustronnego przekształcenia Laplace'a przy zerowych warunkach początkowych:

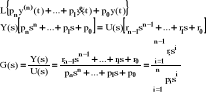
7. inna ściąga

8 rysunki ręczne.

9. Stan obiektu opisujemy za pomocą n - zmiennych X₁, X₂ ,X_3, ...X_n.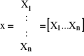

Interpretacja fizyczna - „zbiorniczka” energii;

Interpretacja matematyczna - kolejne pochodne sygnału wyjściowego y(t).

10. Charakterystyki skokowa i impulsowa w zależności od położenia biegunów na płaszczyźnie zespolonej

Płaszczyzna Gausa

I_m

czł. oscylacyjny czł. inercyjny czł. oscylacyjny bez tłumienia

dwa pierwiastki na I_m

R_e

czł. całkujący

pierwiastek = 0

11.Własności ch-ki skokowej członu inercyjnego I-go rzędu.

gdzie: k - współczynnik wzmocnienia

T - stała czasowa

Równanie różniczkowe:

Charakterystyka skokowa ma postać:

y(t)

k

T₁

T₂

T₃

t

T₃ > T₂ > T₁

k - określa wartość sygnału wyjściowego w stanie równowagi

Graficzna definicja (postać) stałej czasowej

y(t) styczna w punkcie ‚0'

k

t

t	Y(t)
T	63 %
3T	95 %
5T	99 %

12. Jak opisuje się oddziaływanie zakłócenia na obiekt.

Należy tak zwiększyć (zmienić) sygnał u = u₀ + Δu, tak żeby na wyjściu ponownie otrzymać y₀ w stanie ustalonym.

Δy - zmiana sygnału wyjściowego spowodowana zmianą sygnału sterującego;

13. Klasyfikacja obiektów termo-energetycznych z punktu widzenia automatyki

Obiekty, w których następuje wymiana ciepła, przepływ płynów.

1. Obiekty z wyrównaniem (statyczne).

2. Obiekty bez wyrównania (astatyczne).

Charakterystyki skokowe obiektów z wyrównaniem

inercyjne i opóźniające

y(t)

T

Charakterystyki skokowe obiektów bez wyrównania

y(t)

Metoda doświadczalna wyznaczania modeli zastępczych obiektów

z

y

u

Wyznaczamy własności obiektu w torze sterowania podając na wejście skok jednostkowy u(t) i rejestrując wyjście.

Klasyfikujemy obiekty do jednej z klas.

Obiekty z wyrównaniem

y(t) y_∞ obiekt rzeczywisty

model Kirpfmillera

y₀

t

T₀

Modele obiektów z wyrównaniem

1. Model Kirpfmillera

T_z - zastępcza stała czasowa opóźnienia; k - współczynnik wzmocnienia; T₀ - zastępcze opóźnienie;

2. Model Strejca:

n - rząd inercyjności; T - stała czasowa inercyjności;

T_t - opóźnienie transportowe;

3. Model Rotacza:

inercja I-go rzędu i-człon opóźniający

14 Sposoby wyznaczania własności dynamicznych:

1) Metoda doświadczalna - wykonywanie eksperymentu polegającego na pobudzaniu obiektu określonym sygnałem sterującym (np. skok jednostkowy) i zarejestrowaniu odpowiedzi;

2) Metoda analityczna - polega na wyprowadzeniu równań łączących wielkości wejściowe i wyjściowe (bilans energii lub substancji);

15 Regulatory (ciągłe)

y(t)

u(t) + w_z

UAR - układ automatycznej regulacji

1. Regulator proporcjonalny /typ P/

2. Regulator proporcjonalno-całkujący /typ PI/

3. Regulator proporcjonalno-różniczkujący /typ PD/

4. Regulator proporcjonalno-całkująco-różniczkujący /typ PID/

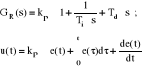
k_p, T_i, T_d - nastawy regulatora T_i - czas zdwojenia

T_d - czas wyprzedzenia

Typ P

u(t) u(t)

k_p

1

t t

Typ PI

u(t)

ΔU

k_p

ΔU

t

T_i T_i

Typ PD

u(t) u(t)

t δ(t) t

20 (21). Kryteria Stabilności

W kryterium Nyquista bada się wyrażenie:

G₀(s)⋅G_r(s)+1=0 G₀(s)⋅G_r(s) = -1

Iloczyn
jest połączeniem szeregowym obiektu i regulatora.

układ regulacji w stanie otwartym

Jeżeli układ regulacji w stanie otwartym jest stabilny, to kryterium Nygnista brzmi następująco:

Jeżeli charakterystyka amplitudowo-fazowa układu otwartego nie obejmuje punktu (-1,0) to układ w stanie zamkniętym jest stabilny.

Charakterystyka amplitudowo-fazowa układu otwartego

Im

Do pytania20

stabilny

Re

na granicy stabilności

niestabilny

Im

na granicy stabilności

Re

stabilny

uzupełnienie

niestabilny

1. Należy wyznaczyć charakterystykę amplitudowo-fazową. Można to zrobić doświadczalnie pobudzając układ otwarty sygnałami sinusoidalnymi o różnej częstotliwości.

2. stwierdzamy czy charakterystyka obejmuje punkt (-1,0)

Kryterium Hurwitza

Wielomian
jest stabilny asymptotycznie wtedy i tylko wtedy, gdy spełnione są dwa warunki:

1. wszystkie współczynniki są dodatnie p₁ > 0; i = 0,1,...,n;

2) wyznacznik główny Δ_n i podwyznacznik Δ_n+1,...., Δ₁ są dodatnie

22. Cele syntezy układu regulacji automatycznej.

- zapewnić stabilność

- wyeliminować odchyłkę statyczną

- spełnić wymogi co do kształtu przebiegu przejściowego

23. Jak eliminuje się odchyłkę statyczną?

Poprzez stosowanie w regulatorze części całkującej. Ceną jaką płaci się za eliminacją e_s są oscylacje.

24. Idealny przebieg przejściowy.

y(t)

dla idealnego przebiegu

e_s = e_d = Κ =t_r = 0

t

25. Dobór nastaw regulatorów

1 - analityczna

2 - doświadczalna

ANALITYCZNA - należy znać model obiektu w postaci:

Nastawy wylicza się z podanych zależności, tak aby osiągnąć minimum jednego z kryteriów całkowych.

Kryteria całkowe: do pytania 19

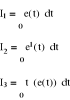
e(t)

t

METODA ZIEGLERA-NICHOLASA

• Nie trzeba znać modelu obiektu

• 
  Należy wykonać eksperyment (do obiektu dołącza się regulator P i nastawia się T_d = 0 T_i = ∞)

• Zwiększa się wzmocnienie k_p, aż przebieg przejściowy będzie oscylacyjny bez tłumienia

e(t)

T_kr

T

• Wylicza się k_p, T, T_d w zależności od k_pkr, T_kr

26. Jak zachowuje się obiekt liniowy pobudzony sygnałem

sinusoidalnym.

Jeżeli na wejście obiektu liniowego wprowadzi się sygnał sinusoidalny to po dostatecznie długim czasie na wyjściu ustalają się drgania w postaci sygnału sinusoidalnego o tej samej częstotliwości, lecz o innej amplitudzie, fazie.

u(t)

u(t) y(t)

28. Układy sterowania logicznego - podział:

Układy, w których wszystkie sygnały mogą przyjmować tylko dwie wartości „0” i „1” nazywamy układami logicznymi.

• Układy kombinacyjne - wartości na wyjściu zależą tylko od bieżących stanów na wyjściu;

• Układy sekwencyjne (z pamięcią) - wartości na wyjściu zależą od bieżących stanów na wejściu oraz od poprzedniego stanu układu;

• Układy synchroniczne - w których zmiany sygnałów mogą występować tylko w określonych chwilach czasu (z zegarem);

• Układy asynchroniczne - w których zmiana sygnałów może nastąpić w dowolnym momencie;

29. Sposoby realizacji funkcji logicznych:

SCHEMATY DROBINKOWE

+ -

część część

warunkowa wykonawcza

W części warunkowej umieszcza się elementy, które powodują załączanie urządzenia znajdującego się w części wykonawczej.

Zestyk zwierny

Zestyk rozwierny

Przycisk niestabilny

Przycisk stabilny

30. Postacie kanoniczne funkcji logicznych:

postać alternatywna:

postać koniunkcyjna

postać kanoniczna dla funkcji równoważności

x1 x2 x1≡x2

0 0 1 =f(0,0)

0 1 0 =f(0,1)

1 0 0 =f(1,0)

1 1 1 =f(1,1)

x1≡x2=f(x1,x2)=

31. Prawa algebry Boole'a - Metody dowodzenia

prawa powtórzenia x + x = x x ⋅ x = x

działania na elementach 0,1

x ⋅ 0 = 0 x + 0 = x

x ⋅ 1 = x x + 1 = 1

reguły pochłaniania

1) x₁+x₁⋅x₂ = x₁

2) x₁ + (
⋅x₂) = x₁ + x₂

Dowód 1)

L=x₁+x₁⋅x₂ = x₁⋅1+x₁⋅x₂ =x₁⋅(x₂+1)=x₁⋅1=x₁=P

Reguły sklejania

(x₁+x₂)(x₁+
)=x₁

x₁ ⋅ x₂ + x₁ ⋅
= x₁

32. Metody minimalizacji

Minimalizacja funkcji logarytmicznych metodą KARNAUGHTA

Metoda opiera się na prawach sklejania

• Tworzenie tabeli K... - dwie kolejne rubryki mogą różnić się wartością tyko jednej zmiennej;

• Należy sklejać „0” lub „1” wybrać tę wartość, która występuje mniej razy;

• Każdą kratkę zawierającą sklejaną wartość należy uwzględnić co najmniej raz;

• Można sklejać 2, 4, 8, 16 klatek;

• ]sklejanie kratki obwodzi się linią, apisuje się w odpowiedniej postaci kanonicznej w składniku występują tylko te zmienne, które nie zmieniają wartości w sklejanych kratkach;

• zasady negowania są takie jak w zwykłej postaci kanonicznej;

34. Schemat rzeczywistego układu regulacji

z(s)

u(s) Y(s)

układ

układ wykonawczy pomiarowy

E(s) - Y_m(s)

Y_z(s)

stacyjka operatorska

E(s)=Y_z(s) - Y_m(s)

35. Podział regulatorów ze względu na rodzaj energii pomocniczej:

-pneumatyczne (wzmacniacz, dysza, przysłona)

- hydrauliczne (wzmacniacz z rurką strumieniową)

- elektryczne (elektroniczne)

- bezpośredniego działania (bez energii pomocniczej)

40. Kaskadowy układ regulacji

z₁ z₂

U Y

41. Kombinowany układ regulacji (zamknięto-otwarty)

z

y

u

y

y_z

-

42. Człon sprzęgający G_s(s) można tak zaprojektować, aby transmitancja w torze zakłócenie z - wielkość wyjściowa y była równa 0.

układ kaskadowy

Rozważmy sytuację:

inercja 1-go rzędu

regulator proporcjonalny

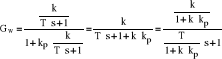
Dla dużego współczynnika wzmocnienia k_p :

Regulator pomocniczy G_R2(s) - jest regulatorem proporcjonalnym, jego nastawy dobiera się dla obiektu G₁(s).

Regulator główny G_R1(s) dobiera się do obiektu będącego połączeniem G₂(s) i G_w(s).

G_z(s)

G₀(s)

Regulator

Obiekt

G₀(s)

G_R(s)

χ - 40%

e_d - duża; t_r- mały

χ - 20%

e_d, t_r - wartości średnie

k_pkr - współczynnik wzmocnienia przy którym

wystąpiły drgania nietłumione

G_z(s)

G_o(s)

Nastawnik

(zawór)

siłownik

Regulator

Czujnik

Przetwornik

Zadajnik

G₁(s)

G_R2(s)

G₂(s)

G_R1(s)

G₁(s)

G_R2(s)

G₂(s)

G_R2(s)

G_R1(s)

G₂(s)

G_o(s)

G_R(s)

G_s(s)

---