Całkując równanie dW=-gdh w przedziale Wo, Wp otrzymujemy 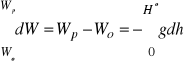
Wprowadzając średnią wartość gśr przyśpieszenia g na wysokość Ho mamy Wp-Wo = - gśrHo, skąd ostatecznie
1. Odchylenie pionu - podac składowe, rysunek i opis do czego sluzy odchylenie i anomalia grawimetryczna bo to sie z tym wiaze
2. bylo cos o wysokosciach normalnych i chyba ortometrycznych
3. bylo o potencjale
Omów istotę wyznaczenia wysokości ortometrycznej i normalnej.
Wyjaśnij pojęcia: linia pionu, geoida, anomalie pola ciężkości.
Geoida i quasigeoida - definicje i ich związek z systemem wysokości.
Porównać system wysokości ortometrycznych i normalnych. PATRZ PYT.11 - BYŁO Dlaczego idąc ciągiem niwelacji precyzyjnej o długości 80 km, należy wprowadzać poprawki.
Omówić istotne różnice systemu wysokości. Definicja odchylenia od pionu, w czym jest wykorzystywana.
Podaj definicję: Geoida, quasigeoida, anomalie pola ciężkości, linia pionu, wysokość ortometryczna i normalna i sposoby ich wyznaczania.
Do czego jest potrzebna znajomość odchylenia linii pionu oraz odstępu od geoidy.
Podać systemy wysokości ortometrycznych i normalnych. Jest dany ciąg niwelacyjny o długości 80 km na kierunek północ - południe. Oblicz wszystkie znane ci poprawki występujące w geodezji wyższej.
Definicja geoidy i quasigeoidy oraz ich związek z poszczególnymi systemami wysokości. Odchylenie linii od pionu i jej znaczenie w geodezji.
Zewnętrzne pole grawitacyjne Ziemi, właściwości powierzchni ekwipotencjalnych.
Odchylenie pionu i jego znaczenie w pracach inżynierskich
Systemy wysokości
Omów system wysokości obowiązujący w Polsce i podaj zalety jego stosowania. Podaj ogólne zasady wyznaczania modelu Ziemi na danym obszarze np. w Polsce.
Wyjaśnij pojęcia: zewnętrzne i normalne pole grawitacyjne Ziemi, odchylenie pionu
Różnice między wysokością ortometryczną a normalną. Dlaczego przy ciągu niwelacji precyzyjnej I klasy o dł. 80 km stosujemy poprawkę normalną lub ortometryczną.
Opisać systemy wysokości.
Poprawki uwzględniane przy niwelacji precyzyjnej.
Wyjaśnij pojęcia : zewnętrzne i normalne pole grawitacyjne Ziemi; odchylenie pionu
Omów istotę wyznaczenia wysokości ortometrycznej i normalnej.
Przez wysokość ortonormalną rozumiemy odległość tego punktu od geoidy, jako powierzchni morza, mierzoną wzdłuż linii siły ciężkości.
Całkując równanie dW=-gdh w przedziale Wo, Wp otrzymujemy 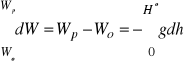
Wprowadzając średnią wartość gśr przyśpieszenia g na wysokość Ho mamy Wp-Wo = - gśrHo, skąd ostatecznie
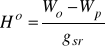
Przez wysokość normalną rozumiemy odległość liczoną wzdłuż linii pionowej od quasigeoidy do danego punktu.
Do wyznaczenia wysokości normalnej wykorzystuje się metodę niwelacji astronomicznej lub praktycznie, metodę niwelacji astronomiczno-grawimetrycznej.
Systemy wysokości
Wysokość ortometryczna - odmierzona jest od powierzchni Ziemi do geoidy wzdłuż linii siły ciężkości, prostopadła w każdym punkcie do powierzchni ekwipotencjalnej.
Określamy przeciętną wartość przeciętnego przyspieszenia g (wzdłuż linii pionu od geoidy do pkt P). Wysokość ortometryczna jest równa długości odcinka linii pionu (krzywej)
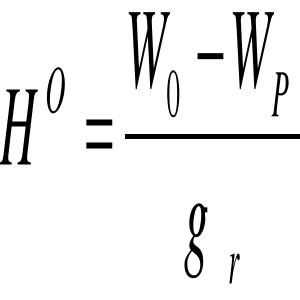
Wys normalna -wysokość punktu P wzdłuż normalnej do elipsoidy jest to system wysokości uwolniony od hipotez dotyczących rozkładu mas HNOR=C\ၧ-przeciętna wartość przyspieszenia normalnego wzdłuż linii pionu pola normalnej siły ciężkości. Jest to odległość telluroidy od elipsoidy.
![]()
Wys dynamiczna - cecha charakteryzuje punkty wybranej powierzchni ekwipotencjalnej które mają te same wysokości dynamiczne, czyli nie uwzględniają nierównoległości powierzchni ekwipotencjalnych.
Mają istotne znaczenie np. dla projektów wodnych na dużych obszarach, gdy wymagana jest duża dokładność projektowania spadków.
![]()
Wyjaśnij pojęcia: linia pionu, geoida, anomalie pola ciężkości.
Linia pionu - normalna do geoidy; wyznaczana przez kierunek siły ciężkości; to krzywa o takich własnościach, że proste styczne w każdym punkcie mają kierunek wektora przyspieszenia siły ciężkości![]()
, czyli wektor wypadkowej siły przyciągania i odśrodkowej w danym punkcie. Linie pionowe są styczne do powierzchni ekwipotencjalnych. Linie sił ciężkości, czyli linie pionu są na ogół liniami krzywymi, płaskimi, zwróconymi wypukłością w stronę równika
UZUPEŁNIENIE
Kierunek siły ciężkości nie pokrywa się z kierunkiem normalnej do elipsoidy odniesienia. Różnica ta nazywa się odchyleniem pionu. Ponieważ prowadzenie wszelkich prac obliczeniowych geodezji wyższej jest możliwe tylko na matematycznej powierzchni elipsoidy, więc znajomo odchyleń pionu jest niezbędna do redukcji na powierzchnię odniesienia tych wszystkich pomiarów kątowych, które wykonano wg siły ciężkości.
Znajomość odchyleń pionu na dostatecznie dużym obszarze pozwoli określić nie tylko poszukiwany kształt geoidy, przecinającej kierunki pionów zawsze pod kątem prostym, ale pozwoli także określić położenie geoidy względem elipsoidy odniesienia, czyli znaleźć odstępy między powierzchnią geoidy i elipsoidy. Dane te są niezbędne do redukcji baz triangulacyjnych na elipsoidę: musimy najpierw uwzględnić wysokość bazy npm, czyli nad geoidą, a następnie odstęp geoidy od elipsoidy odniesienia, który może wynieść kilkadziesiąt metrów. W miejscach pomiaru baz trzeba go wyznaczyć z dokładnością nie mniejszą niż 3m.
Odchylenia pionów można wyznaczyć nie tylko na podstawie pomiarów grawimetrycznych, lecz również na podstawie pomiarów astronomicznych, wykonanych na punktach triangulacyjnych. Pomiary te wykonujemy zgodnie z kierunkiem pionu, który po przedłużeniu go w kierunku przeciwnym do kierunku siły ciężkości wyznaczy na kuli niebieskiej tzw. zenit astronomiczny, różny od zenitu geodezyjnego, wyznaczonego przez normalną do elipsoidy. Ze względu na niepokrywanie się tych dwóch punktów zenitalnych zachodzi potrzeba rozróżniania współrzędnych astronomicznych od geodezyjnych.
Położenie zenitu geodezyjnego względem zenitu astronomicznego, czyli względem pionu miejsca obserwacji, wyznacza się przez dwie wielkości kątowe: ξ i η, wyrażane w sekundach łuku. Są to prostokątne współrzędne sferyczne zenitu geodezyjnego w układzie dwu wzajemnie prostopadłych kół wielkich jako osi współrzędnych, a mianowicie: południka astronomicznego i pierwszego wertykału miejsca obserwacji. Łuki tych kół wielkich przecinają się w zenicie astronomicznym, który jest początkiem przyjętego układu współrzędnych. Wielkości ξ i η oznaczają więc odpowiednio na kuli niebieskiej odległości kątowe zenitu geodezyjnego od pierwszego wertykału i od południka miejscowego. Są to składowe odchylenia pionu w danym miejscu i na ogół ich wartość nie przekracza kilkunastu sekund.
Różnice obliczonych współrzędnych geodezyjnych B i L oraz pomierzonych astronomicznych φ i λ pozwolą wyznaczyć składowe ξ i η odchylenia pionu w badanym punkcie z zależności:
ξ = φ - B
η = (λ - L)cos φ.
Znając ξ i η dla danego punktu triangulacyjnego, możemy na nim wykonać redukcję wszystkich pomiarów kątowych na elipsoidę.
Azymut astronomiczny, liczony od południka astronomicznego, zredukujemy na elipsoidę równaniem Laplace'a: Ag=A - η tg φ.
Geoida - powierzchnia ekwipotencjalna (o stałym potencjale) zawierająca średni poziom mórz i oceanów. Nie jest opisywalna matematycznie, nie przedstawiają jej funkcje analityczne (opisywalna tylko punktowo). Inaczej jest to idealny swobodny poziom mórz otwartych o jednakowym potencjale [za naturalną powierzchnię ekwipotencjalną można uważać lustro połączonych wód mórz i oceanów w stanie spoczynku, przedłużone pod lądami i nad depresjami. Tak pomyślana powierzchnia jest ciągła i zamknięta, lecz nie da jej się wyrazić równaniem matematycznym - jest nieregularna. Różny bowiem stopień zasolenia wody, a więc różna jej gęstość sprawia, iż wektory siły ciężkości w różnych punktach takiej powierzchni odchylają się od normalnej względem elipsoidy ziemskiej, zawsze w stronę mas o większej gęstości. Podobnie dzieje się na obszarze lądowym - wskutek niejednorodnej budowy skorupy ziemi. W miejscach odchylenia wektorów siły ciężkości, a tym samym linii pionu od normalnej względem elipsoidy, również geoida - jako zerowa powierzchnia ekwipotencjalna - odchyla się od powierzchni elipsoidy. Geoidę przyjmujemy za rzeczywisty kształt ziemi. Opisuje ją równanie: W=W0=const, gdzie W - potencjał siły ciężkości (potencjał ciężkościowy).
Anomalie pola ciężkości - wyraża je wzór Δg = g' - γ, gdzie: g' - wartość pomierzonego przyspieszenia g z uwzględnieniem redukcji Faye'a i in., γ - wartość normalna przyspieszenia wg wzoru Helmerta; anomalie siły ciężkości są nieuniknionym następstwem różnej gęstości mas i nieregularnego ich rozmieszczenia w bryle ziemskiej; wartość ujemna anomalii w danym punkcie świadczy o tym, że w otoczeniu tego punktu gęstość mas jest mniejsza od przeciętnej, natomiast anomalie dodatnie wskazują na istnienie w tym otoczeniu mas o większej gęstości.
[Można udowodnić, że w danym punkcie pierwsza pochodna potencjału W jest równa przyspieszeniu g siły ciężkości w tym punkcie. W i g odnoszą się do nieregularnej powierzchni geoidy i mogą być wyznaczane tylko doświadczalnie pomiarami grawimetrycznymi. Natomiast potencjał normalny U i jego pierwsza pochodna γ, czyli przyspieszenie normalne, odnoszą się do sferoidy normalnej, a więc powierzchni wyrażanej analitycznie. Z tego wynika, że przyspieszenie γ i odpowiadający mu potencjał U w dowolnym punkcie na sferoidzie normalnej można obliczyć, jeżeli tylko znane są parametry sferoidy i położenie punktu. Jest to b. trudne, ale wzór został opracowany przez Helmerta:
γ = 978030(1+0,005302 sin2φ - 0,000007 sin22φ)
Wartości normalne γ przyspieszenia i wartości przyspieszenia g z pomiarów grawimetrycznych nie są porównywalne, gdyż punkt P fizycznej powierzchni ziemi nie leży w ogólnym przypadku na powierzchni odniesienia, lecz nad nią lub pod nią w odległości H. Natomiast przyspieszenie normalne γ, odpowiadające szerokości geograficznej punktu P odnosi się do rzutu P' na poziom zerowy (powierzchnię odniesienia). Trzeba tu wziąć pod uwagę, że na odcinku H linii pionu lub na normalnej pomiędzy poziomami P i P' wartość przyspieszenia zmienia się, gdyż jest zależna od odległości punktu P od środka mas ziemi. Zachodzi konieczność doprowadzenia do porównywalności przyspieszenia pomierzonego g z przyspieszeniem normalnym γ. Uzyskujemy tę porównywalność przez wprowadzenie redukcji do pomierzonej wartości g, sprowadzając ją do g' przez stosowanie odpowiednich redukcji tak, aby była ona taka jak uzyskana gdyby pomiar wykonywany był w P' na poziomie zerowym. W tym celu wprowadzamy ze względu na różnicę wysokości między punktami P i P' redukcję Faye'a oraz ze względu na wpływ masy zawartej między powierzchnią odniesienia a powierzchnią ziemi - redukcję Bourguera. Dopiero po ich wprowadzeniu normalna wartość przyspieszenia γ i zredukowana wartość przyspieszenia g' staną się porównywalne, lecz nie muszą być wzajemnie równe. Różnica między nimi to właśnie anomalia siły ciężkości.]
Geoida i quasigeoida - definicje i ich związek z systemem wysokości.
Geoida - Powierzchnia ekwipotencjalna, która zawiera w sobie swobodną powierzchnię oceanów. Geoida jako zerowa powierzchnia ekwipotencjalna przedstawia prawdziwy kształt (figurę) Ziemi.
Quasigeoida - nie jest powierzchnią ekwipotencjalną, lecz można ją jednoznacznie wyznaczyć. Na obszarze oceanów quasigeoida pokrywa się z geoidą, a pod lądami odstępy tych powierzchni nie przekraczają 2m.
Związki z poszczególnymi systemami wysokości:
wysokość ortometryczna = wysokość tego punktu ponad geoidą, liczoną wzdłuż linii siły ciężkości przechodzącej przez punkt P..
wysokość normalna = liczymy wzdłuż linii pionowej od quasigeoidy do danego punktu
wysokość dynamiczna=
Geoida - powierzchnia ekwipotencjalna (o stałym potencjale) zawierająca średni poziom mórz i oceanów. Nie jest opisywalna matematycznie, nie przedstawiają jej funkcje analityczne (opisywalna tylko punktowo). Inaczej jest to idealny swobodny poziom mórz otwartych o jednakowym potencjale [za naturalną powierzchnię ekwipotencjalną można uważać lustro połączonych wód mórz i oceanów w stanie spoczynku, przedłużone pod lądami i nad depresjami. Tak pomyślana powierzchnia jest ciągła i zamknięta, lecz nie da jej się wyrazić równaniem matematycznym - jest nieregularna. Różny bowiem stopień zasolenia wody, a więc różna jej gęstość sprawia, iż wektory siły ciężkości w różnych punktach takiej powierzchni odchylają się od normalnej względem elipsoidy ziemskiej, zawsze w stronę mas o większej gęstości. Podobnie dzieje się na obszarze lądowym - wskutek niejednorodnej budowy skorupy ziemi. W miejscach odchylenia wektorów siły ciężkości, a tym samym linii pionu od normalnej względem elipsoidy, również geoida - jako zerowa powierzchnia ekwipotencjalna - odchyla się od powierzchni elipsoidy. Geoidę przyjmujemy za rzeczywisty kształt ziemi. Opisuje ją równanie: W=W0=const, gdzie W - potencjał siły ciężkości (potencjał ciężkościowy).
W stosunku do geoidy liczona jest wysokość ortometryczna: określa ona wzniesienie punktu ponad geoidę mierzone po rzeczywistej linii pionu. Obliczamy ją przez podzielenie liczby geopotencjalnej przez przeciętną wartość przyspieszenia siły ciężkości wzdłuż linii pionu od geoidy do punktu na fizycznej powierzchni ziemi:
![]()
Przeciętną wartość przyspieszenia obliczamy ze wzoru:
![]()
Jest to przeciętna wartość rzeczywistego przyspieszenia siły ciężkości dla punktu A. wysokości ortometryczne nie mogą być dokładnie wyznaczone, gdyż pomierzone wartości średniego przyspieszenia na odcinku linii pionu praktycznie nie jest wykonalne.
Quasigeoida jest powierzchnią bardzo nieznacznie różniącą się od geoidy - pokrywa się z geoidą na powierzchni oceanów oraz z tymi punktami na lądzie, dla których średnia wartość przyspieszenia normalnego γ jest równa średnie wartości przyspieszenia faktycznego siły ciężkości g. Dla terenów równinnych rozbieżność między obu powierzchniami wynosi zaledwie parę cm, a dla terenów górzystych sięga ok. 1 m.
W stosunku do quasielipsoidy liczona jest wysokość normalna. W tym systemie rzędne zniwelowanych punktów fizycznej powierzchni ziemi zostają określone jednoznacznie - punkty leżące na jednej powierzchni ekwipotencjalnej i na jednej szerokości geograficznej otrzymują wysokości jednakowe.
Wysokość normalna określa wzniesienie punktu ponad quasigeoidę mierzone po normalnej linii pionu. Obliczamy ją przez podzielenie liczby geopotencjalnej przez przeciętną wartość normalnego przyspieszenia siły ciężkości wzdłuż normalnej linii pionu od quasigeoidy do punktu na fizycznej powierzchni ziemi:
![]()
Wartość γP oblicza się łatwo dla szerokości określanego punktu, a następnie redukuje do odpowiedniego poziomu ekwipotencjalnego odpowiadającego średniemu przyspieszeniu normalnemu:
![]()
Porównać system wysokości ortometrycznych i normalnych. PATRZ PYT.11 - BYŁO Dlaczego idąc ciągiem niwelacji precyzyjnej o długości 80 km, należy wprowadzać poprawki.
Przez wysokość ortonormalną rozumiemy odległość tego punktu od geoidy, jako powierzchni morza, mierzoną wzdłuż linii siły ciężkości.
Przez wysokość normalną rozumiemy odległość liczoną wzdłuż linii pionowej od qasigeidy do danego punktu.
W Polsce obowiązuje system wysokości normalnych odniesiony do poziomu morza w Kronsztadzie.
Metody niwelacji geometrycznej słuszne dla niewielkich obszarów, zastosowane do dużych obszarów, wymagających uwzględnienia elipsoidalnego przybliżenia kształtu ziemi, prowadziłyby do błędnych wyników. Metoda „ze środka” eliminowałaby tylko część błędu spowodowanego krzywizną ziemi, ponieważ krzywizna ta nie jest stała jak na kuli, lecz zmienna.
Błędy niwelacji ze środka osiągnęłyby maksimum przy południkowym kierunku ciągu niwelacyjnego (wzdłuż elipsy południkowej), a byłyby najmniejsze w ciągach równoleżnikowych. Błąd ten ma charakter błędu systematycznego i jako taki narasta w miarę wydłużenia ciągu, a od pewnego momentu przekracza wartość błędu dopuszczalnego dla danej kategorii pomiarów wysokościowych.
Przyjmijmy dwa punkty A i B na fizycznej powierzchni ziemi, i że przyspieszenia siły ciężkości gA i gB nie są jednakowe ze względu na różne szerokości geograficzne punktów i różne ich wzniesienie nad poziomem morza. Punkty A i B leżą więc na różnych powierzchniach ekwipotencjalnych współśrodkowych i współosiowych z elipsoidą odniesienia.
Przesuniecie punktu materialnego na dowolnej powierzchni ekwipotencjalnej nie wymaga zgodnie z zasadami mechaniki żadnej pracy (o ile pominiemy tarcie).
Wynika z tego, że trasa AA'B wymaga pracy: gAAA'=gAh1.
Trasa AB'B wymaga pracy: gBBB'=gBh2.
Z praw mechaniki wynika, że wartość pracy nie zależy od drogi, więc: gAh1= gBh2.
Ale przyspieszenia siły ciężkości w A i B nie są równe, dlatego: h1≠h2.
Z powyższego wynika, że powierzchnie ekwipotencjalne przechodzące przez punkty na różnych wysokościach terenu nie są wzajemnie równoległe w sensie geometrycznym. Stąd wniosek, że wysokości punktów leżących na jednym poziomie ekwipotencjalnym odniesionym do średniego poziomu morza jako zerowej powierzchni ekwipotencjalnej, nie są równe.
Wynika z tego, że różnica wysokości punktów to iloraz różnicy potencjałów w tych punktach i średniego przyspieszenia na długości ciągu niwelacyjnego od A do B:
![]()
Poprawki są niezbędne, aby wysokości obliczane w różnych systemach były porównywalne. Dlatego wprowadza się poprawkę dynamiczną, orotmetryczną, normalną.
Uwzględnić trzeba też poprawki „wyrównujące” rozkład mas w ziemi. Są to poprawki: Faye'a (wolnopowietrzna - nie uwzględniamy mas zalegających między A i A'), Bourguera (uwzględniająca masy - stosowana w geologii poszukiwawczej), poprawkę topograficzną (terenową - wartość g zależy do mas zalegających pod i nad punktem A - zrównanie).
Na odcinku h linii pionu lub na normalnej pomiędzy poziomami A i A' wartość przyspieszenia zmienia się, gdyż jest zależna od odległości punktu A od środka mas ziemi. Zachodzi konieczność doprowadzenia do porównywalności przyspieszenia pomierzonego g z przyspieszeniem normalnym γ. Uzyskujemy tę porównywalność przez wprowadzenie redukcji do pomierzonej wartości g, sprowadzając ją do g' przez stosowanie odpowiednich redukcji tak, aby była ona taka jak uzyskana gdyby pomiar wykonywany był w A' na poziomie zerowym. W tym celu wprowadzamy ze względu na różnicę wysokości między punktami A i A' redukcję Faye'a oraz ze względu na wpływ masy zawartej między powierzchnią odniesienia a powierzchnią ziemi - redukcję Bourguera. Dopiero po ich wprowadzeniu normalna wartość przyspieszenia γ i zredukowana wartość przyspieszenia g' staną się porównywalne, lecz nie muszą być wzajemnie równe. Różnica między nimi to anomalia siły ciężkości.
Omówić istotne różnice systemu wysokości. Definicja odchylenia od pionu, w czym jest wykorzystywana.
Podaj definicję: Geoida, quasigeoida, anomalie pola ciężkości, linia pionu, wysokość ortometryczna i normalna i sposoby ich wyznaczania.
Geoida - Powierzchnia ekwipotencjalna, która zawiera w sobie swobodną powierzchnię oceanów. Geoida jako zerowa powierzchnia ekwipotencjalna przedstawia prawdziwy kształt (figurę) Ziemi.
Quasigeoida - teoretyczna powierzchnia aproksymująca swobodny poziom mórz i oceanów w systemie wysokości normalnych.
Odchylenie linii od pionu= kąt między wektorami przyśpieszenia rzeczywistego i normalnego.
Rzut wektora na płaszczyznę I wertykału i południa astronomicznego wyznaczają składowe odchylenia pionu: wschodnią i północną. Inaczej , nazywamy składową odchylenia pionu w I wertykale, a składową południkową. Odchylenie pionu w dowolnym punkcie P zewnętrznego pola grawitacyjnego będzie zależało od przyjętej elipsoidy Uo = const potencjału normalnego U. Znaczy to, że linie siły ciężkości grawitacyjnych pól normalnych wytworzonych przez elipsoidę ziemską i elipsoidę odniesienia, które mają różne wielkości (a,α) i orientacje e bryle Ziemi, będą miały różne kierunki w punkcie P. Ponieważ wektor g jest jeden (praktycznie niezmienny) w punkcie P, więc odchylenie pionu między wektorem g a wektorami γ' - normalnego pola grawitacyjnego elipsoidy ziemskiej i γ - normalnego pola grawitacyjnego elipsoidy odniesienia będą różne.
Przez odchylenie linii pionu rozumiemy również kąt θ między prostą styczną do linii pionu w punkcie P a normalną do elipsoidy odniesienia. Ponieważ normalna do elipsoidy i styczna do linii siły ciężkości pola normalnego leżą w płaszczyźnie I wertykału wyraża się wzorem analogicznym jak składowa odchylenia pionu ϑ: η= (λ-L)cosB , a składowa ξ' odchylenia pionu θ w płaszczyźnir południka wyraża się wzorem:
ξ'=ϕ - B= ξ + 0,171”H sin 2B
gdzie H jest wyrażone w km.
Przez wysokość ortonormalną rozumiemy odległość tego punktu od geoidy, jako powierzchni morza, mierzoną wzdłuż linii siły ciężkości.
Całkując równanie dW=-gdh w przedziale Wo, Wp otrzymujemy 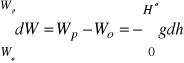
Wprowadzając średnią wartość gśr przyśpieszenia g na wysokość Ho mamy Wp-Wo = - gśrHo, skąd ostatecznie
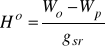
Przez wysokość normalną rozumiemy odległość liczoną wzdłuż linii pionowej od qasigeidy do danego punktu.
Do wyznaczenia wysokości normalnej wykorzystuje się metodę niwelacji astronomicznej lub praktycznie, metodę niwelacji astronomiczno-grawimetrycznej.
Do czego jest potrzebna znajomość odchylenia linii pionu oraz odstępu od geoidy.
Podać systemy wysokości ortometrycznych i normalnych. Jest dany ciąg niwelacyjny o długości 80 km na kierunek północ - południe. Oblicz wszystkie znane ci poprawki występujące w geodezji wyższej.
Przez wysokość ortonormalną rozumiemy odległość tego punktu od geoidy, jako powierzchni morza, mierzoną wzdłuż linii siły ciężkości.
Przez wysokość normalną rozumiemy odległość liczoną wzdłuż linii pionowej od qasigeidy do danego punktu.
W Polsce obowiązuje system wysokości normalnych odniesiony do poziomu morza w Kronsztadzie.
Rodzaje poprawek:
Poprawka komparacji łat: (średnia z wyników badań przed i po sezonie pomiarowym)
Poprawka termiczna, uwzględniająca średnie temperatury powietrza i taśm łat oraz współczynnik rozszerzalności taśm łat.
Poprawka lunisolarna, uwzględniająca dobowe zmiany kierunku linii pionu spowodowane przez księżyc i słońce
Poprawka normalna, ze względu na nierównoległość powierzchni poziomych (ekwipotencjalnych)
Poprawka dynamiczna
Poprawka ortometryczna
Poprawka normalna
Definicja geoidy i quasigeoidy oraz ich związek z poszczególnymi systemami wysokości. Odchylenie linii od pionu i jej znaczenie w geodezji.
Geoida - Powierzchnia ekwipotencjalna, która zawiera w sobie swobodną powierzchnię oceanów. Geoida jako zerowa powierzchnia ekwipotencjalna przedstawia prawdziwy kształt (figurę) Ziemi.
Quasigeoida - nie jest powierzchnią ekwipotencjalną, lecz można ją jednoznacznie wyznaczyć. Na obszarze oceanów quasigeoida pokrywa się z geoidą, a pod lądami odstępy tych powierzchni nie przekraczają 2m.
Związki z poszczególnymi systemami wysokości:
wysokość ortometryczna = wysokość tego punktu ponad geoidą, liczoną wzdłuż linii siły ciężkości przechodzącej przez punkt P..
wysokość normalna = liczymy wzdłuż linii pionowej od quasigeoidy do danego punktu
wysokość dynamiczna=
Odchylenie linii od pionu= kąt między wektorami przyśpieszenia rzeczywistego i normalnego.
Rzut wektora na płaszczyznę I wertykału i południa astronomicznego wyznaczają składowe odchylenia pionu: wschodnią i północną. Inaczej , nazywamy składową odchylenia pionu w I wertykale, a składową południkową. Odchylenie pionu w dowolnym punkcie P zewnętrznego pola grawitacyjnego będzie zależało od przyjętej elipsoidy Uo = const potencjału normalnego U. Znaczy to, że linie siły ciężkości grawitacyjnych pól normalnych wytworzonych przez elipsoidę ziemską i elipsoidę odniesienia, które mają różne wielkości (a,α) i orientacje e bryle Ziemi, będą miały różne kierunki w punkcie P. Ponieważ wektor g jest jeden (praktycznie niezmienny) w punkcie P, więc odchylenie pionu między wektorem g a wektorami γ' - normalnego pola grawitacyjnego elipsoidy ziemskiej i γ - normalnego pola grawitacyjnego elipsoidy odniesienia będą różne.
Przez odchylenie linii pionu rozumiemy również kąt θ między prostą styczną do linii pionu w punkcie P a normalną do elipsoidy odniesienia. Ponieważ normalna do elipsoidy i styczna do linii siły ciężkości pola normalnego leżą w płaszczyźnie I wertykału wyraża się wzorem analogicznym jak składowa odchylenia pionu ϑ: η= (λ-L)cosB , a składowa ξ' odchylenia pionu θ w płaszczyźnir południka wyraża się wzorem:
ξ'=ϕ - B= ξ + 0,171”H sin 2B
gdzie H jest wyrażone w km.
Zewnętrzne pole grawitacyjne Ziemi, właściwości powierzchni ekwipotencjalnych.
Odchylenie pionu i jego znaczenie w pracach inżynierskich
Odchylenie linii od pionu= kąt między wektorami przyśpieszenia rzeczywistego i normalnego.
Rzut wektora na płaszczyznę I wertykału i południa astronomicznego wyznaczają składowe odchylenia pionu: wschodnią i północną. Inaczej , nazywamy składową odchylenia pionu w I wertykale, a składową południkową. Odchylenie pionu w dowolnym punkcie P zewnętrznego pola grawitacyjnego będzie zależało od przyjętej elipsoidy Uo = const potencjału normalnego U. Znaczy to, że linie siły ciężkości grawitacyjnych pól normalnych wytworzonych przez elipsoidę ziemską i elipsoidę odniesienia, które mają różne wielkości (a,α) i orientacje e bryle Ziemi, będą miały różne kierunki w punkcie P. Ponieważ wektor g jest jeden (praktycznie niezmienny) w punkcie P, więc odchylenie pionu między wektorem g a wektorami γ' - normalnego pola grawitacyjnego elipsoidy ziemskiej i γ - normalnego pola grawitacyjnego elipsoidy odniesienia będą różne.
Przez odchylenie linii pionu rozumiemy również kąt θ między prostą styczną do linii pionu w punkcie P a normalną do elipsoidy odniesienia. Ponieważ normalna do elipsoidy i styczna do linii siły ciężkości pola normalnego leżą w płaszczyźnie I wertykału wyraża się wzorem analogicznym jak składowa odchylenia pionu ϑ: η= (λ-L)cosB , a składowa ξ' odchylenia pionu θ w płaszczyźnir południka wyraża się wzorem:
ξ'=ϕ - B= ξ + 0,171”H sin 2B
gdzie H jest wyrażone w km.
Systemy wysokości
wysokość ortometryczna = wysokość tego punktu ponad geoidą, liczoną wzdłuż linii siły ciężkości przechodzącej przez punkt P..
wysokość normalna = liczymy wzdłuż linii pionowej od quasigeoidy do danego punktu
wysokość dynamiczna=
Omów system wysokości obowiązujący w Polsce i podaj zalety jego stosowania. Podaj ogólne zasady wyznaczania modelu Ziemi na danym obszarze np. w Polsce.
Wyjaśnij pojęcia: zewnętrzne i normalne pole grawitacyjne Ziemi, odchylenie pionu
Różnice między wysokością ortometryczną a normalną. Dlaczego przy ciągu niwelacji precyzyjnej I klasy o dł. 80 km stosujemy poprawkę normalną lub ortometryczną.
Opisać systemy wysokości.
Poprawki uwzględniane przy niwelacji precyzyjnej.
Wyjaśnij pojęcia : zewnętrzne i normalne pole grawitacyjne Ziemi; odchylenie pionu
Ⴗ
W=Wp=const
fiz. pow Ziemi
geoida
Wo
Ⴗ
Q
g
P
Ho
telluroida
fiz. pow Ziemi
Q
N
ξ
ξ
P
elipsoida
geoida
quasigeoida
W=Wp
Hp n
Hp