Statystyka - Materialy do zajec WER. 160510, Studia, Statystyka

1
R	Y_1p	X	Y_1K	G1
R	Y_2p	~X	Y_2K	G2
2
R		X	Y_1K	G1
R		~X	Y_2K	G2
3
R		X	Y_1K	G1
R	Y_2p	~X		G2
4	SOLOMONA
R	Y_1p	X	Y_1K	G1
R	Y_2p	~X	Y_2K	G2
R		X	Y_3K	G1
R		~X	Y_4K	G2

0x08 graphic

ISTOTNOŚĆ RÓŻNIC MIĘDZY DWIEMA ŚREDNIMI DLA PRÓB ZALEŻNYCH (TEST STUDENTA)

1.Wzór

0x08 graphic

gdzie: D = X₁ - X₂

2. Przykład:

a) tworzymy tabelę wg wzoru:

Lp.	X₁	X₂	D	D²
1	7	5	2	4
2	9	15	-6	36
3	4	7	-3	9
4	15	11	4	16
5	6	4	2	4
6	3	7	-4	16
7	9	8	1	1
8	5	10	-5	25
9	6	6	0	0
10	12	16	-4	16
Suma	76	89	-13	127
Średnia	7.6	8.9	-1.3

b) obliczamy wartość statystyki t:

0x08 graphic

c) obliczamy liczbę stopni swobody:

df = N - 1= 10 - 1 = 9

d) sprawdzamy w tabeli wartość krytyczną statystyki t dla obliczonej ilości stopni swobody (9) i przyjętego poziomu istotności α (najcześciej 0.05, test jednostronny):

t_df=9,_α_=0.05,jedn. = 1.833

e) sprawdzamy czy:

t	> t_df=9,_α_=0.05,jedn.

- w naszym przypadku:

-1.18

< 1.833,

- nie ma zatem podstaw do odrzucenia hipotezy zerowej: średnie dwóch pomiarów nie różnią się od siebie w sposób istotny.

WARTOŚCI KRYTYCZNE T

0x08 graphic

df	Poziom istotności przy teście jednostronnym
		0,10	0,05	0,025	0,01	0,005	0,0005
		Poziom istotności przy teście dwustronnym
		0,20	0,10	0,05	0,02	0,01	0,001
1	3,078	6,314	12,706	31,821	63,657	636,619
2	1,868	2,920	4,303	6,965	9,925	31,598
3	1,638	2,353	3,182	4,541	5,841	12,941
4	1,533	2,132	2,776	3,747	4,604	8,610
5	1,476	2,015	2,571	3,365	4,032	6,859
6	1,440	1,943	2,447	3,143	3,707	5,959
7	1,415	1,895	2,365	2,998	3,499	5,405
8	1,397	1,860	2,306	2,896	3,355	5,041
9	1,383	1,833	2,262	2,821	3,250	4,781
10	1,372	1,812	2,228	2,764	3,169	4,587
11	1,363	1,796	2,201	2,718	3,106	4,437
12	1,356	1,782	2,179	2,681	3,055	4,318
13	1,350	1,771	2,160	2,650	3,012	4,221
14	1,345	1,761	2,145	2,624	2,977	4,140
15	1,341	1,753	2,131	2,602	2,947	4,073
16	1,337	1,746	2,120	2,583	2,921	4,015
17	1,333	1,740	2,110	2,567	2,898	3,965
18	1,330	1,734	2,101	2,552	2,878	3,922
19	1,328	1,729	2,093	2,539	2,861	3,883
20	1,325	1,725	2,086	2,528	2,845	3,850
21	1,323	1,721	2,080	2,518	2,831	3,819
22	1,321	1,717	2,074	2,508	2,819	3,792
23	1,319	1,714	2,069	2,500	2,807	3,767
24	1,318	1,711	2,064	2,492	2,797	3,745
25	1,316	1,708	2,060	2,485	2,787	3,725
26	1,315	1,706	2,056	2,479	2,779	3,707
27	1,314	1,703	2,052	2,473	2,771	3,690
28	1,313	1,701	2,048	2,467	2,763	3,674
29	1,311	1,699	2,045	2,462	2,756	3,659
30	1,310	1,697	2,042	2,457	2,750	3,646
40	1,303	1,684	2,021	2,423	2,704	3,551
60	1,296	1,671	2,000	2,390	2,660	3,460
120	1,289	1,658	1,980	2,358	2,617	3,373
∞	1,282	1,645	1,960	2,326	2,576	3,291

Źródło: R.A. Fisher, F. Yates, Statistical tables for biological, agricultural, and medical research,

Edinburgh 1963, Oliver and Boyd.

0x08 graphic
ISTOTNOŚĆ ZWIĄZKU MIĘDZY DWIEMA ZMIENNYMI JAKOŚCIOWYMI (TEST CHI²)

1.Wzór:

= Σ(O - E)²/E,

gdzie:

O - liczebności zaobserwowane

E - liczebności oczekiwane

Otrzymaną wartość porównujemy z wartością krytyczną Chi² z tablic przy danym df

f_o

f_e

f_o - f_e

(f_o - f_e)²

(f_o - f_e)²/f_e

a+b

(a+b)*(a+c)/N

f_oa - f_ea

(f_oa - f_ea)²

(f_oa - f_ea)²/f_e_a

c+d

(a+b)*(b+d)/N

f_ob - f_eb

(f_ob - f_eb)²

(f_ob - f_eb)²/f_eb

a+c

b+d

(c+d)*(a+c)/N

f_oc - f_ec

(f_oc - f_ec)²

(f_oc - f_ec)²/f_ec

df = (w - 1)*(k - 1)

gdzie:

w - liczba wierszy

k - liczba kolumn

(c+d)*(b+d)/N

f_od - f_ed

(f_od - f_ed)²

(f_od - f_ed)²/f_ed

Σ [a,b,c,d]

CHI²=

Σ [(f_o - f_e)²/f_e]]

2. Przykład:

f_o

f_e

f_o - f_e

(f_o - f_e)²

(f_o - f_e)²/f_e

10.939

-3.939

15.519

1.419

8.061

3.939

15.519

1.925

8.061

3.939

15.519

1.925

df = (2 - 1)*(2 -1) = 1

5.939

-3.939

15.519

2.613

CHI²=

7.882

3,841

TEST ZNAKÓW DLA DWÓCH PRÓB NIEZALEŻNYCH

(TEST MEDIANY)

1.Wzór:
	-	+		f_o	f_e	f_o - f_e	(f_o - f_e)²	(f_o - f_e)²/f_e
1	a	b	a+b	a	(a+b)*(a+c)/N	f_oa - f_ea	(f_oa - f_ea)²	(f_oa - f_ea)²/f_ea
2	c	d	c+d	b	(a+b)*(b+d)/N	f_ob - f_eb	(f_ob - f_eb)²	(f_ob - f_eb)²/f_eb
	a+c	b+d	N	c	(c+d)*(a+c)/N	f_oc - f_ec	(f_oc - f_ec)²	(f_oc - f_ec)²/f_ec
				d	(c+d)*(b+d)/N	f_od - f_ed	(f_od - f_ed)²	(f_od - f_ed)²/f_ed
				Σ[a,b,c,d]			CHI²=	Σ[(f_o - f_e)²/f_e]]

2. Przykład:

lp	grupa	X	X_z
1	1	10	-
2	1	10	-
3	1	10	-
4	1	12	-
5	1	15	-
6	1	17	+
7	1	17	+
8	1	19	+
9	1	20	+
10	1	22	+
11	1	25	+
12	1	26	+
13	2	6	-
14	2	7	-
15	2	8	-
16	2	8	-
17	2	12	-
18	2	16	-
19	2	19	+
20	2	19	+
21	2	22	+
	Me =	16


	-	+		f_o	f_e	f_o - f_e	(f_o - f_e)²	(f_o - f_e)²/f_e
1	5	7	12	5	6.286	-1.286	1.653	0.263
2	6	3	9	7	5.714	1.286	1.653	0.289
	11	10	21	6	4.714	1.286	1.653	0.351
				3	4.286	-1.286	1.653	0.386
				21			CHI²=	1.289	<	3,841

TEST ZNAKÓW DLA DWÓCH PRÓB ZALEŻNYCH

0x08 graphic
(TEST ZNAKÓW FISHERA)

1.Wzór:

z = (IDI - 1)/N^0,5

gdzie:

D - różnica między liczba znaków "+" i "-"

N - liczba osób, dla których D <> 0

2. Przykład:

lp	grupa	X1	X2	R	X_z
1	1	15	19	-4	-
2	1	19	30	-11	-
3	1	31	26	5	+
4	1	36	8	28	+
5	1	10	10	0	0
6	1	11	6	5	+
7	1	19	17	2	+
8	1	15	13	2	+
9	1	10	22	-12	-
10	1	16	8	8	+
			liczba "+" =		6
			liczba "-" =		3
			IDI =		3

N = 9 (bo, jedna różnica = 0)

z = (3 -1)/9^0,5 = 0,67 < 1,96TEST RANG DLA DWÓCH PRÓB NIEZALEŻNYCH

(TEST SUMY RANG WILCOXONA, U MANNA-WHITNEYA 0x08 graphic
)

1.Wzór:

μ_R1= [N₁*(N₁ + N₂ + 1)]/2

σ_R1= ([N₁* N₂*(N₁ + N₂ + 1)]/12)^0,5

z = [I R₁ - μ_R1I - 0,5]/ σ_R1

gdzie:

N_1,N₂- liczba pomiarów w 1 i 2 grupie,

R₁- suma rang mniejszej próby

2. Przykład:

lp	grupa	x	x_r
1	1	27	5
2	1	33	7
3	1	37	8
4	1	52	13
5	1	53	14
6	1	57	16
7	1	69	18
8	1	70	19
9	1	71	20
10	1	77	22
11	2	6	1
12	2	9	2
13	2	14	3
14	2	16	4
15	2	29	6
16	2	43	9
17	2	45	10
18	2	47	11
19	2	50	12
20	2	55	15
21	2	63	17
22	2	72	21
		R1=	142

N₁ = 10

N₂ = 12

μ_R1= (10*(10 + 12 + 1))/2 = 115

σ_R1= [(10*12(10 + 12 + 1))/12]^0,5 = 15,16575

z = [I 142 - 115I - 0,5]/ 15,16575 = 1,747 < 1,96

TEST RANG DLA DWÓCH PRÓB ZALEŻNYCH

(TEST ZNAKÓW RANGOWYCH WILCOXONA 0x08 graphic
)

1.Wzór:

μ_W+= [N*(N + 1)]/4

σ_W+= ([N*(N + 1)*(2N + 1)]/24)^0,5

z = (W₊ - μ_W+)/ σ_W+

gdzie:

N- liczba pomiarów,

W₊- suma rang dodatnich

2. Przykład:

lp	grupa	x1	x2	D	W
1	1	15	19	-4	-3
2	1	19	30	-11	-7
3	1	31	26	5	4,5
4	1	36	8	28	9
5	1	10	10	0
6	1	11	6	5	4,5
7	1	19	17	2	1,5
8	1	15	13	2	1,5
9	1	10	22	-12	-8
10	1	16	8	8	6
				W₊=	27

N = 9

μ_W+= 9*(9 + 1)/4 = 22,5

σ_W+= [(9*(9 + 1)*(2*9 +1))/24]^0,5 = 8,441

z = (27 - 22,5)/ 8,441 = 0,533 < 1,96

REGRESJA LINIOWA 0x08 graphic
I
WSPÓŁCZYNNIK KORELACJI PEARSONA

1.Wzory:

b_yx= (NΣXY - ΣXΣY)/(NΣX² - (ΣX)²)

a_yx = (ΣY - b_yxΣX)/N

r_xy= (NΣXY - ΣXΣY)/[(NΣX² - (ΣX)²)*(NΣY² - (ΣY)²)]^0,5

t = r*[(N - 2)/(1 - r²)]^0,5 (istotność wsp. korelacji)

df = N - 2;

2. Przykład:

Lp.	X	Y	X²	Y²	XY
1	5	1	25	1	5
2	10	6	100	36	60
3	5	2	25	4	10
4	11	8	121	64	88
5	12	5	144	25	60
6	4	1	16	1	4
7	3	4	9	16	12
8	2	6	4	36	12
9	7	5	49	25	35
10	1	2	1	4	2
Suma	60	40	494	212	288
	ΣX	ΣY	ΣX²	ΣY²	ΣXY

b_yx= (10*288 -60*40)/(10*494 - (60)²) = 0,358

a_yx = (40 - 0,358*60)/10 = 1,852

r_xy= (10*288 -60*40)/[(10*494 - (60)²)*(10*212 - (40)²)]^0,5= 0,575

t = 0,575*[(10 - 2)/(1 - 0,575²)]^0,5 = 1,987 < 2,306

0x08 graphic
ISTOTNOŚĆ RÓŻNIC MIĘDZY DWIEMA ŚREDNIMI DLA PRÓB NIEZALEŻNYCH (TEST STUDENTA)

1.Wzór

0x08 graphic

s² = [Σ_n1X² - (Σ_n1X)²/N₁ + Σ_n2X² - (Σ_n2X)²/N₂]/(N₁ + N₂ - 2)

df = N₁ + N₂ - 2

2. Przykład:

a) tworzymy tabelę wg wzoru:

Lp.	GR	X	X²	obliczenia
1	1	16	256
2	1	9	81
3	1	4	16	N1	=	8
4	1	23	529	N2	=	6
5	1	19	361	Σ_n1X	=	88
6	1	10	100	Σ_n2X	=	48
7	1	5	25	X₁	=	11
8	1	2	4	X₂	=	8
9	2	20	400	Σ_n1X²	=	1372
10	2	5	25	Σ_n2X²	=	702
11	2	1	1
12	2	16	256
13	2	2	4
14	2	4	16

b) obliczamy wartość s²:

0x08 graphic

c) obliczamy wartość statystyki t:

0x08 graphic

d) sprawdzamy w tabeli wartość krytyczną statystyki t dla obliczonej ilości stopni swobody (12) i przyjętego poziomu istotności α (najcześciej 0.05, test dwustronny):

t_df=12,_α_{=0.05,dwustr.} = 2.179

e) sprawdzamy czy:

t	> t_df=12,_α_{=0.05,dwustr.}

- w naszym przypadku:

0.72

< 2.179,

- nie ma zatem podstaw do odrzucenia hipotezy zerowej: średnie dwóch pomiarów nie różnią się od siebie w sposób istotny.

0x08 graphic
WSPÓŁCZYNNIK KORELACJI PEARSONA

(WZÓR 1)

1.Wzór:

r_xy= [Σ(z_X*z_Y)]/(N - 1)

2. Przykład:

Lp.	X	Y	(X - M_x)²	(Y - M_y)²	z_x	z_y	z_x*z_y
1	5	1	1	9	-0,259	-1,248	0,323
2	10	6	16	4	1,037	0,832	0,863
3	5	2	1	4	-0,259	-0,832	0,216
4	11	8	25	16	1,296	1,664	2,156
5	12	5	36	1	1,555	0,416	0,647
6	4	1	4	9	-0,518	-1,248	0,647
7	3	4	9	0	-0,777	0,000	0,000
8	2	6	16	4	-1,037	0,832	-0,863
9	7	5	1	1	0,259	0,416	0,108
10	1	2	25	4	-1,296	-0,832	1,078
Suma	60	40	134	52			5,175
	ΣX	ΣY	Σ(X - M_x)²	Σ(Y - M_y)²			Σz_x*z_y
	M_x	M_y	S_x	S_y			r_xy
	6,000	4,000	3,859	2,404			0,575

r_xy= (5,17523)/(10 -1)= 0,575

STATYSTYKA OPISOWA 0x08 graphic

1. Tablice frekwencji, przedziały klasowe.

Dla prób o dużej liczebności (n >= 30) elementy próby grupuje się w klasach, tj. przedziały o równej długości.

Reguły ustalenia liczby klas (k) i ich długości:

a) k ≤ 5*lg(n)

b) k = 1+ 3.32*lg(n)

c) k =

d) k ∈ <10; 20>

e) przedziały klasowe równe 1, 3, 5, 10 lub 20 pkt.

f) długość klasy b ≅ R/k, gdzie R = x_max- x_min.

Przedział klasowy powinien zaczynać się od wartości, która stanowi wielokrotność rozmiaru tego przedziału

Przedziały klasowe powinny być posortowane malejąco.

Niech n_i- liczność i-tej klasy, a
środek i-tej klasy. Wtedy pary liczb (
, n_i) nazywamy szeregiem rozdzielczym.

Graficzne przedstawienie szeregu rozdzielczego nazywa się histogramem.

2. Miary tendencji centralnej

A. Średnia

Średnia arytmetyczna
liczb x₁, x₂, x₃,...x_n określona jest wzorem

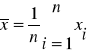
0x01 graphic

Charakterystyczna własność średniej arytmetycznej: suma wszystkich odchyleń jest równa zero;
.

Średnia geometryczna
liczb dodatnich określona jest wzorem

Średnia harmoniczna
, różnych od zera liczb x₁, x₂, x₃,...x_n,, nazywamy odwrotność średniej arytmetycznej odwrotności tych liczb

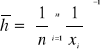
0x01 graphic

B. Mediana

Mediana (wartość środkowa) m_e - środkowa liczba w uporządkowanej niemalejąco próbce (dla próbki o liczności nieparzystej) lub średnią arytmetyczną dwóch liczb środkowych (dla próbki o liczności parzystej).

0x08 graphic
STATYSTYKA OPISOWA (c.d.)

C. Modalna

Wartością modalną (modą, dominantą) m₀ próby o powtarzających się wartościach nazywamy najczęściej powtarzającą się wartość, o ile istnieje, nie będącą x_min ani x_max.

3. Miary rozproszenia

A . Rozstęp R

R = x_max- x_min

B. Wariancja s²

Średnia arytmetyczna kwadratów odchyleń poszczególnych wartości x_i od średniej arytmetycznej

C. Odchylenie standardowe

D. Odchylenie przeciętne d₁ od wartości średniej

Średnia arytmetyczna wartości bezwzględnych odchyleń poszczególnych wartości x_i od średniej arytmetycznej

E. Odchylenie przeciętne d₂ od mediany

Średnia arytmetyczna wartości bezwzględnych odchyleń poszczególnych wartości x_i od mediany m_e

0x08 graphic
WYNIK STANDARYZOWANY, SKALE STANDARDOWE

0x08 graphic

wynik standaryzowany:

Typowe skale stosowane przy normach opartych o rozkład normalny:

T = 10z + 50; zasięg: < -5; 5 >

sten = 2z + 5,5; zasięg: < -2,25; 2,25 >

stanin = 2z + 5; zasięg: < -2; 2 >

IQ Wechslera = 15z + 100; zasięg: < -4; 4 >

tetron = 4z + 10; zasięg: < -2,5; 2,5 >

CECHY ROZKŁADU NORMALNEGO

Wzór: 0x08 graphic

gdzie:

f(x) - oznaczana wysokość krzywej rozkładu dla wartości zmiennej niezależnej X,

exp[...] - podstawa logarytmu naturalnego (e ≈ 2,7182) podniesiona do potęgi [...],

 - „pi” - stała matematyczna;  ≈ 3,14159,

 - wartość średnia,

σ - odchylenie standardowe,

Cechy rozkładu normalnego:

kształt krzywej normalnej zależy od: a) średniej arytmetycznej b) odchylenia standardowego; wartość  determinuje położenie wartości maksymalnej na osi zmiennej niezależnej, zaś wartość σ określa stopień spłaszczenia krzywej,

powierzchnia pod krzywą rozkładu standaryzowanego jest równa jedności,

rozkład jest symetryczny o najwyższej wartości Y dla pomiaru X równego wartości średniej ,

zmienna X może przyjmować wartości z przedziału (-, +),

wszystkie wartości Y są dodatnie,

około 68,26% powierzchni pod krzywą zawarte jest w przedziale jednego odchylenia standardowego od wartości średniej,

około 95,46% powierzchni pod krzywą zawarte jest w przedziale dwóch odchyleń standardowych od wartości średniej,

około 99,73% powierzchni pod krzywą zawarte jest w przedziale trzech odchyleń standardowych od wartości średniej

s₁ ≠ s₂ ≠ s₃;
₁ =
₂ =
₃

0x01 graphic

ISTOTNOŚĆ RÓŻNIC DLA JEDNEJ PRÓBY

(TEST STUDENTA)

0x08 graphic

1.Wzór

0x08 graphic

df = N - 1

2. Przykład:

a) tworzymy tabelę wg wzoru:

Lp.	X		(X - M)²
1	7		0,36	μ = 5,295
2	9		1,96
3	4		12,96
4	15		54,76
5	6		2,56
6	3		21,16
7	9		1,96
8	5		6,76
9	6		2,56
10	12		19,36
M =	7,600	s =	3,718

b) obliczamy wartość statystyki t:

0x08 graphic

c) obliczamy liczbę stopni swobody:

df = N - 1 = 10 - 1 = 9

d) sprawdzamy w tabeli wartość krytyczną statystyki t dla obliczonej ilości stopni swobody (9) i przyjętego poziomu istotności α (najcześciej 0.05, test dwustronny):

t_df=9_,_α_{=0.05,dwustr.} = 2.262

e) sprawdzamy czy:

t	> t_df=9_,_α_{=0.05,dwustr.}

- w naszym przypadku:

1.961

< 2,262

- nie ma zatem podstaw do odrzucenia hipotezy zerowej: próba pochodzi z populacji generalnej o średniej 5,295

X₁i X₂oznaczają odpowiednio pierwszy i drugi pomiar zmiennej

ΣD x

√[NΣD² - (ΣD)²]/(N - 1)

t =

- 13 x

√[10 x 127 - (-13)²]/(10 - 1)

= -1.18

wartość krytyczna

t z przykładu

(df = 9; α = 0.05;

t. jednostronny)

= a

= b

= c

= d

= 0,72

t =

11 - 8 x

√ 60,17/8 + 60,17/6

= 60,17

s² =

1372 - 88²/8 + 702 - 48²/6

8 + 6 - 2

t =

X₁ - X₂ x

√s²/N₁ + s²/N₂

M - μ x

√s²/N

t =

7,6 - 5,295 x

√ 3,718²/10

t =

= 1,961