Ćwiczenie nr 15/16
Temat: Wyznaczanie współczynnika lepkości metodą Stokesa oraz metodą Hopplera.
I. Metoda Stokesa.
1. Opis teoretyczny.
Lepkością lub tarciem wewnętrznym nazywamy zjawisko występowania sił stycznych przeciwstawiających się przemieszczeniu jednych części ciała względem innych jego części. Wskutek tarcia występującego między cząsteczkami cieczy lub gazu, poruszająca się cząstka pociąga za sobą cząsteczki sąsiadujące z nią z prędkością tym bardziej zbliżoną do prędkości własnej, im ciecz lub gaz są bardziej lepkie. Analogicznie cząsteczka spoczywająca hamuje poruszające się cząsteczki sąsiednie. Ze względu na to, że wszystkie rzeczywiste ciecze i gazy są lepkie zjawisko lepkości odgrywa istotną rolę podczas przepływu cieczy oraz podczas ruchu ciała stałego w ośrodku ciekłym.
Ciało stałe, poruszające się w ośrodku ciekłym, napotyka na opór. W otoczeniu ciała obserwujemy wtedy ruch cieczy. Mechanizm tego zjawiska jest następujący : warstwa cieczy, przylegająca do powierzchni poruszającego się ciała, wprawia w ruch pozostałe warstwy cieczy. Tak więc istotną rolę odgrywa tu lepkość cieczy. Dla ciał o symetrii osiowej poruszającego się w kierunku osi, wypadkowa siła oporu działa przeciwstawnie do kierunku ruchu. Doświadczalnie stwierdza się, że dla małych prędkości siła tarcia wewnętrznego R jest wprost proporcjonalna do prędkości v. Poza tym zależy ona od charakterystycznego wymiaru liniowego ciała l oraz od współczynnika lepkości cieczy .
Równanie określające siłę oporu (tarcia wewnętrznego ma postać:
Fl= - K l v
gdzie K jest to stała zależna od kształtu ciała.
Współczynnik lepkości cieczy η jest to stosunek ciśnienia stycznego p wywołującego przesuwanie się jednych warstw cieczy po drugich do gradientu (spadku) prędkości V w cieczy ![]()
.
Dla kuli mamy K= 6 i równanie przechodzi w tzw. prawo Stokesa:
Fl = 6 r v
W miarę wzrastania prędkości, zgodnie z prawem Stokesa, opór lepkości
coraz bardziej rośnie i w pewnej chwili siła ciężkości staje się równa sumie Fl + Fw
Fw=Vρcg
gdzie:
ρc -gęstość cieczy (ośrodka)
Warunek równowagi sił ma postać:
mg = 6πrn + Vρcg
skąd:
![]()
Powyższe równanie jest słuszne jedynie w zastosowaniu do cieczy nieskończenie rozciągłych tzn. znajdujących się w bardzo szerokich naczyniach. Jeżeli kulka spada w rurze cylindrycznej o promieniu R, występujące wówczas pływy zmniejszają prędkość spadania i do powyższego wzoru należy wprowadzić czynnik korekcyjny zależny od stosunku r/R. Otrzymujemy wówczas skorygowany wzór:
2. Metoda pomiaru wiskozymetrem Stokesa.
W doświadczeniu stosujemy wiskozymetr Stokesa. Stanowią go dwa dość wysokie cylindryczne naczynia szklane, wstawione jedno w drugie. Przestrzeń między jednym cylindrem a drugim wypełniona jest wodą, którą można podgrzewać za pomocą grzejnika elektrycznego E, odczytując temperaturę na termometrze T1. Ciecz badaną nalewamy do cylindra wewnętrznego, na którym zaznaczone poziome kreski P1, P2, P3 służące za wskaźniki odniesienia przy mierzeniu drogi, jaką przebywa spadająca kulka. Temperaturę cieczy podaje termometr T, a mieszadełka M1 i M2 pomagają w wyrównaniu temperatury kąpieli wodnej i badanej cieczy.
II. Metoda Hopplera.
1. Metoda pomiaru wiskozymetrem Hopplera.
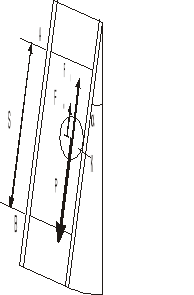
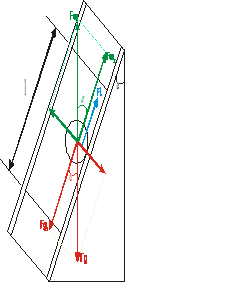
W tym przyrządzie znaczne spowolnienie spadającej kulki zostało uzyskane w następujący sposób. Kulka szklana lub metalowa o średnicy rzędu 10-20 mm spada w kalibrowanej rurce szklanej wypełnionej cieczą; średnica rurki jest zbliżona do rozmiarów kulki. Dla uniknięcia zakłóceń ruchu (wibracji) kulki rurka jest nieznacznie nachylona do pionu. W takich warunkach kulka jest przyciskana jedną składową siły ciężkości do ścianki rurki, druga składowa P' powoduje toczenie się kulki po ściance (w rzeczywistości po cienkiej warstewce cieczy, wyściełającej ściankę).
Rurka z badaną cieczą (olej z oliwek) jest zakończona bańką szklaną częściowo wypełnioną powietrzem. Duża ściśliwość powietrza zamkniętego amortyzuje termiczne zmiany objętości cieczy w rurce. Rurka ta umieszczona jest w naczyniu stanowiącym płaszcz włączony w obieg ultratermostatu. Dzięki czemu istnieje możliwość zmiany i utrzymania stałej wartości temperatury badanej cieczy. Naczynie ma możliwość zmiany położenia poprzez obrót o kąt 180° wokół osi przy zachowaniu stałego nachylenia rurki pomiarowej. Pozwala to mierzyć czas opadania kulki w obydwu kierunkach. Czas opadania kulki mierzony jest elektronicznie przy użyciu dwóch czujników fotoelektrycznych odpowiednio rozmieszczonych i oddalonych od siebie na odległość stanowiącą odcinek drogi przebywany przez kulkę ruchem jednostajnym.
2. Opis teoretyczny
Rurka z badaną cieczą stanowi równię pochyła o kącie nachylenia ok. 30°, w której stacza się swobodnie kulka stalowa o średnicy mniejszej od średnicy rurki. Toczenie się kulki w cieczy ulega znacznemu zwolnieniu gdy średnica wewnętrzna rurki różni się nieznacznie od średnicy kulki. Rurka powinna być ukośna, gdyż przy pionowym ustawieniu ruch kulki nie jest jednostajny. Przy ustawieniu ukośnym rurki, kulka toczy się po jej ściance. Do omawianego przypadku stosuje się wzór:
![]()
gdzie:
![]()
- dynamiczny współczynnik lepkości
k- stała przyrządu
![]()
- gęstość kulki
![]()
- gęstość płynu
t- czas opadania kulki
Współczynnik lepkości zależy w dużym stopniu
od temperatury. Zależność tą opisuje równanie:
![]()
T - temperatura w skali Kelvina
A, B - stałe charakteryzujące ciecz
Siła Fl jest skierowana przeciwnie do prędkości v toczenia się kulki. Zarówno Fl jak i v są nachylone do pionu pod kątem α. Na kulkę działają, podobnie jak w wiskozymetrze Stokesa, trzy siły: składowa P' siły ciężkości (rzut P na kierunek osi rurki), składowa siły wyporu F'w (rzut Fw na kierunek osi rurki), siła oporu lepkości. W przypadku ruchu jednostajnego kulki mamy do czynienia z równowagą tych sił, której wyrazem jest równość:
mgcosα - Fwcosα = krvη.
III. Wyprowadzenie wzorów roboczych.
1) Stokesa
Zakładając, że F=0 oraz v=l/t gdzie t - czas spadania kulki na drodze l, otrzymamy:
2) Hopplera
Zakładając, że F=0 oraz v=l/τ gdzie τ - czas spadania kulki na drodze l, otrzymamy:
V. Opis przeprowadzonego eksperymentu
Metoda Stokesa
Do wykonania eksperymentu użyłem dziesięciu ołowianych kulek o niewielkiej średnicy. Za pomocą śruby mikrometrycznej wyznaczyłem średnicę każdej kulki. Następnie wypuszczałem je kolejno przez lejek. W chwili gdy kulka przekroczyła krawędź górnego pierścienia włączyłem sekundomierz, a gdy kulka przekroczyła krawędź dolną - zatrzymałem go. Następnie notowałem czas przybycia odległości l (uprzednio zmierzonej za pomocą miarki milimetrowej) dla poszczególnych kulek. Po czym wyznaczyłem współczynniki lepkości dla każdej kulki korzystając ze wcześniej wyprowadzonego wzoru. Następnie korzystając ze wzoru na średnią arytmetyczną wyznaczyłem średni współczynnik lepkości badanej cieczy.
2) Metoda Hopplera
Przed przystąpieniem do pomiarów należało wypoziomować przyrząd. Następnie odczytałem temperaturę T1. Cykl pomiarowy polegał na pomiarze czasu w jakim kulka przebyła drogę l od punktu A do B. Pomiar ten był powtarzany dwadzieścia razy, a następnie po zakończeniu obserwacji odczytałem temperaturę T2. Korzystając z zależności
T=0,5(T1+ T2) wyznaczyłem średnią temperaturę, a w dalszej kolejności średni czas opadania kulki. Wykorzystując wyprowadzony wzór roboczy wyznaczyłem współczynnik lepkości.
VI. Obliczenia i wyznaczanie niepewności.
Metoda Stokesa
|
∅ [mm] |
r [m] |
t [s] |
ρk [kg/m3] |
ρc [kg/m3] |
g [m/s2] |
l [m] |
η [kg/m*s] |
1 |
3,08 |
0,00154 |
2,31 |
11370 |
1250 |
9,81 |
0,572 |
0,21129752 |
2 |
3,15 |
0,001575 |
2,22 |
11370 |
1250 |
9,81 |
0,572 |
0,212400272 |
3 |
3,1 |
0,00155 |
2,41 |
11370 |
1250 |
9,81 |
0,572 |
0,22331681 |
4 |
3,02 |
0,00151 |
2,3 |
11370 |
1250 |
9,81 |
0,572 |
0,202265917 |
5 |
3,08 |
0,00154 |
2,34 |
11370 |
1250 |
9,81 |
0,572 |
0,214041643 |
6 |
3,1 |
0,00155 |
2,35 |
11370 |
1250 |
9,81 |
0,572 |
0,217757056 |
7 |
3,06 |
0,00153 |
2,54 |
11370 |
1250 |
9,81 |
0,572 |
0,229328249 |
8 |
3,09 |
0,001545 |
2,34 |
11370 |
1250 |
9,81 |
0,572 |
0,21543378 |
9 |
3,11 |
0,001555 |
2,28 |
11370 |
1250 |
9,81 |
0,572 |
0,21263591 |
10 |
3,11 |
0,001555 |
2,4 |
11370 |
1250 |
9,81 |
0,572 |
0,223827274 |
ti [s] |
|
|
2,31 |
0,039 |
0,001521 |
2,22 |
0,129 |
0,016641 |
2,41 |
-0,061 |
0,003721 |
2,3 |
0,049 |
0,002401 |
2,34 |
0,009 |
8,1E-05 |
2,35 |
-0,001 |
1E-06 |
2,54 |
-0,191 |
0,036481 |
2,34 |
0,009 |
8,1E-05 |
2,28 |
0,069 |
0,004761 |
2,4 |
-0,051 |
0,002601 |
|
|
|
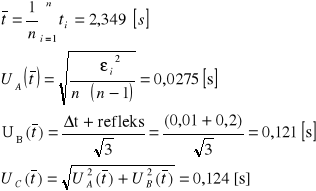
R [m] |
|
|
0,00154 |
5E-06 |
2,5E-11 |
0,001575 |
-3E-05 |
9E-10 |
0,00155 |
-5E-06 |
2,5E-11 |
0,00151 |
3,5E-05 |
1,23E-09 |
0,00154 |
5E-06 |
2,5E-11 |
0,00155 |
-5E-06 |
2,5E-11 |
0,00153 |
0,000015 |
2,25E-10 |
0,001545 |
0 |
0 |
0,001555 |
-1E-05 |
1E-10 |
0,001555 |
-1E-05 |
1E-10 |
|
|
|
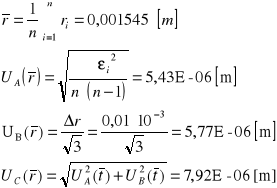
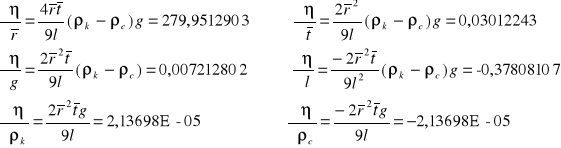
Metoda Hopplera
Nr |
τ [s] |
|
|
1 |
10,60 |
-0,254 |
0,064516 |
2 |
10,35 |
-0,004 |
1,6E-05 |
3 |
10,30 |
0,046 |
0,002116 |
4 |
10,40 |
-0,054 |
0,002916 |
5 |
10,40 |
-0,054 |
0,002916 |
6 |
10,40 |
-0,054 |
0,002916 |
7 |
10,50 |
-0,154 |
0,023716 |
8 |
10,27 |
0,076 |
0,005776 |
9 |
10,37 |
-0,024 |
0,000576 |
10 |
10,35 |
-0,004 |
1,6E-05 |
11 |
10,32 |
0,026 |
|
12 |
10,38 |
-0,034 |
0,001156 |
13 |
10,22 |
0,126 |
0,015876 |
14 |
10,35 |
-0,004 |
1,6E-05 |
15 |
10,35 |
-0,004 |
1,6E-05 |
16 |
10,19 |
0,156 |
0,024336 |
17 |
10,32 |
0,026 |
0,000676 |
18 |
10,28 |
0,066 |
0,004356 |
19 |
10,22 |
0,126 |
0,015876 |
20 |
10,35 |
-0,004 |
1,6E-05 |
|
|
|
|
![]()
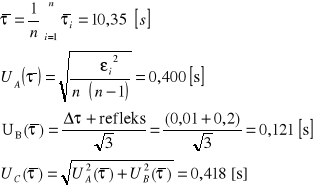
![]()
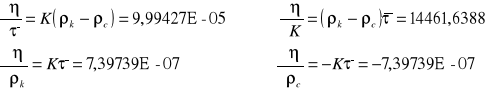
IVa. Korekta szacowania niepewności pomiaru współczynnika lepkości metodą Stokesa
Lp. |
|
|
1 |
0,21129752 |
0,000024649 |
2 |
0,212400272 |
0,000014915 |
3 |
0,22331681 |
0,000049765 |
4 |
0,202265917 |
0,0001959 |
5 |
0,214041643 |
0,000004931 |
6 |
0,217757056 |
0,000002234 |
7 |
0,229328249 |
0,000170717 |
8 |
0,21543378 |
0,000000686 |
9 |
0,21263591 |
0,000013151 |
10 |
0,223827274 |
0,00057227 |
|
0,001049218 |
|
![]()
Fl
v
mg
Fw
Fl
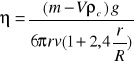
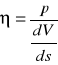
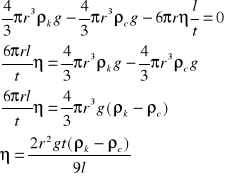
![]()
Fg
Fw
Fl
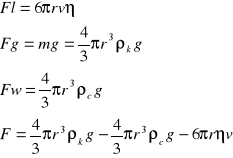
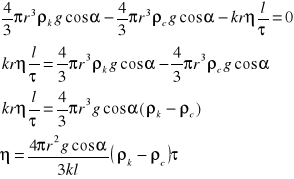
![]()
![]()
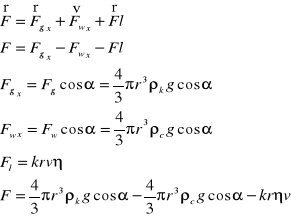
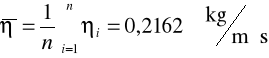
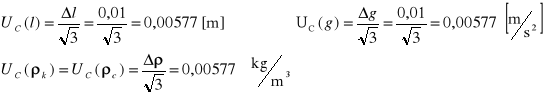
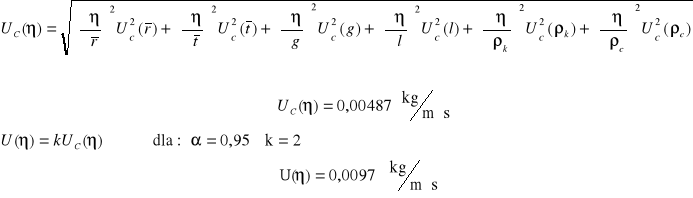
![]()
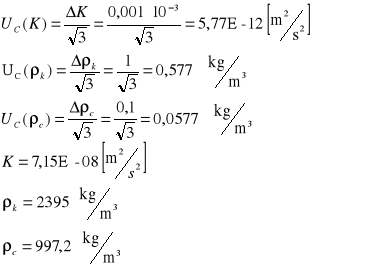
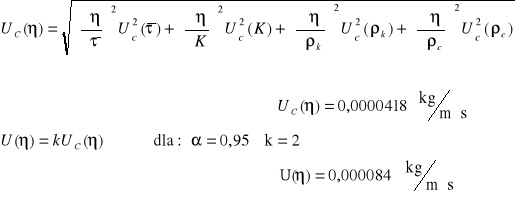
![]()
![]()
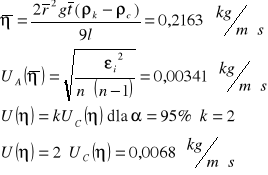
Wyszukiwarka
Podobne podstrony:
I 1224
1224
1224
1224
1224
Instalacja elektryczna Ursus 912 914 1012 1014 1222 1224 1614 1929
1224
UKIE - transp-1224
1224
Ursus 912, 914, 1012, 1014, 1222, 1224, 1614, kabina kierowcy
1224
Roscadora 1224
Jak podłączyć wskaźnik poziomu paliwa w URSUSIE C 385 902 904 912 914 1002 1004 1012 1014 1212 1214
Ursus 1222, 1224, 1614
Instalacja elektryczna Ursus 912 914 1012 1014 1222 1224 1614 1929
Jak podłączyć wskaźnik poziomu paliwa w URSUSIE C 385 902 904 912 914 1002 1004 1012 1014 1212 1214
więcej podobnych podstron