Siły zewnętrzne - siły czynne, czyli obciążenia oraz siły bierne zwane reakcjami, działające z zewnątrz na dane ciało.
Siły wewnętrzne - siły spójności, jakimi odcięte części ciała oddziałują na siebie wzajemnie.
Sztywność konstrukcji - sztywność każdej konstrukcji opisują odkształcenia, które dla zachowania sztywności konstrukcji, nie mogą przekraczać odkształceń dopuszczalnych.
Stateczność konstrukcji - każda konstrukcja powinna spełniać warunek stateczności, czyli powinna być w równowadze, niezależnie od tego czy dany element konstrukcji jest poddawany obciążeniom czy nie.
Nośność konstrukcji - nośność konstrukcji wiąże się z wytrzymałością konstrukcji na naprężenia. Każda konstrukcja ma określone dopuszczalne naprężenia, mogą to być: dopuszczalne naprężenia na rozciąganie, skręcanie lub zginanie. Dlatego, aby warunek nośności był spełniony naprężenia, zarówno normalne jak i styczne, nie mogą przekraczać tych wartości.
Rozciąganie (ściskanie) - siłą wewnętrzną występującą przy rozciąganiu (ściskaniu) jest siła normalna. Jest ona skierowana prostopadle do przekroju poprzecznego pręta wywołując jego rozciąganie lub ściskanie.
Zginanie - siły wewnętrzne występujące przy zginaniu belki to siły tnące i momenty gnące. Siłą tnącą nazywamy składową - prostopadłą do osi belki - geometrycznej wszystkich sił działających na część belki, znajdującą się po jednej stronie rozpatrywanego przekroju. Momentem gnącym nazywamy sumę geometryczną momentów wszystkich sił zewnętrznych działających na część belki, znajdującą się po jednej stronie rozpatrywanego przekroju.
Skręcanie - siłą wewnętrzną przy skręcaniu są momenty skręcające. Moment skręcający nazywamy sumę algebraiczną momentów wszystkich par sił zewnętrznych, działających po jednej stronie rozpatrywanego przekroju i leżących w płaszczyznach prostopadłych do osi pręta.
Co nazywamy naprężeniem? Od czego zależy wartość naprężenia i ile może być składowych naprężenia?
Naprężenie jest miarą gęstości sił wewnętrznych, ściśle wiąże się z odkształceniami. Wartość naprężenia zależy od wartości przyłożonej siły, a także od kątu pod jakim ta siła działa na zadany przekrój. Rozróżniamy dwie składowe naprężenia: naprężenia normalne - skierowane prostopadle do myślowego przekroju, wywołuje oderwanie się od siebie sąsiednich warstw przekroju, naprężenia styczne - wywołuje przesunięcie, a więc poślizg sąsiednich warstw przekroju.
W jakim wyrażeniu występuje sztywność na rozciąganie lub ściskanie? Podać orientacyjną wartość modułu Younga dla stali niskowęglowej.
Sztywność na rozciąganie lub ściskanie występuje w II postaci prawa Hooke'a, które opisuje wzór:
σ
σ naprężenie
, Pa moduł Younga
Co to jest względne wydłużenie? Omówić II postać prawa Hooke'a.
Względne wydłużenie jest wprost proporcjonalne do wydłużenia pręta i odwrotnie proporcjonalne do jego długości początkowej(II prawo Hooke'a). II postać prawa Hooke'a mówi, że wartość naprężenia normalnego do przekroju jest proporcjonalna do wartości względnego wydłużenia w kierunku prostopadłym do tego przekroju. Prawo te obowiązuje w zakresie sprężystości materiału.
Podać warunek wytrzymałościowy dla elementów rozciąganych. Na czym polega obliczenie wartości naprężeń oraz całkowitego wydłużenia prętów o dowolnych przekrojach poprzecznych?
Warunek wytrzymałościowy dla elementów rozciąganych: Zarówno naprężenia normalne σ jak i naprężenia styczne nie mogą przekraczać naprężeń dopuszczalnych na rozciąganie. Obliczenie wartości naprężeń oraz całkowitego wydłużenia prętów polega przeprowadzeniu próby rozciągania, podczas której badaną próbkę materiału poddaje się obciążeniom. Podczas próby obserwuje się na bieżąco zmiany. Po zakończonej próbie porównuje się próbki sprzed jak i po przeprowadzeniu próby rozciągania.
Narysować wykres rozciągania i omówić fazy próby rozciągania.
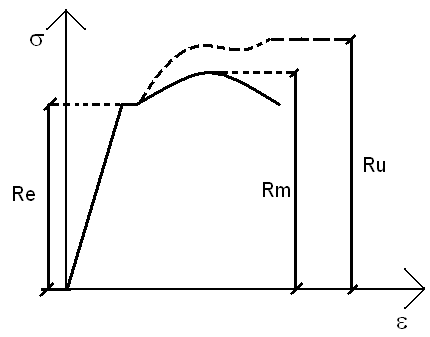
Statyczna próba rozciągania
Re - granica plastyczności
Rm - granica wytrzymałości na rozciąganie
Ru - naprężenie zrywające
Początkowo wykres ma charakter linii prostej nachylonej pod kątem, którego tangens jest równy modułowi Younga. Tę wartość naprężenia i odpowiadające jej wydłużenie próbki nazwano granicą proporcjonalności. Zwiększając obciążenie zauważamy, że wykres przestaje być linią prostą, przechodząc w linię krzywą. Na tym etapie widać wyraźny wzrost wydłużenia. Takie zjawisko wyraźnego wzrostu wydłużenia przy niezmiennej sile jest charakterystyczne dla materiałów plastycznych. Dlatego też odpowiadające mu obciążenie nazwano granicą plastyczności. Po przekroczeniu granicy plastyczności obserwujemy dalszy wzrost siły i towarzyszący mu wzrost wydłużenia według linii krzywej, która w pewnym miejscu osiąga ekstremum, po czym zaczyna znów opadać, aby urwać się gwałtownie, w tym momencie próbka pęka. Obciążenie odpowiadające ekstremum nazwano wytrzymałością na rozciąganie, a siłę, przy której następuję pęknięcie próbki nazwano naprężeniem zrywającym.
Rozciągany pryzmatyczny pręt o przekroju F=4cm2 wykonany ze stali niskowęglowej wykazuje wydłużenie =0.025%. Jakie jest naprężenie w pręcie i jaka jest siła rozciągająca pręt?
Dane: Szukane:
F=4cm2=0,0004m2 σ
,, P=?
,Pa
σ
σ,Pa *0,00025=52,5MPa
P=σF=52,5*106N/m2 * 4*10-4m2=21kN
Jaki jest moduł sprężystości i liczba Poissona materiału pręta o przekroju kwadratowym (F=4cm2), który przy osiowym ściskaniu siłą P=60kN skrócił się na długość l=10cm o l=0.210mm, a którego bok kwadratu wydłużył się o 0.014mm?
Podać zależności opisujące naprężenia w przekroju ukośnym osiowo rozciąganej próbki. Jakie wnioski wynikają z tych wzorów?
σσxcos2
,σxsin2
Wnioski dla naprężeń normalnych:
naprężenia normalne osiągają największą wartość w przekroju poprzecznym rozpatrywanego przekroju poprzecznym rozpatrywanego elementu, malej ze zwiększeniem kąta i są równe zeru dla ,
naprężenia normalne w dwóch wzajemnie równoległych przekrojach są sobie równe,
przekroje, w których naprężenia normalne osiągają ekstremum są do siebie prostopadłe,
na kierunku działania obciążeń zewnętrznych tj. występują jedynie naprężenia normalne.
Wnioski dla naprężeń stycznych:
naprężenie styczne rosną ze zwiększeniem kąta i osiągają maksymalna wartość max=0,5σx dla , a następnie maleją i są równe zeru dla ,
naprężenie styczne w dwóch wzajemnie prostopadłych przekrojach są sobie równe, co do wartości bezwzględnej i są skierowane do lub od wspólnej krawędzi - zasada symetrii ,
w przekrojach, w których naprężenie normalne osiągają ekstremum, naprężenie styczne są równe 0.
Podać zależności opisujące naprężenia w przekroju ukośnym podczas dwukierunkowego rozciągania próbki. Jakie wnioski wynikają z tych wzorów?
σσxcos2σysin2
,(σx-σy) sin2
Wnioski:
naprężenia normalne osiągają największą wartość w przekrojach k* wzajemnie prostopadłych do σx lub σy,
naprężenia styczne
Wyjaśnić pojęcia: naprężenia główne, przekroje główne, kierunki główne.
Naprężenia główne - są to naprężenia normalne σ, występujące w przekrojach głównych,
Przekroje główne - przekroje, w których naprężenia styczne nie występują,
Kierunki główne - kierunki, na których występują tylko naprężenia główne (normalne) σ Będą to, więc osie prostopadłe do przekrojów głównych.
Na wybranym przykładzie omówić metodę wykreślną znajdowania naprężeń głównych i przekrojów głównych (koło Mohra).
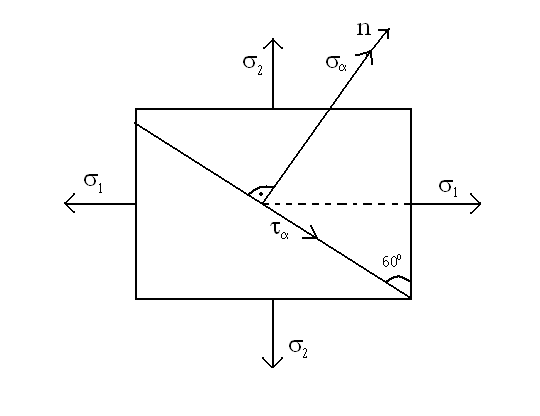
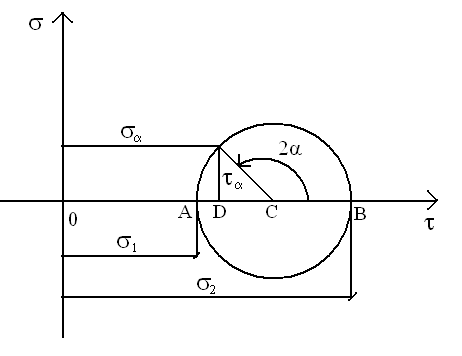
Obieramy układ odniesienia we współrzędnych σ i ,
Zakładamy określoną skalę rysunku pamiętając, aby była ona jednakowa na osi σ i ,
Nanosimy naprężenia główne σ1 i σ
Wyznaczamy środek koła Mohra na podstawie następującego wzoru:
OC=0,5(σ1+σ
Wyznaczamy promień koła Mohra:
r=0,5(σ1-σ
Rysujemy koło Mohra o promieniu r z punktu C oraz odkładamy od osi kąt 2 w kierunku
trygonometrycznym (przeciwnym do ruchu wskazówek zegara)
7. Odczytujemy wartości naprężeń stycznych i normalnych na osi σ i
Jakie warunki musi spełniać ustrój prętowy, aby stanowił kratownicę? Omów tzw. „warunek wyznaczalności kratownicy” w aspekcie jej warunku sztywności.
Aby ustrój prętowy stanowił kratownicę musi spełniać warunek sztywności, który opisuje wzór:
P = 2W - 3
P - liczba prętów
W - liczba węzłów
„Warunek wyznaczalności kratownicy” musi zostać spełniony w odniesieniu do każdej kratownicy płaskiej. Spełnienie powyższego wzoru powoduje, że kratownica jest układem statycznie wyznaczalnym i sztywnym w swej płaszczyźnie, czyli niezmienna geometrycznie. W kratownicy mogą występować pręty zerowe, to znaczy takie, które nie są ani rozciągane ani ściskane, a są jedynie wymagane do spełnienia ogólnego warunku sztywności.
Jaki układ sił otrzymujemy w węźle kratowym po uzewnętrznieniu sił w prętach? Ile równań równowagi można ułożyć dla kratownicy płaskiej?
Po uzewnętrznieniu sił w prętach otrzymujemy płaski zbieżny układ sił, dla którego możemy napisać dwa równania równowagi (sumy rzutów sił na przyjęte osie układów współrzędnych)
Na czym polega metoda równowagi węzłów (obliczania sił w prętach kratownicy)?
Metoda równoważenia węzłów polega na sprawdzeniu równowagi, czyli czy wypadkowa wszystkich sił działających w węźle równa się zero. W pierwszej kolejności wyznaczamy reakcje podporowe, a następnie wprowadzamy układ zerowy dla każdego pręta. W drugim etapie rozpatrujemy oddzielnie poszczególne węzły kratownicy z wykorzystaniem analitycznych równań równowagi. Jako kolejny i ostatnie punkt wyznaczamy, w razie potrzeby, odpowiednią średnicę pręta przy założeniu maksymalnej siły panującej w pręcie.
Na czym polega metoda Rittera (obliczania sił w prętach kratownicy)?
Metodę Rittera stosujemy wtedy, gdy chcemy wyznaczyć siłę normalną w określonym pręcie kratownicy. W tym celu przecinamy myślowo kratownicę przez pręty, wśród których jest pręt z poszukiwaną siłą normalną, a następnie rozpatrujemy równowagę odciętej części kratownicy. Ponieważ mamy do dyspozycji tylko trzy warunki równowagi, więc przeciąć kratownicę możemy tylko przez trzy pręty. Następnie zapisujemy odpowiednie równania równowagi (równania momentów względem punktów Rittera, o ile istnieją). Na koniec rozwiązujemy równania równowagi.
Co to jest środek ciężkości? Jak wyznacza się współrzędne środka ciężkości figury złożonej?
Środek ciężkości jest to środek sił równoległych w odniesieniu do sił ciężkości. Aby wyznaczyć środek ciężkości figury złożonej, obieramy układ współrzędnych, tak aby cała figura była w pierwszej ćwiartce układu. Następnie dzielimy figurę na figury proste, którą każdą rozpatrujemy oddzielnie. W kolejnym etapie obliczamy pola figur i wyznaczamy współrzędne środka ciężkości poszczególnych figur względem osi y i x. Następnie korzystając ze wzoru, obliczamy środek ciężkości całej figury względem osi y i x, otrzymując w ten sposób współrzędne środka ciężkości figury złożonej.
Gdzie leży środek ciężkości wycinka koła oraz półkola?
Środek ciężkości wycinka koła:
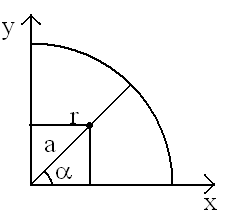
![]()
Środek ciężkości dla półkola:
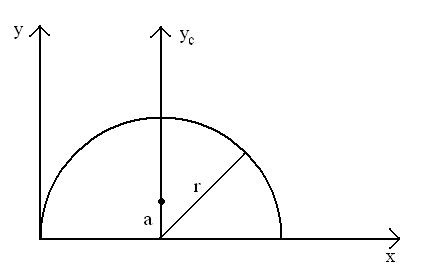
![]()
Zdefiniować moment bezwładności figury płaskiej względem osi. Podać zależności na momenty bezwładności względem osi dla kilku podstawowych figur płaskich.
Momentem bezwładności nazywamy granicę, do której dąży suma iloczynów elementarnych powierzchni przez kwadrat odległości środka tego elementu od osi, względem której obliczamy moment bezwładności.
Momenty bezwładności dla prostokąta:
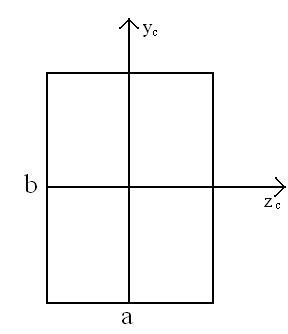
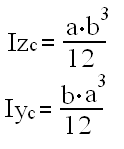
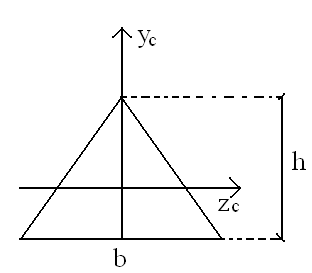
Momenty bezwładności dla trójkąta:
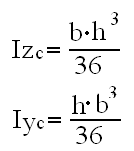
Moment bezwładności dla koła:
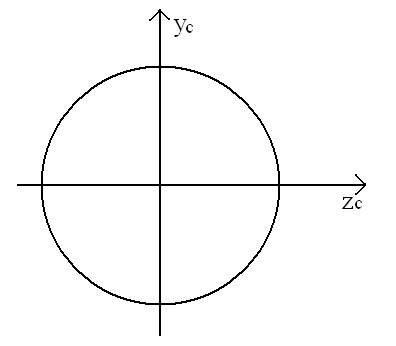
![]()
Sformułuj twierdzenie Steinera. Jaką własność mają osie centralne?
Korzystając z twierdzenia Steinera możemy obliczać momenty bezwładności względem osi przesuniętych równolegle względem siebie, z których jedna musi przechodzić przez środek ciężkości.
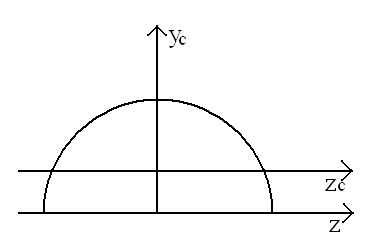
Obliczyć momenty bezwładności dla półkola względem osi centralnych z, y.
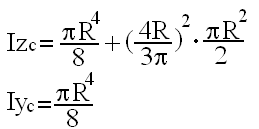
Jak można obliczyć biegunowy moment bezwładności. Podać wzór na J0 dla przekroju rurowego.
Biegunowy moment bezwładności jest sumą momentów bezwładności względem osi y i z. Można go obliczyć wykorzystując prawo Hooke'a dla czystego ścinania i wzór na moment skręcający. Wzór dla przekroju rurowego:
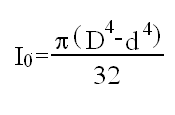
Omówić, na wybranym przykładzie, przebieg obliczeń położenia osi głównych centralnych i momentów bezwładności względem tych osi.
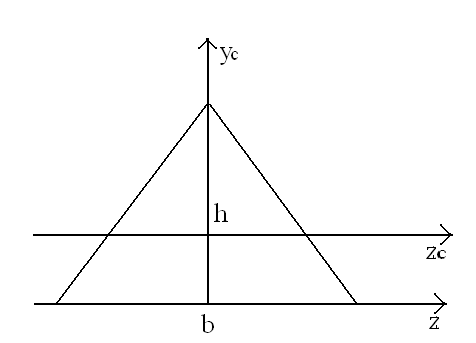
Dla trójkąta równoramiennego o wysokości h=6cm i podstawie b=4cm obliczyć:
centralne momenty bezwładności,
moment bezwładności względem podstawy,
moment bezwładności względem osi równoległej do podstawy b i przechodzącej przez wierzchołek trójkąta.
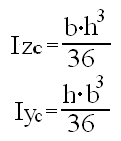
a)
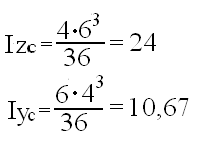
b) ![]()
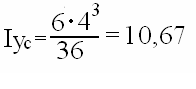
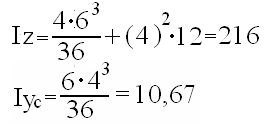
c)
Omówić ustalenia przyjmowane w teorii zginania belek. Co to jest oś obojętna przekroju belki?
Ustalenia przyjmowane w teorii zginania belek:
Przekroje poprzeczne belki, płaskie przed odkształceniem, pozostają płaskie po odkształceniu,
Włókna wzdłużne równoległe do osi belki nie wywierają na siebie nacisku i wobec tego znajdują się w jednowymiarowym stanie naprężeń, dla którego możemy przyjąć zależność między naprężeniem a odkształceniem w postaci prawa Hooke'a.
Odkształcenie włókien równoległych do osi pręta i znajdujących się w płaszczyźnie równoległej do warstwy obojętnej nie zależą od ich położenia w tej płaszczyźnie tj. ulegają tym samym wydłużeniom (skróceniom długości).
Oś obojętna przekroju jest prostą przecięcia się warstwy obojętnej z płaszczyzną pola przekroju poprzecznego belki.
Zdefiniować obciążenia wewnętrzne w belkach. Podać regułę znaków.
Do obciążeń (sił) wewnętrznych w belkach możemy zaliczy: siłę tnącą, moment zginający i siłę normalną. Siła tnąca działa prostopadle do osi belki, a więc jest styczna do przekroju poprzecznego belki. Moment zginający wywołuje zginanie belki. Siła normalne działa wzdłuż osi belki; może wywoływać jej rozciąganie (lub ściskanie). Siłę tnącą będziemy uważać za dodatnią wówczas, gdy będzie ona powodowała obrót wyciętego elementu belki w kierunku zgodnym z ruchem wskazówek zegara. W przypadku przeciwnym - siłę tnącą będziemy uważać za ujemną. Moment gnący uważać będziemy za dodatni wówczas, gdy wyginać on będzie belkę wypukłością w ujemnym kierunku osi z. W przeciwnym przypadku - moment gnący będziemy uważać za ujemny. Siłę normalną będziemy uważać za dodatnią wówczas, gdy wywołuje ona rozciąganie belki. Siły normalne wywołujące ściskanie belki uważać będziemy za ujemne.
Narysować rozkład naprężeń w belce o przekroju poprzecznym w kształcie teownika. Podać zależności matematyczne.
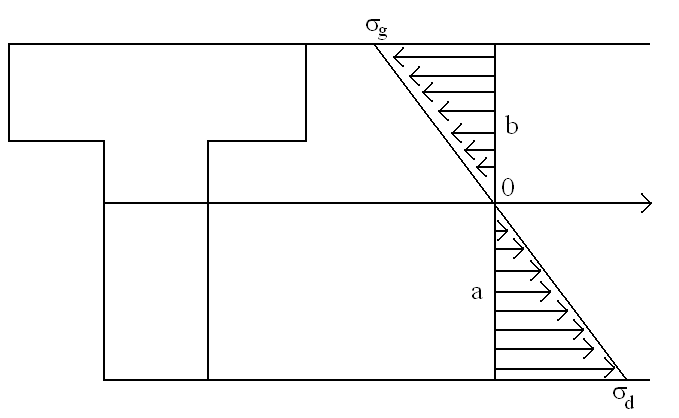
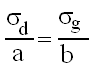
Twierdzenie Talesa
Co to jest Wz? Podać wzory dla przekrojów prostych.
Wz - wskaźnik wytrzymałości przekroju na zginanie. Jest wprost proporcjonalny do momentu bezwładności względem osi centralnej z i odwrotnie proporcjonalny do odległości najdalej wysuniętego punktu od osi obojętnej z.
![]()
Dla przekroju poprzecznego w kształcie prostokąta:
![]()
Dla przekroju poprzecznego w kształcie kwadratu:
![]()
Dla przekroju poprzecznego w kształcie koła:
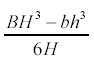
Dla przekroju poprzecznego w kształcie dwuteownika:
Napisać warunki równowagi dla wyciętego elementu belki poddanej czystemu zginaniu.
Na czym polega wymiarowanie belek?
Wymiarowanie belek polega na dobieraniu średnic z dwóch warunków: warunku wytrzymałościowego, gdzie maksymalne naprężenia styczne nie mogą przekraczać naprężeń dopuszczalnych; i warunku sztywności, który na ogół jest stały (EI), gdyż rzadko mamy do czynienia ze zmiennym przekrojem poprzecznym. Ugięcie belki o stałej wytrzymałości jest większe od ugięcia belki o stałej sztywności.
Wyjaśnić pojęcia: linia ugięcia belki, strzałka ugięcia, krzywizna belki, kąt obrotu przekroju, warunki brzegowe.
Podać równanie różniczkowe linii ugięcia belki i kątów obrotu przekrojów. Omówić interpretację stałych całkowania.
Omówić metodę Clebscha wyznaczanie linii ugięcia belek.
Omówić zależności różniczkowe między obciążeniem ciągłym, siłą tnącą i momentem gnącym w aspekcie wykresów sił wewnętrznych w belkach.
Jakie są założenia przyjmowane w teorii skręcania prętów okrągłych? Zdefiniować pojęcie momentu skręcającego.
Podać zależność pomiędzy momentem skręcającym wał M, a mocą P przenoszoną przez wał.
Na dowolnym przykładzie przedstawić sposób wykonywania wykresu kątów skręcania wału.
Na przykładzie wału o zmiennej średnicy przedstawić sposób wykonywania wykresu kątów skręcania wału.
Omówić naprężenia w przekrojach wałów skręcanych.
Omówić odkształcenia wałów skręcanych.
Wyjaśnić oznaczenia I0, W0, k , dop.
Podać W0 dla przekroju rurowego. Zapisać warunek sztywności i warunek wytrzymałościowy dla tego przekroju.
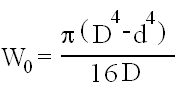
Warunek wytrzymałości dla przekroju rurowego:
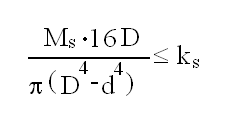
Warunek sztywności dla przekroju rurowego:
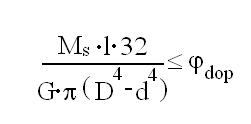
Omówić warunek wytrzymałościowy przy skręcaniu.
Warunek wytrzymałościowy dotyczy nie przekraczania naprężeń dopuszczalnych. Z tego warunku wynika, że największe naprężenie statyczne nie może przekroczyć naprężenia dopuszczalnego tzn.
![]()
We wzorze wynikającym z kryterium naprężeń dopuszczalnych średnica d występuje w 3 potędze. Stąd wniosek, że wykorzystując te kryterium możemy obliczać wały dostatecznie grube. Ponieważ „wał gruby” jest trudny do sprecyzowania, w praktyce używa się „wał krótki”
Omówić warunek sztywności przy skręcaniu.
Warunek sztywności przy skręcaniu odnosi się do nie przekraczania kątów dopuszczalnych. Aby otrzymać dostatecznie sztywną konstrukcję, należy ograniczyć jej odkształcenia sprężyste. Dla uzyskania tego warunku kąt musi być mniejszy lub co najwyżej równy pewnemu kątowi dopuszczalnemu:
![]()
We wzorze wynikającym z kryterium sztywności średnica d występuje w 4 potędze. Stąd wniosek, że warunek jest spełniony automatycznie dopiero przy dostatecznie dużej średnicy d. Dlatego, jeżeli chcemy aby kryterium sztywności było spełnione to wykorzystując warunek nie przekraczania kątów dopuszczalnych wzór ten stosujemy do obliczania wałów cienkich. Ponieważ wał cienki jest trudny do sprecyzowania w momencie, gdy nie znamy jego średnicy. Dlatego w praktyce używa się pojęcia „wał długi”.
Porównać wały pełne i drążone pod względem wytrzymałości i sztywności.
Rozpatrując rozkład naprężeń występujących w wałach pełnych, zauważamy, że naprężenia styczne rosną proporcjonalnie od wartości zerowej w osi wału do wartości maksymalnej dla ρ r. Jedynie więc skrajne (zewnętrzne) włókna są w pełni wykorzystane, natomiast materiał znajdujący się w pobliżu środka wału wykorzystany jest w niewielkim stopniu. W celu lepszego wykorzystania materiału, tj. usunięcia tej części materiału, w której naprężania są bardzo małe, zastosowano wały drążone. Wały te są lżejsze od wałów pełnych przenoszących ten sam moment skręcający Ms przy tych samych maksymalnych naprężeniach - co jest poważną zaletą dla wielu konstrukcji - a ponadto będą one sztywniejsze od wałów pełnych
Na czym polega różnica pomiędzy równowagą a statecznością?
O stateczności mówimy wtedy, gdy ciało wytrącone z położenia równowagi ciało jest w stanie samo powrócić do położenia początkowego. Natomiast o równowadze mówimy wtedy, gdy
Jak zachowują się podczas ściskania tzw. pręty smukłe?
Pręty smukłe (długie i cienkie) podczas ściskania ulegają wyboczeniu przy bardzo małych naprężeniach, czyli niewielkiej sile krytycznej Pkr. Ze wzoru Eulera wynika, że naprężenie σkr jest wprost proporcjonalne do modułu sprężystości wzdłużnej E materiału pręta, a odwrotnie proporcjonalne do kwadratu jego smukłości. W miarę wzrostu smukłości wzrasta szybko jej kwadrat, a zatem naprężenie krytyczne szybko maleje.
Narysować wykres σgr=f( i omówić zakresy stosowalności wzorów Eulera i Tetmajera.
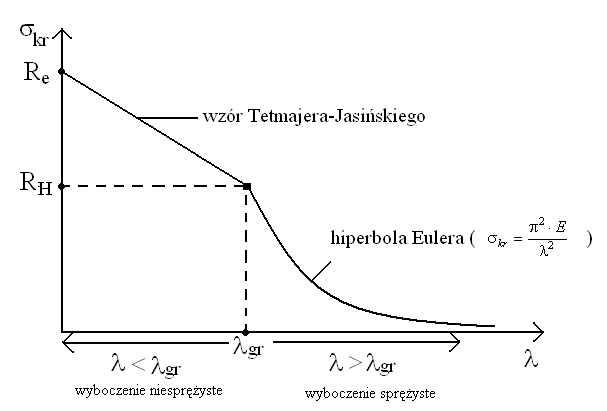
Stosowanie wzoru Eulera ogranicza się wyłącznie do smukłości większych od granicznej. Jak na wykresie widać - dla małych smukłości naprężenia krytyczne rosną bardzo szybko. Wzór Eulera jest wyprowadzany przy założeniu małej sztywności (tzn. dużej smukłości) oraz, że wyboczenie jest wyboczeniem sprężystym, to znaczy, obowiązuje prawo Hooke'a, a to oznacza dalej, że naprężenia krytyczne nie mogą przekroczyć granicy proporcjonalności.
Wzór Tetmajera-Jasińskiego odnosi się do wyboczenia niesprężystego (plastycznego). Ponieważ w konstrukcjach technicznych w celu dopełnienia warunków wytrzymałości i sztywności naprężenia dopuszczalne powinny być mniejsze od granicy proporcjonalności. Mogłoby się wydawać, że wyznaczanie naprężeń krytycznych wyższych od granicy proporcjonalności pozbawione jest większego znaczenia praktycznego. Tak jednak nie jest. Musimy bowiem pamiętać, że wyboczenie pręta stanowi dla konstrukcji większe niebezpieczeństwo niż osiągnięcie przez naprężenia granicy proporcjonalności czy nawet plastyczności.
Od czego zależy tzw. długość wyboczeniowa lw pręta?
Długość wyboczeniowa pręta zależy od sposobu zmocowania pręta i od długości pręta.
Na czym polega obliczanie nośności prętów ściskanych?
Wyjaśnić pojęcie siły krytycznej.
Siła krytyczna - to wartość siły ściskającej, po przekroczeniu, której następuje wyboczenie pręta.
Omówić wyznaczenie siły krytycznej przy wyboczeniu sprężystym.
Siłę krytyczną przy wyboczeniu sprężystym obliczamy ze wzoru Eulera:
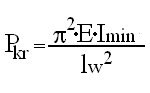
E - moduł Younga
Imin - minimalny moment bezwładności względem osi centralnej
lw2 - długość wyboczeniowa
Jednak zanim dojdziemy do tego wzoru wpierw trzeba wyliczyć:
Pole powierzchnie zadanego przekroju poprzecznego.
Momenty bezwładności względem osi centralnych y i z.
Najmniejszy promień bezwładności przekroju:
![]()
Długość wyboczeniową:
lw = l
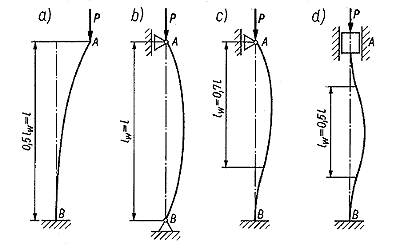
- zależna od sposobu umocowania pręta
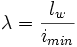
Smukłość:
Smukłość graniczną:
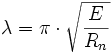
Rn - granica plastyczności
Jako ostatni punkt wyliczamy już siłę krytyczną.
Zdefiniować pojęcie smukłości gr. Podać wzór i interpretację.
Smukłość graniczna - stała materiałowa, bezwymiarowa, określająca granicę między liniowo sprężystym i sprężysto-plastycznym zakresem pracy pręta ściskanego; wartość dla stali ok.110.
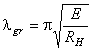
Jakie charakterystyki geometryczne przekroju decydują o smukłości pręta?
O smukłości pręta decydują długość pręta i pole przekroju poprzecznego. Pręty smukłe są długie i cienkie.
Zagadnienia cieplne:
Wyznaczanie odkształceń termicznych prętów swobodnych w polach temperatur równomiernych i nierównomiernych wzdłuż osi pręta. Średnia całkowa temperatur.
Wyznaczanie odkształceń termicznych pręta swobodnego w polu temperatur z gradientem temperatur wzdłuż wysokości pręta.
Odkształcenie układów prętowych w polu temperatur. Metoda pracy wirtualnej. Prosty przykład wyznaczania odkształcenia kratownicy.
Odkształcenia termiczne ram. Przykład.
Przyczyna powstawania naprężeń termicznych. Przykład.
Wyznaczanie sił wewnętrznych oraz naprężeń termicznych w belce statycznie niewyznaczalnej na skutek oddziaływania temperatur.
Czy wzrost temperatury może spowodować zniszczenie pręta na skutek wyboczenia.
Zjawiska reologiczne. Wpływ na nie wzrostu temperatur.
Pełzanie, od czego jest uzależnione? Czy występuje w normalnych temperaturach?
Krzywa pełzania. Okresy pełzania. Wpływ temperatury na przebieg krzywej pełzania.
Relaksacja. Wpływ temperatury na relaksacje.
Wpływ temperatury na właściwości mechaniczne stali.
Wyszukiwarka
Podobne podstrony:
ZAGADNIENIA NA EGZAMIN Z MECHANIKI TECHNICZNEJ II DLA SEMESTRU III, sem III, +Mechanika Techniczna I
ZAKRES NA EGZAMIN Z MECHANIKI TECHNICZNEJ II DLA SEMESTRU III opracowanie
Egzamin z polibudy semestr II 2
zaliczenie - pytania i odp2, Politechnika Lubelska Wydział Mechaniczny, Semestr II, Podstawy Elektro
cwiczenie 1 badanie wlasnosci mechanicznych 1, Semestr 3 moje, wytrzymałość 4sem, LABORKI, LABORKI
MECHANIKA TECHNICZNA II - ZAGADNIENIA NA EGZAMIN, +Mechanika Techniczna II - Wykład.Ćwiczenia.Labora
zag egzamin10, Rok I, semestr II, Rok II, Semestr I, Materiałoznawstwo II
Wiedza o literaturze XIX wieku- opracowane pytania egzaminacyjne, kulturoznawstwo, semestr II
egzamin0, STUDIA, SEMESTR II, Materiały Metalowe
zaliczenie - pytania i odp1, Politechnika Lubelska Wydział Mechaniczny, Semestr II, Podstawy Elektro
chemia pytania na egzamin ustny semestr II
Mechanika Semest II pytania egz
fizyka egzamin, AiR, SEMESTR II, Fizyka II
egzamin z samoobrony semestr II
Egzamin z polibudy semestr II 2
zaliczenie - pytania i odp2, Politechnika Lubelska Wydział Mechaniczny, Semestr II, Podstawy Elektro
Egzamin z Wytrzymałości Materiałów II - Zagadnienia 2012, PWr Mechaniczny [MBM], Semestr 4, Wytrzyma
wydymala-egzamin, Wytrzymałość materiałów sciąga, WYTRZYMAŁOŚĆ MATERIAŁÓW (semestr II)
więcej podobnych podstron