ĆWICZENIA LABORATORYJNE Z FIZYKI
S P R A W O Z D A N I E
Temat: Pomiar wilgotności powietrza za pomocą psychrometru.
Wyznaczanie stosunku ciepła właściwego gazu przy stałym ciśnieniu do molowego ciepła właściwego przy stałej objętości (Cp / Cv).
Natalia Obrębska
Michał Nadrajkowski
para nr 11, ćwiczenie nr 18/27
Technologia żywności i żywienie człowieka
Grupa 8
Zagadnienia Teoretyczne:
Wilgotnością bezwzględną powietrza nazywamy masę pary wodnej zawartej w 1 m3 powietrza. Jej wymiarem jest ![]()
. Wilgotnością względną powietrza nazywamy stosunek masy pary wodnej m1 zawartej w pewnej objętości powietrza do tej masy pary wodnej m2, którą miałaby para wodna nasycona w tej objętości powietrza, w danej temperaturze:
![]()
Masa pary m w danej objętości zależy od gęstości ρ(m = ρυ), a gęstość jest wprost proporcjonalna do ciśnienia p, możemy więc napisać: m = a , gdzie a - współczynnik proporcjonalności, oraz
![]()
![]()
gdzie: p1 - prężność pary wodnej zawartej w powietrzu w pewnej temperaturze, p2 - prężność pary wodnej nasyconej w tej temperaturze.
Wilgotność względną wyrażamy zwykle w %.
![]()
Ciepło. Pierwsza zasada termodynamiki w swej najprostszej (szczególnej) postaci ma zapis:
![]()
gdzie:
ΔU - zmiana energii wewnętrznej
W - praca
Q - ciepło
Zmianę energii wewnętrznej ΔU układu można osiągnąć dwoma sposobami:
a) za pośrednictwem pracy,
b) za pośrednictwem ciepła.
Załóżmy, że praca i ciepło są dodatnie, czyli wzbogacają układ w energię, tzn. że ΔU>0, co najczęściej objawia się wzrostem temperatury lub zmianą fazy układu. Układ zyskał energię, jednak praca nie jest energią. Idąc zatem śladami matematycznego porządku, musimy stwierdzić, że drugi składnik sumy w równaniu ![]()
, czyli Q, musi być składnikiem tego samego rodzaju co W, a więc też nie jest energią. Stwierdzamy zatem, że praca i ciepło są jedynie sposobami - formami przekazywania energii. Obie formy mają swoją miarę, a obie miary wspólną jednostkę - dżul. Energia przenoszona obydwoma sposobami jest mierzalna, np. termoergometrem oraz kalorymetrycznie.
Ilość energii przekazanej za pośrednictwem pracy powinniśmy nazywać nie pracą, lecz energetyczną równowartością pracy, a ilość energii przekazanej za pośrednictwem ciepła powinniśmy nazywać nie ciepłem, lecz ilością ciepła. Wartość zmiany energii wewnętrznej oznaczamy przez ΔU. Dżul jest jednostką nie samych form, lecz odpowiednich wartości przekazywanej energii. Od dziesiątków lat przywykliśmy ilość ciepła nazywać po prostu ciepłem, toteż nawyku tego nie będziemy uważali za błędny, pod warunkiem jednak, że potrafimy oba pojęcia odróżnić. Przekazywanie energii w formie ciepła wiąże się z różnicą temperatur między dwoma układami lub między dwoma miejscami tego samego układu. Przez ciepło będziemy rozumieli ilość ciepła, a to oznacza ilość (wartość) energii przepływającej w wyniku istnienia różnicy temperatur. W tym sensie ciepło bywa też nazywane energią cieplną lub termiczną. Z zasadniczych względów lepiej tych określeń unikać.
Temperatura. Mechaniczne oddziaływanie dwóch ciał na siebie umownie nazwano siłą. Jeśli to oddziaływanie jest duże mówimy, że siła ma dużą wartość. Miarą oddziaływania, czyli siły, są skutki tego oddziaływania (statyczne lub dynamiczne). Podobną umową jest temperatura. Pojęcie temperatury wprowadzono w celu określenia stanu chaotycznego ruchu cząsteczek danego ciała, a dokładnie - w celu określenia energii kinetycznej związanej z chaotycznym ruchem cząsteczek. Temperatura nie określa wartości energii ruchu cząsteczek, ale jest wielkością, która do tej energii jest wprost proporcjonalna. Jej jednostką nie jest dżul, ale kelwin (K) lub stopień Celsjusza (˚C).
Wzór na energię kinetyczną cząsteczek można zapisać następująco:
![]()
Jest to wzór Boltzmana dla gazu doskonałego, którego wyprowadzenie łatwo znaleźć w podręcznikach fizyki, gdzie:
![]()
- średnia energia kinetyczna cząsteczek danego układu, przeliczona na jedną cząsteczkę tego układu,
k - stała Boltzmana,
![]()
R - stała gazowa,
N - liczba Avogadra,
T - temp. mierzona w skali bezwzględnej (Kelwina)
Przedstawiony zapis jest wprawdzie praktyczny, gdyż łatwiej jest mierzyć temperaturę niż wartość energii ruchu cząsteczek ciała, w rzeczywistości jednak to nie energia zależy od temperatury, lecz odwrotnie - temperatura jest funkcją energii. Wzrost temperatury ma związek ze wzrostem energii lub wzrost temperatury oznacza wzrost energii.
Energia kinetyczna całego układu jest sumą energii kinetycznych wszystkich cząsteczek tego układu. Średnia energia kinetyczna każdej cząsteczki danego układu w stanie stacjonarnym jest taka sama, dlatego suma tych energii może być podana jako krotność wyrażenia ![]()
![]()
gdzie:
n - liczba cząsteczek
Dla dowolnej liczby stopni swobody (i) piszemy:
![]()
stąd ![]()
T nie zależy od n, gdyż E jest wprost proporcjonalna do n, czyli w danych warunkach:
![]()
Energia wewnętrzna i ilość ciepła. Przez energię wewnętrzną układu rozumiemy sumę wszystkich rodzajów energii zawartych w układzie. Są to energie wewnątrzatomowe i wewnątrzcząsteczkowe, energie potencjalne wynikające z oddziaływań międzycząsteczkowych oraz energie kinetyczne ruchu postępowego, drgającego i obrotowego cząsteczek. Temperatura wiąże się tylko z energią kinetyczną.
Przez „ilość ciepła” lub „ciepło” rozumiemy tę część energii wewnętrznej, która jest przekazywana (mówimy „przepływa”) między dwoma ciałami lub dwoma miejscami tego samego ciała, między którymi istnieje różnica temperatur. Zgodnie z określeniem temperatury przekazywana jest w ten sposób energia kinetyczna.
Parametry termodynamiczne określające stan gazu to: ciśnienie p, temperatura T w skali bezwzględnej i objętość V. Dla gazu doskonałego, którego cząsteczki mają trzy stopnie swobody, ciśnienie p wyraża się wzorem:
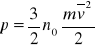
gdzie:
n0 - liczba cząsteczek gazu w jednostce objętości,
m - masa jednej cząsteczki,
v - średnia prędkość cząsteczek.
Wzór ten nazywa się podstawowym równaniem teorii kinetyczno-molekularnej.
Równaniem stanu gazu doskonałego jest równanie Clapeyrona, które wyraża związek między trzema parametrami stanu gazu (p, V, T).
![]()
gdzie:
Vμ - obj. jednego mola gazu,
R - stała gazowa ![]()
,
T - temperatura w skali bezwzględnej.
Procesy adiabatyczne. Procesy adiabatyczne są to takie przemiany gazowe, które zachodzą bez wymiany ciepła z otoczeniem. Pierwsza zasada termodynamiki przyjmuje postać:
![]()
gdzie:
ΔU - wzrost lub ubytek energii wewnętrznej, zależnie od znaku W.
Energia wewnętrzna 1 mola gazu doskonałego jako funkcja temperatury ma następującą postać:
![]()
gdzie:
Cv - molowe ciepło właściwe gazu przy stałej objętości.
Przyrost energii wewnętrznej na skutek zmiany temperatury oblicza się przez zróżniczkowanie względem temperatury wyrażenia
![]()
Praca, jaką wykonuje gaz przy adiabatycznym zwiększeniu objętości o dowolnie małą wartość dV, równa się:
![]()
Biorąc powyższe pod uwagę, dla dowolnie małych zmian energii wewnętrznej dU, I zasadę termodynamiki dla procesów adiabatycznych można zapisać w postaci:
![]()
Wartość ciśnienia, jakie wywiera gaz na ścianki naczynia, wynika z równania Clapeyrona
![]()
Przekształcając, otrzymamy:
![]()
Całkując powyższe równanie w granicach zmian objętości i temperatury
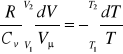
otrzymuje się równanie Poissona:
![]()
lub ![]()
gdzie: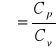
Cp - molowe ciepło właściwe przy stałym ciśnieniu gazu.
Ćwiczenie 18.
Pomiar wilgotności powietrza za pomocą psychrometru.
Obliczenia i pomiary:
Pomiar nr |
t1 [K] |
t2 [N/m2] |
p2 [N/m2] |
p [N/m2] |
p1 [N/m2] |
b [N/m2] |
W [%] |
||||
1 |
295,45 |
288,15 |
2691,327 |
1704,907 |
1370,086 |
99708,48 |
50,91 |
||||
2 |
296,15 |
288,45 |
2725,3185 |
1739,565 |
1386,398 |
99708,48 |
50,87 |
||||
3 |
296,35 |
289,15 |
2838,29 |
1816,879 |
1486,645 |
99708,48 |
52,38 |
||||
4 |
296,75 |
289,95 |
2917,937 |
1916,854 |
1604,966 |
99708,48 |
55 |
||||
Prężność pary wodnej p1: p1 = p - k (t1 - t2) b
Wilgotność powietrza: ![]()
k = 0,0046
Pomiar 1.
t1= 295,45 K p2 = 2691,327 Pa
t2= 288,15 K p = 1704,907 Pa
b=99708,48
![]()
= ![]()
![]()
![]()
= ![]()
Pomiar 2.
t1= 296,15 K p2 = 2725,3185 Pa
t2= 288,45 K p = 1739,565 Pa
b=99708,48
![]()
![]()
![]()
= ![]()
Pomiar 3.
t1= 296,35 K p2 = 2838,29 Pa
t2= 289,15 K p = 1816,879 Pa
b=99708,48
![]()
=![]()
![]()
=![]()
Pomiar 4.
t1= 296,75 K p2 = 2917,937 Pa
t2= 289,95 K p = 1916,854 Pa
b=99708,48
![]()
= ![]()
![]()
=![]()
Ocena niepewności wyniku pomiaru:
![]()
![]()
![]()
Dla wielkości t1 niepewność standardowa wyznaczona z wielkości działek z przyrządu:
Δt1= 0,2K
Dla wielkości t2 niepewność standardowa wyznaczona z wielkości działek z przyrządu:
Δt2= 0,2K
Dla wielkości b niepewność standardowa wynosi:
Δb=133,3 Pa
Dla wielkości p :
t = 288,15 p = 1704,907 Pa
Δt= 0,2K
t1 = 288,15 + 0,2 K = 288,35 K p = 1730,234
t2 = 288,15 - 0,2 K = 287,95 K p =1679,580
Δp=![]()
Dla wielkości p2:
t = 295,45 K p2 = 2691,327 Pa
Δt= 0,2K
t1 = 295,45+0,2K = 295,65K p=2725,3185
t2 = 295,45-0,2K =295,25K p=2660,0015
Δp2=![]()
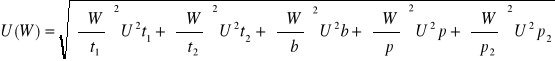
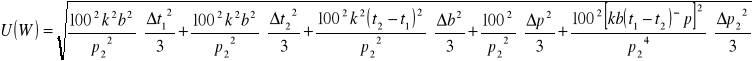
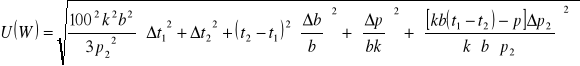
Δt1=Δt2=Δt3
![]()
![]()
W=50,91(0,71)%
Ćwiczenie 27.
Wyznaczanie stosunku ciepła właściwego gazu przy stałym ciśnieniu do molowego ciepła właściwego przy stałej objętości (Cp / Cv).
Obliczenia i pomiary:
Nr pomiaru |
t [˚C] |
h1 [mm] |
h2 [mm] |
h1 - h2 [mm] |
|
I |
23 |
498 |
167 |
331 |
1,5045 |
II |
23 |
525 |
279 |
246 |
2,1341 |
III |
23 |
518 |
124 |
394 |
1,3147 |
IV |
23 |
540 |
83 |
457 |
1,1816 |
V |
23 |
191 |
55 |
136 |
1,4044 |
VI |
23 |
500 |
121 |
379 |
1,3192 |
VII |
23 |
550 |
131 |
428 |
1,3060 |
VIII |
23 |
539 |
133 |
406 |
1,3275 |
IX |
23 |
557 |
138 |
419 |
1,3293 |
X |
23 |
578 |
140 |
438 |
1,3196 |
średnia: 1,4141 |
|||||
![]()
Ocena niepewności wyniku pomiaru:
Do tego oznaczenia możemy zastosować metodę typu A.
Pomiar przeprowadzamy 10 razy: n=10
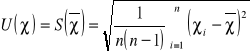
Nr pomiaru |
|
|
|
|
I |
1,5045 |
1,4141 |
0,0904 |
8,172 10-3 |
II |
2,1341 |
1,4141 |
0,72 |
5,172 10-1 |
III |
1,3147 |
1,4141 |
-0,0994 |
9,880 10-3 |
IV |
1,1816 |
1,4141 |
-0,2325 |
5,406 10-2 |
V |
14044 |
1,4141 |
-0,0097 |
9,409 10-5 |
VI |
1,3192 |
1,4141 |
-0,0949 |
9,006 10-3 |
VII |
1,3060 |
1,4141 |
-0,1081 |
1,168 10-2 |
VIII |
1,3275 |
1,4141 |
-0,0866 |
7,499 10-3 |
IX |
1,3293 |
1,4141 |
-0,0848 |
7,191 10-3 |
X |
1,3196 |
1,4141 |
-0,0945 |
8,930 10-3 |
0,063491 |
![]()
![]()
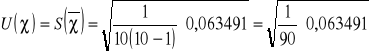
![]()
=0,027
![]()
Obliczamy teraz niepewność pojedynczego pomiaru (Pomiar 1.) Stosujemy metodę typu B/
Określamy szerokości połówkowe:
Δh1 = 2mm
Δh2 = 2mm
Δh1=Δh2= Δh=2 mm
![]()
![]()
Założoną niepewność standardową pomiaru 1 wyliczamy ze wzoru:
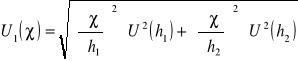
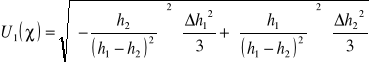
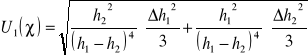
Δh1=Δh2= Δh
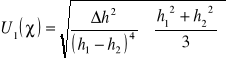
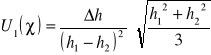
![]()
Δh= 2mm
h1 = 498 mm
h2 = 167 mm
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
10, Wyznaczanie wilgotności powietrza za pomocą psychrometru Assmanna, NAZWISKO: NAJUCH
Pomiar małych rezystancji za pomocą mostka sześcioramiennego sprawozdnie psk Tabele i wykresy(do d
fizyka sprawozdania, Pomiar długości fali świetlnej za pomocą siatki dyfrakcyjne, Sprawozdanie z ćwi
fizyka sprawozdania, Pomiar długości fali świetlnej za pomocą siatki dyfrakcyjne, Sprawozdanie z ćwi
Wyznaczanie momentu bezwładności brył za pomocą drgań skrę(1 (2), Sprawozdania - Fizyka
Wyznaczanie gęstości za pomocą piometru, STUDIA, sprawozdania, Fizyka
cw 10 - Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego, Sprawozdania jakieś, F
cw 14 - Wyznaczanie napięcia powierzchniowego cieczy za pomocą wagi torsyjnej, Sprawozdania jakieś,
cw 15 - Wyznaczanie współczynnika lepkości cieczy za pomocą wiskozymetru Stockes’a, Sprawozdania j
Cw 05 - Wyznaczanie przyspieszenia grawitacyjnego g za pomocą wahadła balistycznego, Sprawozdania fi
Wyznaczanie momentu bezwładności brył za pomocą drgań skrę(2, Sprawozdania - Fizyka
Sprawozdanie 208 - Wyznaczanie pętli histerezy ferromagnetyków za pomocą halotronu, Fizyka
56-57 1, PWR ENERGETYKA sem II, FIZYKA 2 LABORKI, LABORKI NUMERAMI, fizyka-lab, 56 &57. POMIAR INDUK
POMIAR INDUKCJI MAGNETYCZNEJ ZA POMOCĄ EFEKTU HALLA, Matematyka - Fizyka, Pracownia fizyczna, Badani
Pomiar indukcji magnetycznej za pomocą fluksometru, Szkoła, penek, Przedmioty, Fizyka, Laborki
Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła rewe, Sprawozdania - Fizyka
POMIAR INDUKCJI MAGNETYCZNEJ ZA POMOCĄ FLUKSOMETRU. BADANIE EFEKTU HALLA, Matematyka - Fizyka, Praco
Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła rewe (2), Sprawozdania - Fizyka
więcej podobnych podstron