Doświadczalnictwo zootechniczne - ćwiczenia!!!

Estymacja punktowa.

Pobierając próbę możemy ją opisać za pomocą tzw statystyk (charakterystyk). Sposób wyznaczania tych statystyk zależy od tego jak zebrane są dane. Dane mogą być zebrane albo w szereg statystyczny albo w szereg rozdzielczy, w tym rozdzielczy z przedziałami klasowymi.

Szereg statystyczny jest wtedy gdy dane są „napisane ciurkiem” i może on być uporządkowany bądź nieuporządkowany. Dane zebrane w szereg rozdzielczy są wtedy gdy występuje wartość cechy i częstość jej występowania.

Z szeregiem rozdzielczym mamy doczynienia wtedy gdy cechy zebrane są w przedziały.

Wyznaczanie miar statystycznych.

Podstawowe miary statystyczne z podkreśleniem

Zadanie 1

Dane są przyrosty dzienne 10 tuczników w kg:

xi : 0,57 0,78 0,64 0,73 0,78 0,64 0,76 0,57 0,65 0,64

i = 1, 2 ... 10 = n

n - liczba danych wyników w szeregu.

Obliczyć charakterystyki na podstawie szeregu statystycznego i szeregu rozdzielczego.

0,57 0,57 0,64 0,64 0,64 0,65 0,73 0,76 0,78 0,78

Miary skupienia:

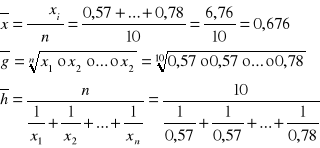
Zalezność pomiędzy średnimi:

Mediana jest to wartość która leży w środku szeregu statystycznym uporządkowanego,

n - parzyste to stosujemy wzór:

n - nieparzyste

Medianą jest wartość x piątego z kolei

Me = 0,64 v Me = 0,65

Moda - wartośc która w szeregu występuje najczęściej. Mo = 0,64

Miary rozproszenia:

Odchylenie od średniej:

0,57 - 0,676 = - 0,106

0,57 - 0,676 = - 0,106

.

.

0,78 - 0,676 = - 0,104

suma = 0

odchylenie przeciętne - d:

Wariancja:

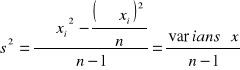
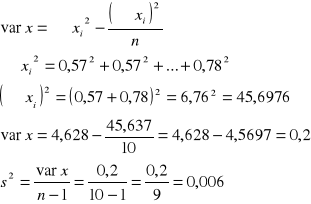
Odchylenie standardowe - s:

Współczynnik zmienności:

Rozstęp:

Ćwiczenia 2

Wyznaczanie miar statystycznych dla szeregu rozdzielczego.

Zadanie 2.

Wyznaczyć miary statystyczne dla szeregu rozdzielczego utworzonego z danych z poprzedniego zadania.

Szereg rozdzielczy to taki szereg w którym występuje wartość x i częstośc jego występowania.

X_i n_i x_i*n_i x_i²* n_i

0,57 2 1,14 0,572 * 2 = 0,64

0,64 3

0,65 1

0,73 1

0,76 1

0,78 2

En_i = 10 E = 6,76 E = 4,628

W szeregu rozdzielczym tak samo jak w szeregu statystycznym wylicza się medianę, modę, odchylenie standardowe, współczynnik zmienności i rozstęp, różnice występują w obliczaniu średniej arytmetycznej i wariancji.

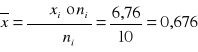
Mediana:

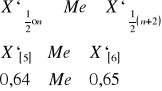
Moda:

Mo = 0,64

Wariancja:

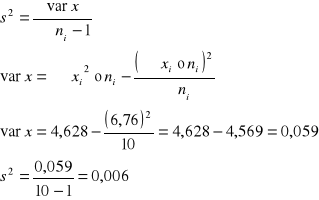
Odchylenie standardowe:

współczynnik zmienności:

Rozstęp:

Budowanie przedziałów ufności - estymacja przedziałowa.

Populacje charakteryzują parametry np. m - średnia populacji. δ - odchylenie standardowe populacji. Parametrów populacji nie znamy i szacujemy je na podstawie próby przyjmując np. δ = s.

Parametry szacujemy metodami: (Egzam)

1. MNK - metoda najmniejszych kwadratów,

2. NW - największej wiarygodności.

Estymacja przedziałowa polega na obudowaniu parametru przedziałem ze z góry określonym prawdopodobieństwem popełnienia błędu α.

α - poziom istotności - jest to % błędu jaki możemy popełnić.

W naukach przyrodniczych α = 0,05 (5%) lub α = 0,01 (1%)

1-α - jest to tzw współczynnik ufności jest to prawdopodobieństwo słuszności wniosku 1-α = 0,95 lub 1 - α = 0,99

Przedział ufności dla średniej populacji.

t _{α, V} - odczyt z tablic testu t-studenta

α = 0,05 lub α = 0,01

V = n - 1

V - stopnie swobody

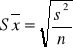
błąd średniej arytmetycznej

Zadanie

Zbudować przedział ufności dla średnich przyrostów tuczników na podstawie danych z poprzedniego zadania przyjmując:

1. α = 0,05

2. α = 0,01

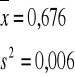
a)

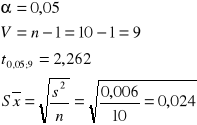
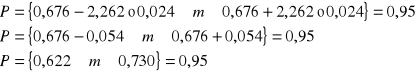
Z prawdopodobieństwem 95% stwierdzamy że prawdziwa średnia badanej populacji jest wartością z przedziału od 0,622 do 0,730. Średnie dzienne przyrosty tuczników w skali populacji sa wartoscią z przedziału 0,622 do 0,730

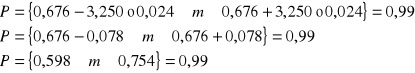
z prawdopodobieństwem 99 % stwierdzamy że.....

Przedział ufności dla różnicy średniej dwóch populacji.

x₁, x₂ - średnie arytmetyczne z prób

t _{L, V} -

V = n₁ + n₂ - 2 - stopnie swobody

Sr - błąd różnicy średnich

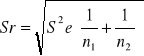
S²e - wariancja błędu

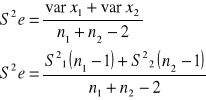
Zadanie 6.

Dane są dzienne przyrosty tuczników uzyskane po zastosowaniu dwóch rodzajów paszy.

Próba 1 - pasza 1

Próba 1 Próba 2

0,57 0,48

0,57 0,49

0,64 0,51

0,64 0,51

0,64 0,52

0,65 0,53

0,73 0,53

0,76 0,62

0,78 0,62

0,78 0,62

0,63

3,373

Zbudować przedział ufności dla różnicy średnich przyrostów, przyjmując α=0,05

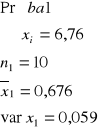
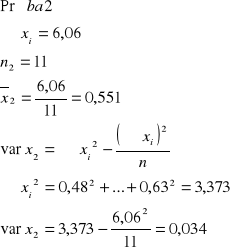
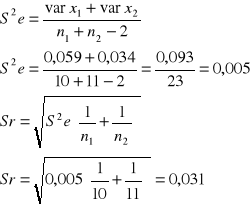
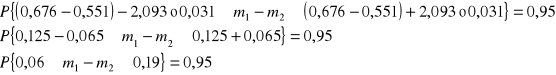
Stwierdzamy że różnica w średnich przyrostach tuczników żywionych dwoma paszami waha się od 0,06 do 0,19 kg

Weryfikacja hipotez.

Hipotezy weryfikujemy przy pomocy:

1. Przedziałów ufności.

2. Przy pomocy testu t-studenta.

Weryfikacja hipotez o średniej populacji. Hipoteza ta dotyczy takiego przypadku gdy zakładamy że średnia populacji przyjmie konkretną wartość.

Weryfikacja hipotezy przy pomocy przedziału ufności:

1.

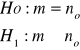
Hipoteza alternatywna (H₁) jest przeciwstawną hipotezie zerowej w takim sensie jeżeli odrzucamy hipotezę zerową to przyjmujemy alternatywną.

2.

3. Wnioskowanie:

Jeżeli wartość hipotetyczna m_o mieści się w określonym przedziale hipotezę zerową przyjmujemy, jeżeli się nie mieści hipotezę zerową odrzucamy.

Weryfikacja hipotez przy pomocy testu t-studenta.

1.

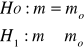
2.

3.

Wnioskujemy:

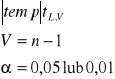
Wartość testu temp - odczytujemy z tablic

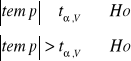
Zadanie 7.

Na podstawie danych z zadania poprzedniego hipotezę, że średnie przyrosty tuczników wynoszą 0,75 kg przyjmując oba poziomy ufności:

1. przy pomocy przedziału ufności,

2. przy pomocy testu t-studenta

a)

1.

n_o=0,75 kg

2.

3.

Z prawdopodobieństwem 95 % hipotezę 0 odrzucamy i stwierdzamy że średnie przyrosty tuczników są różne niż 0,75 kg. Z prawdopodobieństwem 99% hipotezę zerową przyjmujemy i stwierdzamy że średnie przyrosty są równe 0,75kg.

b)

1.

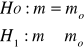
2.

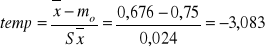
3.

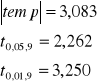
Z prawdopodobieństwem 95 % hipotezę przyjmujemy a z prawdopodobieństwem 99% hipotezę odrzucamy.

Weryfikacja hipotez o różnicy średnich dwóch populacji.

Hipoteza ta zakłada że dwie populacje n₁ i n₂ są sobie równe.

Przy pomocy przedziału.

1.

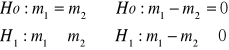
2.

3.

Jeżeli 0 mieści się w określonym przedziale hipotezę zerową przyjmujemy, jeżeli się nie mieści hipotezę zerową odrzucamy.

Przy pomocy testu t-studenta.

1.

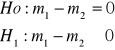
2.

3.

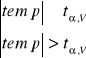
V= n₁ + n₂ - 2

Zadanie.

Na podstawie danych z zadania poprzedniego zweryfikować hipotezę, że przyrosty tuczników nie zależą od zastosowanej paszy (rodzaj paszy nie wpływa na przyrosty wagowe) przyjmując L=0,05:

1. przy pomocy przedziału,

2. testu t-studenta

1.

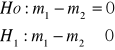
2.

3.

Hipotezę zerową odrzucamy i stwierdzamy, że istnieją różnice w przyrostach tuczników w zalezności od rodzaju paszy.

b) t-studenta

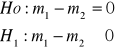
2.

3.

t_{0,05; 19} = 2,093 V = 11 + 10 - 2 = 19

Hipotezę zerową odrzucamy.

Analiza wyników doświadczenia jednoczynnikowego założonego w układzie wielogrupowym prostym z jednakową liczbą obserwacji w podklasie.

Model liniowy.

1.

2. Hipotezy zerowe:

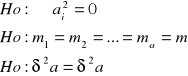
δ²a - wariancja w populacji.

3.

W doświadczeniu badano wpływ długości odchowu gęsi na ich końcową mas ciała (kg):

	A1	A2	A3	A4
	3,2	3,8	4,2	4,5
		3,4	4,1	4,3	4,5
		3,5	4,4	5,0	5,6
		4,1	4,3	5,4	6,2
		4,0	4,3	5,5	6,1
Yi.	18,2	20,9	24,4	26,9
	3,64	4,18	4,88	5,38

Analiza wyników doświadczenia 2 czynnikowego w klasyfikacji krzyżowej z 1 obserwacją w podklasie.

1. Model liniowy.

2.

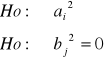
3.

Badano współczynnik strawności białka surowego owsa w żywieniu gęsi z uwzględnieniem systemu utrzymania (a₁ - system tradycyjny, a₂ - system intensywny) oraz dawki owsa (50,100,150,200 g).

	B1	B2	B3	B4	Yi.
A1	61,2	65,3	64,8	65,2	256,5
A2	63,2	63,4	61,3	60,2	248,1
Y.j	124,4	128,7	126,1	125,4	504,6

4.

a=2 b = 4 N = ab = 8

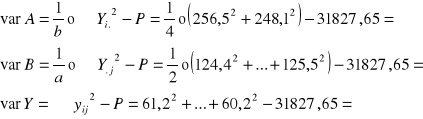
Źródła zmienności	Sumy kwadratów	Stopnie swobody	Wariancja:	Femp	Ftab
System utrzymania	8,82	a-1 2 - 1 = 1	8,82	1,94	10,13	34,12
Dawka owsa	5,06	b -1 4 - 1 = 3	1,69	<1
Błąd	13,61	3	4,54
Całość:	27,49	N - 1 = 7

Ani system utrzymania ani dawka owsa nie miały istotnego wpływu na współczynnik strawności.

Analiza wyników doświadczenia dwuczynnikowego w klasyfikacji krzyżowej z więcej niż jedną obserwacją w podklasie.

1. Model liniowy:

ab_ij - efekt interakcji czynników a i b. Interakcja współdziałanie - są to różnice w działaniu 1 czynnika na tle różnych poziomów drugiego czynnika.

2. Hipotezy zerowe:

3.

Badano wpływ płci i dawki paszy (50, 100, 150 g) na przyrosty wagowe kacząt.

4.

a = 2

	B1	B2	B3	Yi..
A1	1,5	1,9	3,3
	2,0	1,9	2,9
	1,0	2,1	2,4
	1,1	1,3	2,5
Yij.	5,6	7,2	11,1	23,9
A2	1,2	1,9	2,4
	1,3	2,1	2,2
	1,0	2,4	2,2
	1,1	2,2	1,9
Yij.	4,6	8,6	8,7	21,9
Y.j.	10,2	15,8	19,8	45,8

Tabela AxB

	B1	B2	B3	Yi..
A1	5,6	7,2	11,1	23,9
A2	4,6	8,6	8,7	21,9
Y.j.

a = 2 b = 3 n = 4 N = abn N=24

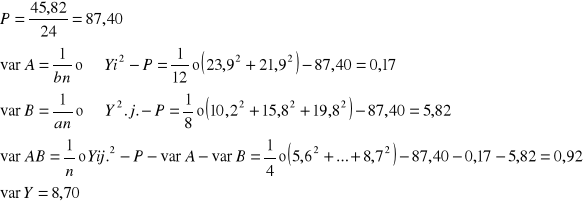
Źródła zmienności	Suma kwadr.	Stopnie swobody:	Wariancja:	Femp:	Ftab
										0,05	0,01
Płeć (cz A)	0,17	a - 1 2 - 1=2			4,41	8,25
Pasza (cz B)	5,82	b - 1 3-1 = 2	2,91	29,39**	3,55	6,01
Interakcja AxB Płeć x Pasza	0,92	(a-1)(b-1) 2	0,46	4,65	3,55	6,01
Błąd:	1,79	ab(n-1) 18	0,099
Całość:	8,70	N-1 = 23

Wniosek:

Dawka paszy (czynnik B) miała wysoce istotny wpływ na przyrosty wagowe kacząt. Płeć (czynnik A) nie miała istotnego wpływu na przyrosty wagowe kacząt.

Szczegółowe porównanie średnich

Dla dawek paszy - czynnik B

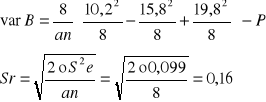
T_{0,05; 3; 18} = 2,55 NIR_0,05 = 0,16 * 2,55 = 0,41

T_{0,01; 3; 18} = 3,32 NIR_0,01 = 0,16 * 3,32 = 0,53

	1,28	1,98	2,48
1,28		0,70**	1,20**
1,98			0,50*
2,48

Średnia pierwsza różni się (jest mniejsza) wysoce istotnie od pozostałych dwóch średnich. Średnia druga różni się (jest mniejsza) istotnie od średniej trzeciej.

Dla interakcji AxB

Płeć jest czynnikiem jakościowym a dawka paszy jest czynnikiem ilościowym. Podstawowym kierunkiem badania interakcji jest badanie poziomu czynnika ilościowego na tle poziomu jakościowego (dawek paszy na tle płci).

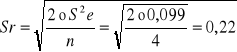
Odczyt z tablic Tukey`a ten sam co wyżej.

NIR_0,05=0,22 * 2,55 = 0,561

	B1	B2	B3
A1		1,8	2,78
A2	1,15	2,15	2,17

Dla płci A1:

	1,4	1,8	2,78
1,4	///	0,4	1,38*
1,8		///	0,98*
2,78			///

Dla płci A2

	1,15	2,15	2,18
1,15	///	1*	1,03*
2,15		////	0,03
2,18			////

1

Miary statystyczne (szereg statystyczny, charakterystyki).

Miary skupienia:

• średnia arytmetyczna -
  

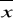
• średnia geometryczna -
  

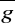
• średnia harmoniczna -
  

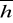
• mediana - Me,

• Moda - Mo

średnie

Miary rozproszenia:

• odchylenie od średniej
  

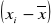
• odchylenie przeciętne - d

• wariancja - s²

• odchylenie standardowe - s

• współczynnik zmienności - V

• rozstęp - R

przyjmujemy

odrzucamy

Ho przyjmujemy

Ho odrzucamy

---