O2 -Wyznaczanie ogniskowych soczewek i badanie wad soczewek

1. Wstęp teoretyczny

• Światło i zjawiska związane z jego rozchodzeniem się

Światło wykazuje naturę korpuskularno - falową. Według teorii korpuskularnej światło jest zbiorem cząstek pozbawionych masy, o skwantowanej energii. Rozpatrując zjawiska związane z rozchodzeniem się światła, wygodniej jest jednak posługiwać się teorią falową. Zgodnie z nią światło to fala elektromagnetyczna, a więc z jej rozchodzeniem się związane są takie zjawiska jak: odbicie, załamanie i dyspersja.

Odbicie pojawia się na granicy dwóch ośrodków i polega na nagłej zmianie kierunku rozprzestrzeniania się promieni świetlnych. Zjawisko odbicia podlega prawu odbicia, zgodnie z którym kąt padania jest równy kątowi odbicia, a promień padający i odbity oraz normalna leżą w jednej płaszczyźnie. Oczywiście w efekcie odbicia fala pozostaje w ośrodku, w którym się rozchodziła, a jej długość nie ulega zmianie.

Załamanie światła również pojawia się na granicy dwóch ośrodków i podobnie jak odbicie polega na zmianie kierunku rozchodzenia się promieni świetlnych. Jednak w przypadku załamania fala „przechodzi” do drugiego ośrodka. Ponadto jej długość ulega zmianie. Stosunek prędkości fal w poszczególnych ośrodkach jest równy stosunkowi współczynników załamania światła w tych ośrodkach oraz stosunkowi sinusów kąta padania i kata załamania. Zależność ta określana jest jako prawo załamania (prawo Snella).

Dyspersja to zależność prędkości fazowej fali od jej długości. Efektem tej zależności jest rozszczepienie światła (gdyż światło o różnych długościach fali załamuje się pod różnymi katami).

• Soczewki

Soczewka to urządzenie optyczne wykonane z przeźroczystego materiału, ograniczone dwoma powierzchniami sferycznymi, których środki leżą na osi optycznej soczewki. Soczewki wykorzystują zjawisko załamania światła na granicy dwóch ośrodków do tworzenia obrazów (rzeczywistych lub pozornych). Możemy je podzielić na skupiające („skupiają” promienie) i rozpraszające („rozpraszają” promienie). Soczewkę charakteryzuje wielkość zwana ogniskową. Ogniskowa to odległość ogniska F od płaszczyzny środkowej soczewki. Ognisko F jest to miejsce, w którym przecinają się promienie załamanie (w przypadku soczewki skupiającej) lub ich przedłużenia (w przypadku soczewki rozpraszającej - jest to ognisko pozorne). Zdolność skupiająca soczewki określa się przez podanie odwrotności ogniskowej (1/f). Nieformalną jednostką jest dioptria (D) - dodatnia oznacza soczewkę skupiającą, natomiast ujemna - soczewkę rozpraszającą.

Obraz powstający w soczewce konstruuje się na podstawie biegu trzech promieni -pierwszego, równoległego do osi soczewki (po załamaniu przechodzi przez ognisko F₂), drugiego, przechodzącego przez środek optyczny soczewki (nie zmienia kierunku) i trzeciego, przechodzącego przez ognisko F₁ (po załamaniu biegnie równolegle do osi soczewki).

W soczewce skupiającej może powstać obraz rzeczywisty, odwrócony i pomniejszony (gdy odległość przedmiotu jest większa od ogniskowej) lub obraz pozorny, prosty i powiększony (odległość przedmiotu mniejsza niż ogniskowa). W soczewce rozpraszającej powstaje natomiast obraz pozorny, prosty i pomniejszony. Zależność pomiędzy ogniskową, a odległością soczewki od przedmiotu (a) i odległością soczewki od obrazu (b) podaje równanie soczewki:

• Metody wyznaczania ogniskowych soczewek

1. Wyznaczanie ogniskowej w oparciu o równanie soczewki

Metoda polega na znalezieniu takiego położenia soczewki na ławie optycznej, w którym na ekranie obserwuje się obraz ostry i powiększony. Ogniskowa wyznaczana jest dzięki pomiarowi odległości soczewki od przedmiotu i od ekranu.

2. Metoda Bessela

Metoda polega na wyznaczeniu dwóch położeń soczewki na ławie optycznej, w których na ekranie obserwujemy obraz ostry (pomniejszony i powiększony). Mierząc odległość między tymi położeniami soczewki (d) oraz znając odległość przedmiotu od ekranu możemy wyznaczyć ogniskowa z zależności:

3. Ogniskowa układu soczewek

Ogniskową układu soczewek, zbudowanego z dwóch cienkich soczewek umieszczonych w odległości δ można wyznaczyć z zależności:

Gdy soczewki znajdują się blisko siebie ostatni człon powyższego równania można zaniedbać.

• Wady soczewek

• Aberracja sferyczna - widoczna, gdy na soczewkę pada szeroka wiązka promieni. Polega ona na tym, że promienie przyosiowe i brzegowe są załamywane w odmienny sposób - brzegowe silnej. W efekcie powstają dwa osobne ogniska dla promieni przyosiowych i brzegowych (ognisko promieni brzegowych znajduje się bliżej soczewki).

• Aberracja chromatyczna - jest związana z dyspersją. Polega ona na odmiennym sposobie załamania różnych barw widmowych światła (składowych o różnych długościach fal) przez to samo miejsce soczewki. W efekcie powstają osobne ogniska dla fal o różnych długościach.

• Astygmatyzm - wada, polegająca na powstawaniu nieostrego, rozmytego obrazu w soczewce. Astygmatyzm pojawia się, gdy wiązka promieni świetlnych pada na soczewkę pod dużym kątem względem osi głównej soczewki (różne części wiązki załamywane są w innych fragmentach soczewki o różnych warunkach geometrycznych)

2. Plan pracy

1. Zanotować położenie przedmiotu i ekranu

2. Dla wybranego położenia ekranu trzykrotnie wyznaczyć położenie soczewki, dla którego widoczny jest ostry, powiększony obraz

3. Obrócić soczewkę o 180°, wyznaczyć trzykrotnie położenie soczewki, takie jak w pkt 2

4. Pomiary z pkt 2 i 3 powtórzyć dla 4 innych położeń ekranu

5. Dla tych samych położeń ekranu wyznaczyć (po 3 razy dla każdego) położenia soczewki, w których obserwuje się obraz powiększony i obraz pomniejszony (metoda Bessela)

6. Na ławie optycznej zamocować układ soczewek i wykonać dla niego pomiary analogiczne do pomiarów z pkt 5

7. Na ławie optycznej umieścić grubą soczewkę, zanotować jej położenie

8. Montować kolejno osłony dla promieni brzegowych, pośrednich i przyosiowych i dla każdej z osłon wyznaczać położenie ekranu, w którym widoczny jest ostry obraz

9. Umieścić przed przedmiotem filtr (najpierw niebieski, potem czerwony) i wyznaczyć położenie ekranu, w którym widoczny jest wyraźny obraz.

10. Powtórzyć czynności z punktu 9, zakładając dodatkowo na soczewkę osłonę dla promieni przyosiowych.

11. Nałożyć matówkę z siatką prostopadłych linii i wyznaczyć położenie soczewki, w którym na ekranie widoczne są tylko kreski pionowe, a następnie tylko poziome

3. Wyniki

1. Wyznaczanie ogniskowej soczewki skupiającej na podstawie równania soczewki

W tej części ćwiczenia wykonano pomiary położenia soczewki, w którym uzyskano obraz ostry i powiększony. Położenie przedmiotu ( oznaczone jako p) jest stałe, podobnie jak położenie ekranu ( e). Położenie soczewki zmierzono trzykrotnie (pomiary oznaczone jako s₁), a następnie obrócono soczewkę o 180 ° i ponownie zmierzono położenie soczewki (s₂).

Wyniki pomiaru I przedstawia tabela:

położenie przedmiotu (p) [m]	położenie ekranu (e) [m]	położenie soczewki (s1) [m]	położenie soczewki po obrocie (s2) [m]
0,15	0,8	0,308	0,323
				0,307	0,323
				0,305	0,321

Wartość średnią dla s₁ i s₂ obliczono, korzystając ze wzoru:

Natomiast wartość s_średnie obliczono, korzystając ze wzoru:

Niepewność pomiaru położenia soczewek dla wartości średniej obliczono korzystając ze wzoru:

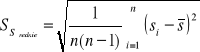
Odległości soczewka - przedmiot(a) i soczewka - ekran (b) obliczono ze wzorów:

Niepewność pomiaru odległości soczewka - przedmiot i soczewka - ekran policzono jako sumę niepewności systematycznej (czyli niepewności pomiaru położenia przedmiotu/ekranu i niepewności pomiaru położenia soczewki) i całkowitej niepewności przypadkowej, zgodnie z wzorem:

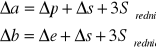
przy czym za Δp = Δe =Δs przyjęto 0,001 m ( wynika to z podziałki na ławie optycznej).

Dla pierwszego pomiaru wartości s₁,s₂ i s_średnie wynoszą odpowiednio:

Natomiast wartości a i b:

A zatem wyniki obliczeń:

s_średnie = (0,314 ± 0,004) m

a = (0,164 ± 0,014) m

b = (0,486 ± 0,014) m

Ogniskową soczewki wyznaczono, przekształcając równanie soczewki do postaci:

Natomiast niepewność oszacowano metodą różniczki zupełnej:

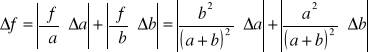
Wynoszą one odpowiednio:

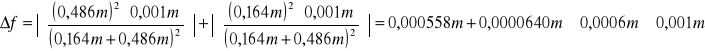
f = (0,123 ± 0,001) m

Wyniki pozostałych obliczeń wraz z danymi zestawiono w tabelach:

Pomiar II

położenie przedmiotu (p) [m]	położenie ekranu (e) [m]	położenie soczewki (s1) [m]	położenie soczewki po obrocie (s2) [m]
0,15	0,9	0,317	0,297
				0,319	0,300
				0,316	0,300

Pomiar III

położenie przedmiotu (p) [m]	położenie ekranu (e) [m]	położenie soczewki (s1) [m]	położenie soczewki po obrocie (s2) [m]
0,15	1	0,309	0,290
				0,310	0,292
				0,311	0,291

Pomiar IV

położenie przedmiotu (p) [m]	położenie ekranu (e) [m]	położenie soczewki (s1) [m]	położenie soczewki po obrocie (s2) [m]
0,15	1,07	0,296	0,304
				0,297	0,312
				0,297	0,307

Pomiar V

położenie przedmiotu (p) [m]	położenie ekranu (e) [m]	położenie soczewki (s1) [m]	położenie soczewki po obrocie (s2) [m]
0,15	1,2	0,285	0,303
				0,283	0,304
				0,284	0,302

Średnia arytmetyczna ogniskowej uzyskanego dla 5 pomiarów wynosi:

f = (0,1246 ± 0,0010)m ≈ (0,125 ± 0,001) m

Zdolność skupiająca tej soczewki (podana na opakowaniu) wynosi + 8,00 D. Ponieważ zdolność skupiająca soczewki określona jest jako Z= 1/f → f =1/ Z = 0,125 m. Wartość wyznaczona na podstawie równania soczewki jest zatem zgodna z wartością rzeczywistą.

2. Wyznaczanie ogniskowej soczewki skupiającej metodą Bessela

W tej części ćwiczenia, dla ustalonego położenia ekranu wyznaczano trzykrotnie położenie soczewki, w którym na ekranie widoczny jest ostry, powiększony obraz (s₁) oraz położenie, dla którego obraz jest ostry i pomniejszony (s₂).

położenie przedmiotu (p) [m]	położenie ekranu (e) [m]	Obraz powiększony (s1) [m]	Obraz pomniejszony (s2) [m]
0,15	0,8	0,309	0,616
				0,310	0,616
				0,309	0,617

Wartości średnie dla s₁ i s₂ oraz ich niepewności obliczono, korzystając ze wzorów:

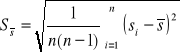
Odległość pomiędzy położeniami soczewki i jej niepewność obliczono:

Odległość między przedmiotem a ekranem obliczono:

(Δp = Δe =Δs₁ = Δs₂ = 0,001 m)

Dla I pomiaru:

Ogniskową soczewki wyznaczono korzystając z zależności:

Natomiast niepewność wyznaczania ogniskowej soczewki:

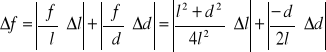
Dla I pomiaru:

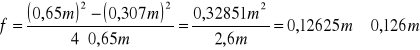
f = (0,126 ± 0,002) m

Wyniki dla pozostałych pomiarów wraz z danymi przedstawiono poniżej:

Pomiar II

położenie przedmiotu (p) [m]	położenie ekranu (e) [m]	Obraz powiększony (s1) [m]	Obraz pomniejszony (s2) [m]
0,15	0,9	0,300	0,724
				0,298	0,724
				0,300	0,722

Pomiar III

położenie przedmiotu (p) [m]	położenie ekranu (e) [m]	Obraz powiększony (s1) [m]	Obraz pomniejszony (s2) [m]
0,15	1	0,294	0,843
				0,292	0,842
				0,293	0,840

Pomiar IV

położenie przedmiotu (p) [m]	położenie ekranu (e) [m]	Obraz powiększony (s1) [m]	Obraz pomniejszony (s2) [m]
0,15	1,07	0,287	0,91
				0,286	0,906
				0,285	0,903

Pomiar V

położenie przedmiotu (p) [m]	położenie ekranu (e) [m]	Obraz powiększony (s1) [m]	Obraz pomniejszony (s2) [m]
0,15	1,2	0,282	1,041
				0,283	1,042
				0,284	1,044

Wartość ogniskowej policzona jako średnia arytmetyczna uzyskanych wyników wynosi:

f = (0,1255 ± 0,0022) m ≈ (0,125 ± 0,002)m

Wartości ogniskowych wyznaczonych z równania soczewki oraz metodą Bessela są do siebie zbliżone i porównywalne w granicach niepewności pomiarowych. Są również zgodne z wartością obliczoną ze zdolności skupiającej soczewki.

3. Wyznaczanie ogniskowej układu soczewek oraz ogniskowej soczewki rozpraszającej

W tej części ćwiczenia przy ustalonym położeniu ekranu wyznaczano położenie układu soczewek, w którym na ekranie obserwowany był obraz powiększony i pomniejszony. Układ ten był złożony z badanej wcześniej soczewki skupiającej oraz soczewki rozpraszającej. Wyniki ilustruje tabela:

Pomiar I

położenie przedmiotu (p) [m]	położenie ekranu (e) [m]	Obraz powiększony (s1) [m]	Obraz pomniejszony (s2) [m]
0,15	0,9	0,379	0,636
				0,382	0,634
				0,383	0,637

Pomiary rozpoczęto od położenia ekranu e = 0,9 m, a nie (jak w poprzednich przypadkach) od położenia ekranu e = 0,8 m, ponieważ dla takiego położenia ekranu nie można było uzyskać odpowiednich obrazów. Wynika to z faktu, że dla metody Bessela odległość l (ekran - przedmiot) musi być większa niż 4f. Po obliczeniu ogniskowej takiego układu wykaże, że dla położenia ekranu e = 0,8 m warunek ten nie był spełniony.

Obliczając ogniskową układu soczewek metoda Bessela skorzystano z tych samych wzorów, co w punkcie 3.b. Ponadto wyznaczono ogniskową soczewki rozpraszającej, korzystając ze wzorów

→

Natomiast niepewność obliczono metoda różniczki zupełnej:

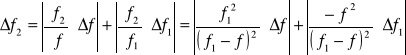
Dla I pomiaru:

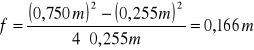
Ogniskowa soczewki rozpraszającej:

Wyniki dla pomiaru I:

s₁ = (0,381 ± 0,001) m

s₂ = (0,636 ± 0,001) m

l = (0,750 ± 0,002) m

d = (0,255 ± 0,008) m

f = (0,166 ± 0,002) m

f _r = (-0,507 ± 0,050) m

Wyniki pozostałych pomiarów wraz z danymi:

położenie przedmiotu (p) [m]	położenie ekranu (e) [m]	Obraz powiększony (s1) [m]	Obraz pomniejszony (s2) [m]
0,15	1	0,366	0,765
				0,364	0,766
				0,365	0,765

Pomiar II

położenie przedmiotu (p) [m]	położenie ekranu (e) [m]	Obraz powiększony (s1) [m]	Obraz pomniejszony (s2) [m]
0,15	1,07	0,356	0,826
				0,356	0,825
				0,357	0,828

Pomiar III

Pomiar IV

położenie przedmiotu (p) [m]	położenie ekranu (e) [m]	Obraz powiększony (s1) [m]	Obraz pomniejszony (s2) [m]
0,15	1,2	0,341	0,972
				0,342	0,973
				0,344	0,972

Wartość średnia ogniskowej takiego układu wynosi f = (0, 167 ± 0,002) m.

Wartość średnia ogniskowej soczewki rozpraszającej wynosi: f = (-0,495 ± 0,049) m.

Zdolność skupiająca tej soczewki (podana na opakowaniu) wynosi -2 D. Wartość ogniskowej obliczonej ze zdolności skupiającej wynosi -0,5m, a wartość ogniskowej układu ( 8D -2D = 6D) około 0,1667m. Wartości uzyskane w ćwiczeniu są zbliżone do wartości rzeczywistych i zgodne z nimi w granicach niepewności pomiarowych.

Gdy ekran znajdował się w położeniu e = 0,8 m, odległość ekran - przedmiot wynosiła 0,65 m. Aby na ekranie można było obserwować ostry obraz musi być spełniony warunek l > 4f.

Wartość 4f wynosi około 0,668 m. Warunek ten nie jest więc spełniony dla położenia ekranu

e =0,8m, dlatego też nie można było wykonać odpowiednich pomiarów.

4. Aberracja sferyczna

W tej części ćwiczenia należało najpierw ustalić położenie grubej soczewki, dla którego na ekranie pojawiał się ostry, powiększony obraz. Następnie na soczewkę nakładano kolejne przesłony i poruszając ekranem wyznaczano takie jego położenie, w którym widoczny był ostry obraz. Wartości uzyskane w ćwiczeniu:

• położenie soczewki bez przesłon - 0,434 m

• położenie ekranu dla soczewki z przesłoną dla promieni brzegowych - 0,876 m

• położenie ekranu dla soczewki z przesłoną dla promieni pośrednich - 0,974 m

• położenie ekranu dla soczewki z przesłona dla promieni przyosiowych - 1,094 m

Korzystając z przekształconego równania soczewki, podanego w punkcie 3.a.obliczono wartości ogniskowych oraz ich niepewności (wzór również w punkcie 3.a), uzyskując następujące wyniki:

• dla promieni brzegowych f_b = (0,1729 ± 0,0005) m

• dla promieni pośrednich f_poś = (0,1861 ± 0,0006) m

• dla promieni przyosiowych f_p = (0,1986 ± 0,0006) m

Miarą aberracji jest różnica ogniskowych dla promieni przyosiowych i brzegowych, która w tym wypadku wynosi 0,0257 m = 2,57 cm. Niepewność pomiarowa tej wielkości to suma niepewności Δf_p i Δf_b, wynosząca 0,0011m. A zatem wartość określająca aberrację sferyczną w tym wypadku wynosi (0,0257 ± 0,0011) m

5. Aberracja chromatyczna

W tej części ćwiczenia, przy ustalonym położeniu soczewki i nałożonym filtrze, należało wyznaczyć położenie ekranu, przy którym widoczny jest ostry obraz. Wykonano również pomiary położenia ekranu przy nałożonym filtrze i osłonie dla promieni przyosiowych. Wartości uzyskane w ćwiczeniu:

• położenie soczewki - 0,434 m

• położenie ekranu przy filtrze niebieskim - 1,040 m

• położenie ekranu przy filtrze niebieskim z przesłoną - 1,125m

• położenie ekranu przy filtrze czerwonym -1,051 m

• położenie ekranu przy filtrze czerwonym z przesłoną -1,151 m

Ogniskowe wyznaczono analogicznie do ogniskowych przy aberracji sferycznej (ponieważ wyznaczono tylko jedno położenie ekranu i soczewki, trzeba było skorzystać z metody opartej na równaniu). Wynoszą one odpowiednio:

• z filtrem niebieskim f _n = (0,1934 ± 0,0006)m

• z filtrem niebieskim i przesłoną f_n+p= (0,2013 ± 0,0006)m

• z filtrem czerwonym f_cz = (0,1945 ± 0,0006) m

• z filtrem czerwonym i przesłoną f_cz+p= (0,2034 ± 0,0006) m

Miarą aberracji chromatycznej jest w tym przypadku różnica ogniskowych dla światła czerwonego i niebieskiego, która wynosi 0,0011m = 0,11 cm =1,1 mm. Niepewność tego pomiaru wynosi natomiast 0,0012 m.

6. Astygmatyzm

W tej części ćwiczenia posługiwano się matówką z naniesioną siatką prostopadłych linii. Przy ustalonym położeniu ekranu wyznaczono takie położenia soczewki, w których na ekranie widoczne były tylko linie pionowe (P₁) oraz tylko linie poziome (P₂). Uzyskane wyniki:

• położenie ekranu - 1,040 m

• P₁ (linie pionowe) - 0,370 m

• P₂ (linie poziome) - 0,426 m

Miarą pełnego astygmatyzmu jest różnica położeń P₁ i P₂. Wynosi ona dla tego przypadku 0,0056 m = 0,56 cm =5,6 mm. Niepewność tego pomiaru to suma niepewności systematycznych związanych z przyrządem miarowym, wynosi ona 0,002m. Astygmatyzm charakteryzuje więc wielkość (0,0056 ± 0,002) m

7. Dyskusja wyników i niepewności

Celem ćwiczenia było wyznaczenie wartości ogniskowej soczewki skupiającej metodą opartą na równaniu soczewki oraz metodą Bessela. Uzyskane wyniki są zgodne w granicach niepewności pomiarowych między sobą oraz z wynikiem, uzyskanym z przeliczenia zdolności skupiającej soczewki. Metoda Bessela pozwala zazwyczaj na uzyskanie wyników dokładniejszych, ale w tym przypadku również metoda równania soczewki pozwoliła otrzymać poprawny wynik

Ćwiczenie miało również na celu wyznaczenie wartości ogniskowej dla układu dwóch soczewek oraz wartości ogniskowej dla soczewki rozpraszającej metodą Bessela. Również w tym wypadku uzyskane wartości są zgodne w granicach niepewności z wartościami obliczonymi na podstawie zdolności skupiającej soczewki (-ek).

W ćwiczeniu wykonano również badanie wad soczewek. W przypadku aberracji sferycznej uzyskane wyniki potwierdzają silniejsze załamywanie promieni brzegowych (ognisko znajduję się bliżej, z czego wynika mniejsza wartość ogniskowej). Promienie pośrednie załamywane są słabiej niż brzegowe, ale silniej niż przyosiowe (stąd pośrednia wartość ogniskowej), natomiast promienie przyosiowe załamywane są najsłabiej (ognisko położone jest najdalej).

Wyniki uzyskane w punkcie 3.e potwierdzają istnienie zjawiska aberracji chromatycznej. Ognisko dla światła czerwonego znajduję się dalej niż dla światła niebieskiego. Jest to zgodne z przewidywaniami, ponieważ światło czerwone załamywane jest słabiej od światła niebieskiego.

W ćwiczeniu potwierdzono również istnienie astygmatyzmu. Wyznaczone położenia soczewki, w których widoczne są tylko linie pionowe i tylko linie poziome, a właściwie odległość między tymi położeniami, jest wielkością zależną od kąta padania promieni świetlnych.

Niepewności pomiarowe w ćwiczeniu wynikają z niepewności przyrządów pomiarowych, niedokładności wykonywanych pomiarów i niedokładności odczytywanych wyników. Ponadto ostrość uzyskiwanego na ekranie obrazu jest subiektywna. Pewnym utrudnieniem była również konieczność wykonania wielu pomiarów, w efekcie zmniejszająca dokładność obserwatorów ( i tak obarczoną błędem).

W załączeniu:

1. Karty wyników z zajęć

Bibliografia:

1. A. Magiera, I Pracownia Fizyczna, UJ

2. T.Dryński, Ćwiczenia laboratoryjne z fizyki, PWN

3. H.Szydłowki, Pracownia fizyczna, PWN

Rysunki soczewek na str. 2 pochodzą z Internetu:

1. http://www.bryk.pl/teksty/liceum/fizyka/zjawiska_optyczne/10013-optyka.html

2. http://www.iwiedza.net/wiedza/113.html

3

s_średnie = (0,308 ± 0,004) m

a = (0,158 ± 0,014) m

b = (0,592 ± 0,014) m

f = (0,125 ± 0,001) m

Soczewka skupiająca ↑ i rozpraszająca ↓

s_średnie = (0,300 ± 0,004) m

a = (0,150 ± 0,015) m

b = (0,699 ± 0,015) m

f = (0,124 ± 0,001) m

s_średnie = (0,302 ± 0,003) m

a = (0,152 ± 0,010) m

b = (0,768 ± 0,010) m

f = (0,127 ± 0,001) m

s_średnie = (0,294 ± 0,004) m

a = (0,144 ± 0,015) m

b = (0,907 ± 0,015) m

f = (0,124 ± 0,001) m

Wyniki obliczeń:

s₁ = (0,309 ± 0,0004) m

s₂ = (0,616 ± 0,0004) m

d = (0,307 ± 0,0044) m

l = (0,650 ± 0,002) m

s₁ = (0,299 ± 0,001) m

s₂ = (0,723 ± 0,001) m

d = (0,424 ± 0,006) m

l = (0,750 ± 0,002) m

f = (0,128 ± 0,001)m

s₁ = (0,293 ± 0,001) m

s₂ = (0,842 ± 0,0004) m

d = (0,549 ± 0,006) m

l = (0,850 ± 0,002) m

f = (0,124 ± 0,002)m

s₁ = (0,286 ± 0,001) m

s₂ = (0,906 ± 0,002) m

d = (0,620 ± 0,001) m

l = (0,920 ± 0,002) m

f = (0,125 ± 0,003) m

s₁ = (0,283 ± 0,001) m

s₂ = (1,042 ± 0,001) m

d = (0,759 ± 0,006) m

l = (1,050 ± 0,002) m

f = (0,125 ± 0,003) m

s₁ = (0,299 ± 0,001) m

s₂ = (0,723 ± 0,001) m

d = (0,424 ± 0,006) m

l = (0,750 ± 0,002) m

f = (0,128 ± 0,001)m

s₁ = (0,299 ± 0,001) m

s₂ = (0,723 ± 0,001) m

d = (0,424 ± 0,006) m

l = (0,750 ± 0,002) m

f = (0,128 ± 0,001)m

s₁ = (0,299 ± 0,001) m

s₂ = (0,723 ± 0,001) m

d = (0,424 ± 0,006) m

l = (0,750 ± 0,002) m

f = (0,128 ± 0,001)m

s₁ = (0,299 ± 0,001) m

s₂ = (0,723 ± 0,001) m

d = (0,424 ± 0,006) m

l = (0,750 ± 0,002) m

f = (0,128 ± 0,001)m

s₁ = (0,299 ± 0,001) m

s₂ = (0,723 ± 0,001) m

d = (0,424 ± 0,006) m

l = (0,750 ± 0,002) m

f = (0,128 ± 0,001)m

s₁ = (0,299 ± 0,001) m

s₂ = (0,723 ± 0,001) m

d = (0,424 ± 0,006) m

l = (0,750 ± 0,002) m

f = (0,128 ± 0,001)m

Wyniki obliczeń:

s₁ = (0,309 ± 0,0004) m

s₂ = (0,616 ± 0,0004) m

d = (0,307 ± 0,0044) m

l = (0,650 ± 0,002) m

Wyniki obliczeń:

s₁ = (0,309 ± 0,0004) m

s₂ = (0,616 ± 0,0004) m

d = (0,307 ± 0,0044) m

l = (0,650 ± 0,002) m

Wyniki obliczeń:

s₁ = (0,309 ± 0,0004) m

s₂ = (0,616 ± 0,0004) m

d = (0,307 ± 0,0044) m

l = (0,650 ± 0,002) m

Wyniki obliczeń:

s₁ = (0,309 ± 0,0004) m

s₂ = (0,616 ± 0,0004) m

d = (0,307 ± 0,0044) m

l = (0,650 ± 0,002) m

Wyniki obliczeń:

s₁ = (0,309 ± 0,0004) m

s₂ = (0,616 ± 0,0004) m

d = (0,307 ± 0,0044) m

l = (0,650 ± 0,002) m

Wyniki obliczeń:

s₁ = (0,309 ± 0,0004) m

s₂ = (0,616 ± 0,0004) m

d = (0,307 ± 0,0044) m

l = (0,650 ± 0,002) m

Wyniki obliczeń:

s₁ = (0,309 ± 0,0004) m

s₂ = (0,616 ± 0,0004) m

d = (0,307 ± 0,0044) m

l = (0,650 ± 0,002) m

s₁ = (0,365 ± 0,0006) m

s₂ = (0,7653 ± 0,0003) m

d = (0,400 ± 0,005) m

l = (0,850 ± 0,002) m

f = (0,165 ± 0,002)m

f₂ = (-0,512 ± 0,050) m

s₁ = (0,3563 ± 0,0003) m

s₂ = (0,826 ± 0,001) m

d = (0,470 ± 0,006) m

l = (0,920 ± 0,002) m

f = (0,170 ± 0,002)m

f₂ = (-0,472 ± 0,045) m

s₁ = (0,342 ± 0,001) m

s₂ = (0,9723 ± 0,0003) m

d = (0,630 ± 0,006) m

l = (1,050 ± 0,002) m

f = (0,168 ± 0,002)m

f₂ = (-0,488 ± 0,051) m

---