Rachunek Prawdopodobieństwa

Zestaw nr3.

Zadanie 3.1.

Obliczyć A i B, aby funkcja F(x) była dystrybuantą ciągłej zmiennej losowej X:

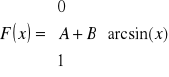
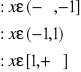
Wyznaczyć gęstość prawdopodobieństwa zmiennej losowej X. Wykreślić funkcje F(x) i f(x). Obliczyć prawdopodobieństwo przyjmowania przez zmienną losową X wartości z przedziału (0,
).

Rozwiązanie

Na wstępie przypomnę co to jest dystrybuanta. A mianowicie Dystrybuantą mówi nam jakie jest prawdopodobieństwo, że zmienna losowa X przyjmie wartość mniejszą od x:

Dystrybuanta ma następujące własności (więc badana zadana funkcja też musi je mieć):

1.
, jak widać nasza funkcja spełnia ten warunek.

2.
, ten warunek też jest spełniony.

3. Funkcja musi być niemalejąca.

Aby nasz funkcja była niemalejąca musi być spełniona nierówność:

na przedziale (-1,1)

Wiemy, że funkcja arcsin(x) jest rosnąca, więc B>0, w przeciwnym przypadku funkcja

byłaby malejąca i nie spełniałaby warunków.

Tworzymy układ równań:

= >

= >

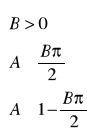
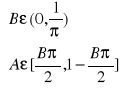
3 Dystrybuanta jest funkcją lewostronnie ciągłą.

W naszym wypadku funkcja musi spełniać następujący warunek:

, więc

=>

Aby
była dystrybuantą ciągłej zmiennej losowej, to też musi być ciągła, więc:

=>

Biorąc pod uwagę ten i poprzedni warunek otrzymujemy układ równań:

=>

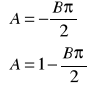
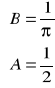
Co daje ostateczny wynik:

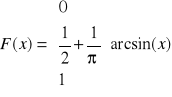
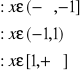
Kolejnym krokiem w zadaniu jest wyliczenie gęstości prawdopodobieństwa. Liczymy ją zgodnie za wzorem:

, o ile istnieje liczona różniczka.

Wiemy, że nasza funkcja jest ciągła, więc posiada ona pochodną.

Obliczeń dokonujemy na przedziałach:

1

2

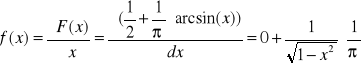
, nie trzeba tu dodatkowych

założeń dla x ponieważ przedział dla niego jest odpowiedni.

3

Ostatecznie otrzymujemy:

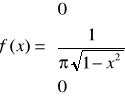
Ostatnim punktem zadania jest wyliczenie poniższego prawdopodobieństwa:

Wykres:

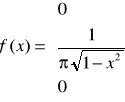
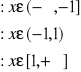
Wykres:

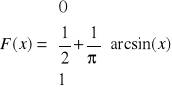
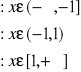
Zadanie 3.2.

By funkcja
była gęstością prawdopodobieństwa, musi zachodzić następująca zależność:

a co za tym idzie:

.

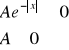
W tym momencie zauważamy, że jeśli istnieją odpowiednie całki, to:

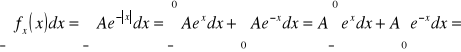
By
była gęstością prawdopodobieństwa musi oczywiście zachodzić następujący warunek:

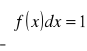
(czyli pole pod całą krzywą musi być równe 1)

a co za tym idzie:

2A=1

Wartość ta spełnia warunek bycia większym-równym od 0, czyli

Czyli otrzymujemy następujący wykres:

Dystrybuanta

Dany mamy wzór (bez względu na to, gdzie znajdujemy się na osi 0X):

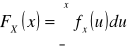
mamy zatem:

- dla
(przy założeniu istnienia odpowiednich funkcji całkowych)

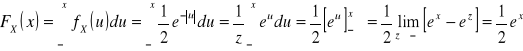
- dla
(przy założeniu istnienia odpowiednich funkcji całkowych)

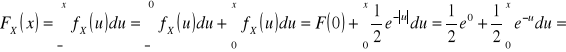
Otrzymujemy zatem:

Czyli otrzymujemy następujące wykresy funkcji:

Co sumarycznie daje nam:

Zadanie 3.3.

Czas pracy [w setkach godzin] do chwili przepalenia się lampy elektronowej jest zmienną losową

o gęstości prawdopodobieństwa:

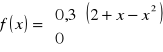
Znaleźć dystrybuantę zmiennej losowej X. Narysować funkcję f(x) i F(x). Obliczyć prawdopodobieństwo, że lampa przepali się przed upływem 100 godzin oraz prawdopodobieństwo, że lampa przepali się między 50 a 100 godziną.

Rozwiązanie:

Korzystając ze wzoru:

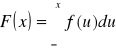
- Dla

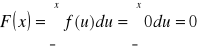
- Dla

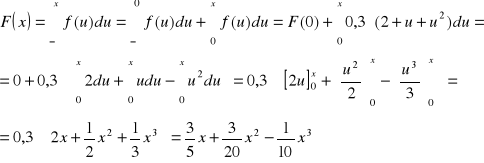
- Dla

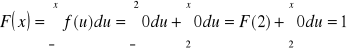
Dystrybuanta F(x) zmiennej losowej X

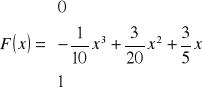
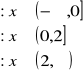
Wykres gęstości f(x) prawdopodobieństwa:

Wykres dystrybuanty F(x):

Zadanie 3.4.

Zmienna losowa X ma gęstość prawdopodobieństwa f(x) daną wzorem:

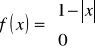
Wyznaczyć dystrybuantę F(x) zmiennej losowej X oraz podać wykres. Obliczyć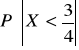
.

Rozwiązanie:

Zapisujemy

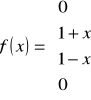
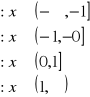
Korzystając ze wzoru:

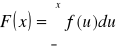
- Dla

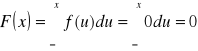
- Dla

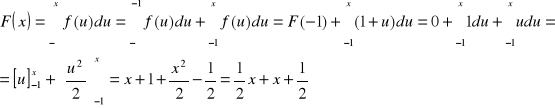
- Dla

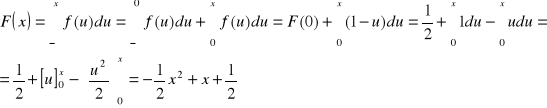
- Dla

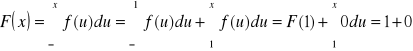
Dystrybuanta F(x) zmiennej losowej X

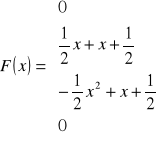
Dystrybuanta F(x) zmiennej losowej X - wykres:

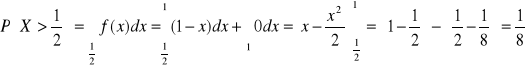
Zadanie 3.5.

Zmienna losowa X ma dystrybuantę F(x) daną wzorem:

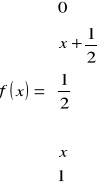
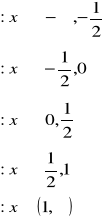
Wyznaczyć dystrybuantę F(x) zmiennej losowej X oraz podać wykres. Obliczyć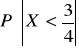
.

Rozwiązanie:

Wykres F(x):

Korzystając ze wzoru:

- Dla

- Dla

- Dla

- Dla

- Dla

Gęstość f(x):

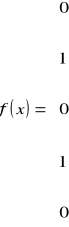
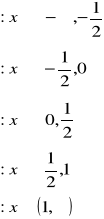
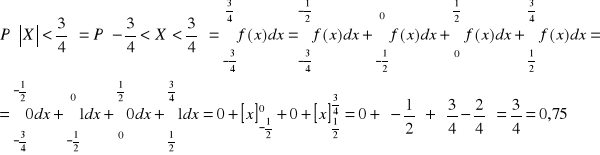
Zadanie 3.6.

Mamy dystrybuantę zmiennej losowej X

Z zależności:

wiemy, że:

Z powyższych odczytujemy histogram funkcji rozkładu prawdopodobieństwa:

I sporządzamy odpowiedni wykres P(X<x) jako funkcji zmiennej x:

Zadanie 3.7.

Na zbiorze liczb rzeczywistych określamy funkcję gęstości w sposób następujący:

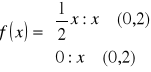
Znaleźć dystrybuantę zmiennej losowej X i narysować jej wykres.

Wiemy, że:

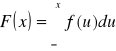
Wystarczy policzyć całki na wszystkich przedziałach:

1

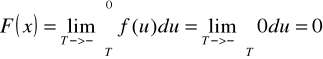
2

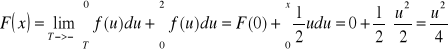
3

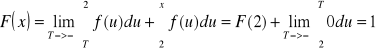
Ostateczny wynik to:

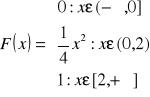
Wykres, dla powyższej funkcji

---