OBLICZANIE KRZYWEJ PŁYWU

SPOSÓB RACHUNKOWY Z WYKORZYSTANIEM

KALKULATORA

Odmiana uproszczonej metody harmonicznej, omówiona w każdym tomie ATT, została opracowana z myślą o wykorzystaniu kalkulatora.

W przypadku obliczania pełnej 24-godzinnej przepowiedni zapewne nie zrobimy tego szybciej niż w przypadku metody graficznej, uzyskamy jednak nieco dokładniejsze wyniki. Gdy jednak żądana przepowiednia obejmuje krótki okres czasu, metoda ta jest prawdopodobnie szybsza, a obliczanie przepowiedni dla niepełnych godzin - łatwiejsze.

Diagramy A i B oraz szczegółowa instrukcja, jak należy je wypełniać, są zawarte w każdym tomie ATT i będą pomocne przy obliczeniach.

Poniżej podano instrukcję wypełniania diagramów, a zawarty przykład wymaganą dokładność obliczeń (ilość miejsc po przecinku).

PRZYKŁAD

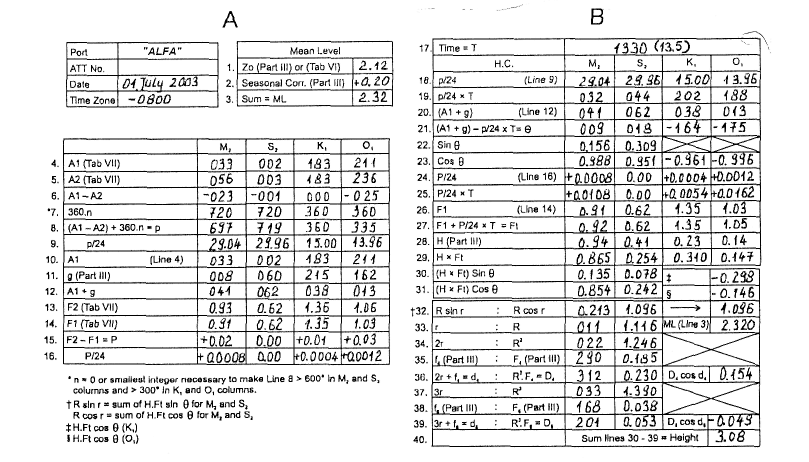
Obliczyć wysokość pływu w porcie „ALFA” dnia 01.07.2003 r. o godzinie 1330. W celu uproszczenia obliczeń podać również wysokości obliczone stosując sugerowane uproszczenia zawarte w uwagach pkt. 4, wariant a), b) i c).

Rys. 1 Formularze A i B do obliczania krzywej pływu metodą kalkulatorową

Instrukcja ramowa

1. Wypełnić formularz A zgodnie z podanymi poniżej instrukcjami szczegółowymi (Sekcja A).

2. Wypełnić formularz B wprowadzając wszystkie wymagane dane - wykonać szczegółowe instrukcje podane w Sekcji B.

3. Wypełnić formularz B uwzględniając uproszczenia podane w Uwagach, pkt. 4 (rys. 2).

4. Obliczyć poprawki płytkowodne.

5. Podać wynik.

SEKCJA A. Należy wypełnić dla każdego dnia żądanej przepowiedni.

1. Wpisać nazwę portu, jego numer podany w ATT, datę i czas strefowy.

2. Z części III ATT wypełnić:

Z₀ (lub z tabeli VI, jeżeli konieczne) ...........................................................wiersz l

Poprawka sezonowa (seasonal change) ......................................................wiersz 2

Wartość g⁰ .................................................................................................wiersz 11

3. Z tabeli VII ATT wypełnić:

Wartość A w żądanym dniu przepowiedni (A₁) ..................................wiersz 4 i 10

Wartość A w dniu następnym (A₂) .............................................................wiersz 5

Wartość F w żądanym dniu przepowiedni (F₁) .........................................wiersz 14

Wartość F w dniu następnym (F₂) .............................................................wiersz 13

4. Dodać wiersz l i 2, aby uzyskać średni poziom (ML) .....................................wiersz 3

5. Różnica A₁ - A₂ ...............................................................................................wiersz 6

6. Wartość 360° zwielokrotnioną w wymaganym stopniu „n” razy
   (uwaga poniżej 16 wiersza formularza A, oraz uwaga 5 na końcu
   instrukcji) .........................................................................................................wiersz 7

7. Suma wierszy 6 i 7, uzyskamy dobową szybkość zmian A (p) .......................wiersz 8

8. Iloraz p/24 ........................................................................................................wiersz 9

9. Suma wierszy 10 i 11 (A₁ + g⁰) ......................................................................wiersz 12

10. Różnica F₂ - F₁ (P), uzyskamy szybkość zmian F .........................................wiersz 15

11. Iloraz P/24 ......................................................................................................wiersz 16

SEKCJA B. Należy wypełnić dla każdego czasu przepowiedni.

12. Do wiersza 17 wpisać żądany czas (T). Jeżeli kalkulator nie posiada możliwości zamiany godzin/minut/sekund na dziesiętne godziny, to wprowadzić np. 1812 = 18,2.

13. Z części III ATT wypełnić:

Wartość H (uwzględnić zmiany sezonowe, jeżeli mają miejsce) .............wiersz 28

Wartość f₄ ...........................................................................wiersz 35, kolumna l

Wartość F₄ gdy brak danych, wstawić zero ........................wiersz 35, kolumna 2

Wartość f₆ ...........................................................................wiersz 38, kolumna l

Wartość F₆ ...........................................................................wiersz 38, kolumna 2

14. Z diagramu sekcji A przepisać:

p/24 (wiersz 9) ...........................................................................................wiersz 18

(A₁ + g⁰) (wiersz 12) ..................................................................................wiersz 20

P/24 (wiersz 16) .........................................................................................wiersz 24

F₁ (wiersz 14 lub bezpośrednio z tabeli VII ATT) ....................................wiersz 26

ML (wiersz 3) .........................................................................wiersz 33, kolumna 4

15. Pomnożyć p/24 · T ..........................................................................................wiersz 19

16. Odjąć (patrz uwaga 4) wiersz 19 od wiersza 20 w celu uzyskania wartości Θ w 21 wierszu.

17. W wierszu 22 tylko w kolumnach M₂ i S₂ wpisać wartości sinΘ.

18. Do wszystkich kolumn w wierszu 23 wpisać wartości cosΘ.

19. W wierszu 25 pomnożyć P/24 · T, a uzyskane wartości dodać do wiersza 26; uzyskamy w wierszu 27 wyinterpolowaną wartość F nazwaną dalej Ft.

20. Pomnożyć H (wiersz 28) przez Ft (wiersz 27) a wyniki wpisać do wiersza 29.

21. Pomnożyć wiersz 29 przez wiersz 22, a otrzymane wartości H · Ft · sinΘ wpisać odpowiednio w kolumnach M₂ i S₂ w wierszu 30.

22. Pomnożyć wiersz 29 przez wiersz 23, a otrzymane wartości H · Ft · cosΘ wpisać odpowiednio w kolumnach M₂, S₂, K₁ i O₁ w wierszu 31. Wynik dla K₁ wpisać do ostatniej kolumny wiersza 30.

W celu uproszczenia zapisu, poniżej stałe harmoniczne M₂, S₂, K₁ i O₁ będziemy oznaczać numerem kolumny, odpowiednio: l, 2, 3, i 4.

23. W wierszu 30 dodać wartości z l i 2 kolumny, a wynik wpisać w wierszu 32, do l kolumny (R sin r).

24. W wierszu 31 dodać wartości z l i 2 kolumny, a wynik wpisać w wierszu 32, do 2 kolumny (R cos r) oraz do kolumny 4.

25. Dysponując wartościami: R sin r i R cos r wstawić obliczone wartości r (wiersz 33, kolumna 1) i R (wiersz 33, kolumna 2).

26. W wierszu 34, do l kolumny wstawić wartość 2r, a w wierszu 37 wartość 3r.

27. W wierszu 34, do 2 kolumny wstawić wartość R², a w wierszu 37 wartość R³.

28. Dodać wartości wierszy 34 i 35, w l kolumnie, a wynik wpisać w wierszu 36 (d₄).

29. Dodać wartości, wierszy 37 i 38, w l kolumnie, a wynik wpisać w wierszu 39 (d₆).

30. Pomnożyć wartości wierszy 34 i 35, w 2 kolumnie, a wynik wpisać w wierszu 36 (D₄).

31. Pomnożyć wartości wierszy 37 i 38, w 2 kolumnie, a wynik wpisać w wierszu 39 (D₆).

32. Wykonać mnożenie D₄ · cos d₄, a wynik wpisać w wierszu 36, do kolumny 4.

33. Wykonać mnożenie D₆ · cos d₆, a wynik wpisać w wierszu 39, do kolumny 4.

34. Sumę wartości liczbowych 4 kolumny wierszy 30, 31, 32, 33, 36 i 39 wpisać w wierszu 40.

UWAGI:

1. Zaleca się, aby wyniki dokonanych obliczeń zostały przedstawione graficznie, np. na papierze milimetrowym bądź w kratkę. Pojedyncza przepowiednia rzadko przedstawia dla nas wartość, gdyż nie daje wskazówek odnośnie prędkości wznoszenia bądź opadania pływu, a w niektórych przypadkach nawet, czy jest to czas wznoszenia bądź opadania.

2. Chociaż poszczególne kratki w diagramach umożliwiają zapis każdego kroku obliczeń, to możliwości kalkulatora i wprawa operatora mogą umożliwić zostawienie kilku kratek pustych, lub wprowadzenia ich do pamięci. Mając możliwość zamiany współrzędnych biegunowych na prostokątne możemy przejść bezpośrednio z wiersza 17 do 31 bez pośrednich zapisów i uniknąć dwuznaczności ćwiartki.

3. W wielu przypadkach interpolacje między F1 i F2 można przeprowadzić z wystarczającą dokładnością „na oko”, umożliwiając tym samym pominięcie wierszy 13, 14, 15, 16, 24 i 25.

4. W celu uproszczenia obliczeń, można stosować podane poniżej przybliżenia (lub przy programowaniu ograniczyć ilość kolejnych działań i/lub pamięć). Wskazana kolejność sugeruje ich wpływ na dokładność obliczeń, przy czym pierwsze przybliżenie (a) w najmniejszym stopniu zniekształca wynik. Na rysunku 2 przedstawiono trzy warianty formularza B wypełnionego z uwzględnieniem proponowanych poniżej uproszczeń.

1. Na formularzu A pominąć wiersze od 4 do 9, a do wiersza 18 wprowadzić następujące prędkości:

M₂ . 29,0°/h

S₂ 30,0°/h

K₁ 15,0°/h

O₁ 13,9°/h

2. Podobnie jak powyżej, ale następujące prędkości:

M₂

S₂ 29,32°/h

K₁

O₁ 14,66°/h, tzn. połowę powyższej wartości

3. 
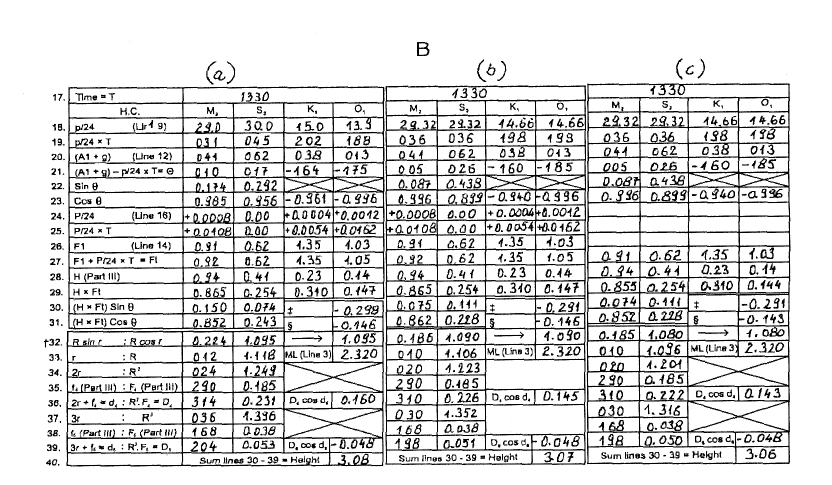
   Pominąć interpolację F. W tym celu opuścić wiersze: 13, 14, 15, 16, 24, 25 i 26, a wartość Ft = F wpisać bezpośrednio z tabeli VII ATT w wierszu 27.

Rys. 2 Warianty formularza B z uwzględnieniem uproszczeń: (a), (b), (c)

- por. uwagi, punkt 4

5. Interpolacja pomiędzy wartościami A i F zawartymi w tabeli VII.
   Szybkość zmiany dobowego kąta pływu (A) w ciągu godziny dla każdej składowej, możemy obliczyć z kolejnych następujących po sobie wartości podanych w tabeli, pamiętając o dodaniu do wartości tablicowych odpowiedniej wielokrotności 360°. W celu upewnienia się, że szybkości te są zbliżone do wartości astronomicznych poszczególnych składowych, tzn. 30°/h dla M₂ i S₂, oraz 15°/h dla K₁ i O₁, można to zrobić w sposób następujący:

Prędkość dobowa (p) = (A₁ + 360° · n) - A₂

gdzie n = 0 lub najmniejsza liczba całkowita zapewniająca p > 600 w przypadku M₂ i S₂ i p > 300 dla K₁ i O₁.

Wówczas dla każdej z czterech składowych:

At = A₁ - (T · p) : 24

Wartości A w tabeli VII są podane w formie umożliwiającej prostotę działań arytmetycznych w wersji graficznej pierwszego wydania uproszczonej metody harmonicznej (podana wartość to 360° minus wartość astronomiczna). Z tego powodu drugi człon w wyrażeniu powyższym odejmujemy.

Interpolacja dla F dla zadanego czasu jest prostsza:

Ft = F₁ + (T · P) : 24

gdzie P = F₂ - F₁.

6. Dodawanie wektorowe składowych półdobowych (SD).

Pływ półdobowy (R, r) w dowolnym czasie jest sumą pływu składowych M₂ i S₂. Tak więc:

R sin r = H · Ft sin (At + g) dla M₂ + H · Ft sin (At + g) dla S₂

R cos r = H · Ft cos (At + g) dlaM₂ + H · Ft cos (At + g) dla S₂

Z powyższych równań możemy obliczyć R i r. Używając kalkulatora z możliwością programowania, należy wykorzystać opcje zamiany współrzędnych biegunowych na prostokątne w celu uniknięcia dwuznaczności określenia znaku czy ćwiartki. Wykonując obliczenia „ręcznie” musimy mieć możliwość korzystania z funkcji trygonometrycznych, należy jednak zachować ostrożność dotyczącą wspomnianej dwuznaczności.

Poprawki płytkowodne

Faza pływu ćwierćdobowego ........... d₄ = 2r + f₄

Amplituda ....................................... D₄ = R2 · F₄

Poprawka wysokości pływu ....... h₄ = D₄ · cos d₄

Faza pływu 1/6 dobowego ............... d₆ = 3 r + f₆

Amplituda ........................................ D₆ = R3 · F₆

Poprawka wysokości pływu ........ h₆ = D₆ · cos d₆

Wartości h₄ i h₆ należy dodać algebraicznie do wypadkowego pływu półdobowego i dobowego w celu uzyskania wysokości dla żądanego czasu.

Uwagi dodatkowe przydatne w stosowaniu kalkulatorów programowalnych.

1. Jakkolwiek same pola tabel wskazują kolejność postępowania, to jednak nie zawsze będzie to optymalne rozwiązanie dla każdego kalkulatora.

2. W przypadku ograniczonych możliwości kalkulatora, często parametry mogą być łączone ze sobą i oddzielone znakiem dziesiętnym stosując odpowiedni mnożnik. Gdy g = 312° i H = 2,45 wprowadzić 312.245. Okazuje się, że w niektórych przypadkach postępując w ten sposób, nie tylko ograniczamy wielkość wymaganej pamięci kalkulatora, ale również ilość kroków programu.

3. Dysponując kalkulatorem o odpowiednich możliwościach, zaleca się:

a. Automatyczne wstawianie czasu, zarówno dla stałych jak i wybranych odstępów czasu.

b. Zapewnienie możliwości zmiany czasu rozpoczęcia serii przepowiedni.

c. Obliczanie przepowiedni dla kolejnych dni bez ponownego wprowadzania stałych harmonicznych dla każdego dnia.

d. Obliczanie przepowiedni dla drugiego portu w tym samym dniu bez konieczności ponownego wprowadzania danych astronomicznych (A i F).

e. Zapisywanie stałych harmonicznych dla dowolnego portu. W programie uwzględnić dodatkowe kroki umożliwiające wprowadzanie wartości sezonowych średniego poziomu i stałej harmonicznej. Jakkolwiek istnieje możliwość takiego zaprogramowania, aby obliczyć czas HW lub LW, to jednak okazuje się to mało pożyteczne. W wielu portach, dla których stosujemy tę metodę, krzywa pływu może być tak spłaszczona w tych punktach (HW lub LW), że rzeczywisty czas przepowiedni, który uzyskamy będzie praktycznie bezużyteczny. W portach, w których występują podwójne HW lub LW, bądź bezruch pływu, równie dobrze może wystąpić dwuznaczność dotycząca uzyskanego punktu na krzywej. W większości przypadków wskazane więc będzie wykreślenie odcinka krzywej na podstawie wyników kolejnych obliczeń.

4. W niektórych przypadkach lepiej będzie stosować centymetry aniżeli metry, zakładając, że nie występują poprawki płytkowodne.

Odpowiedź:

Wysokość pływu o godzinie 1330 wynosi 3,08 m. Zauważmy, że wprowadzając pewne uproszczenia w obliczeniach, otrzymano wyniki zbliżone - wariant a), b) i c).

1

---