Negacja (inaczej zaprzeczenie) to zdanie mające postać nieprawda, że p, gdzie p jest zdaniem. W rachunku zdań negacja zapisywana jest jako:
(lub
). Negację można zdefiniować ściślej jako jednoargumentowe działanie określone w zbiorze zdań, które każdemu zdaniu p przyporządkowuje zdanie nieprawda, że p. Negację zdania p uważa się za prawdziwą, gdy zdanie p jest fałszywe, zaś za fałszywą, gdy zdanie p jest prawdziwe.

Symbol negacji jako bramki logicznej:

Tablica prawdy (1 oznacza zdanie prawdziwe zaś 0 fałszywe):

p	¬ p
0	1
1	0

Złożenie dwóch negacji, daje w wyniku przekształcenie identycznościowe

Do oznaczenia negacji stosowana jest także angielska partykuła NOT

Koniunkcja to zdanie złożone mające postać p i q , gdzie p, q są zdaniami. W rachunku zdań koniunkcję zapisuje się symbolicznie jako:
. Przez koniunkcję rozumie się też zdanie mające postać p(1) i ... i p(n). Koniunkcję można zdefiniować precyzyjniej jako dwuargumentowe działanie określone w zbiorze zdań, które zdaniom p, q przyporządkowuje zdanie p i q

Działanie to pozostaje w ścisłym związku z działaniem przekroju zbiorów (patrz algebra zbiorów). Dlatego zdanie utworzone z innych zdań za pomocą koniunkcji jest też nazywane iloczynem logicznym. Koniunkcję zdań uznaje się za prawdziwą wtedy i tylko wtedy, gdy oba zdania p, q są prawdziwe.

Uproszczony schemat bramki logicznej AND - iloczynu bitowego

Symbol koniunkcji jako bramki logicznej:

Tablica prawdy (1 oznacza zdanie prawdziwe 0 zaś zdanie fałszywe):

0	0	0
0	1	0
1	0	0
1	1	1

Koniunkcja jest operacją dwuargumentową i charakteryzuje się następującymi cechami:

• przemienność

• łączność

Do oznaczenia koniunkcji stosowany jest także angielski spójnik AND (symbol funkcji boolowskiej).

• Koniunkcja zdań 2+2=4 i 3+1=5 jest fałszywa.

• Koniunkcja zdań 2+2=4 i 3+1=4 jest prawdziwa.

NAND (funktor Sheffera, kreska Sheffera, dysjunkcja) - dwuargumentowa funkcja boolowska (funktor logiczny) realizująca zaprzeczoną koniunkcję (NOT AND) - jest fałszywa wtedy i tylko wtedy, gdy oba składniki są prawdziwe. Często przedstawiana jest symbolicznie jako
, a w poręczniejszej notacji jako pionowa kreska "|", który oznacza logiczną negację koniunkcji dwóch argumentów. Jego znaczenie przedstawia poniższa tablica prawdy:

A	B	A NAND B
0	0	1
0	1	1
1	0	1
1	1	0

• Przy pomocy funktora NAND można zdefiniować wszystkie pozostałe funktory klasycznego rachunku zdań ((łac. p aut q). Jest to twierdzenie amerykańskiego logika polskiego pochodzenia Henry Sheffera, które opublikował w 1913 roku w artykule 'A Set of Five Independent Postulates for Boolean Algebras, with Application to Logical Constants'. Wcześniej na identyczny pomysł wpadł amerykański filozof Charles Peirce (artykuł 'A Boolean Algebra with One Constant' z 1880 roku), lecz jego pomysł nie został dostrzeżony.

• Inne funktory logiczne definiowane są w sposób następujący:

• 
  

• 
  

• 
  

• 
  

• Realizacją operacji NAND w elektronice jest bramka logiczna NAND. Oznaczana jest symbolem:

Alternatywa (suma logiczna) - w logice to:

1. Działanie dwuargumentowe określone w dowolnym zbiorze zdań bądź w zbiorze funkcji zdaniowych, które zdaniom (funkcjom zdaniowym) p i q przypisuje zdanie (funkcję zdaniową) prawdziwe wtedy i tylko wtedy gdy prawdziwe jest przynajmniej jedno ze zdań (funkcji) p i q

2. Dwuargumentowy spójnik zdaniowy, oznaczany
   (łac. p vel q) o znaczeniu odpowiadającemu wyżej zdefiniowanemu działaniu określonemu w zbiorze
   . Od poprzedniej definicji różni się tym, że jest definiowany na poziomie syntaktycznym, dzięki czemu unika się określania jego dziedziny.

3. Zdanie logiczne postaci
   , gdzie p i q są zdaniami.

Potoczne znaczenie słowa alternatywa jako dwóch wykluczających się możliwości odpowiada matematycznemu pojęciu alternatywy wykluczającej, a nie klasycznej alternatywy przedstawianej w tym artykule.

Uproszczony schemat bramki logicznej OR - sumy bitowej

Alternatywa pozostaje w ścisłym związku z dodawaniem zbiorów (patrz algebra zbiorów). Dlatego zdanie utworzone z innych zdań przy użyciu alternatywy jest też nazywane sumą logiczną. Alternatywa jest prawdziwa, jeżeli którekolwiek z jej zdań składowych jest prawdziwe. W przeciwnym razie alternatywa zdań jest fałszywa.

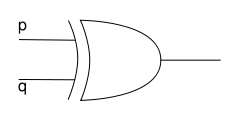
Symbol alternatywy jako bramki logicznej:

Tablica prawdy dla alternatywy (0 oznacza zdanie fałszywe, 1 - zdanie prawdziwe):

p	q	p ∨ q
0	0	0
0	1	1
1	0	1
1	1	1

Alternatywa jest:

• przemienna

• łączna

W językach programowania dla oznaczenia alternatywy używany jest często angielski spójnik OR. W języku C/C++ i pochodnych oznacza się ją przez " | | ".

NOR (funktor Pierce'a, binegacja) - dwuargumentowa funkcja boolowska (funktor logiczny) realizująca zaprzeczoną sumę logiczną (NOT OR) - jest prawdziwa wtedy i tylko wtedy, gdy oba składniki są fałszywe. Często przedstawiana pionowa kreska "|" przechodząca przez symbol alternatywy "v" dwóch argumentów, co oznacza jej logiczną negację. Jego znaczenie przedstawia poniższa tablica prawdy:

A	B	A nor B
0	0	1
0	1	0
1	0	0
1	1	0

NOR jest równoważna negacji sumy logicznej

a NOR b = NOT (a OR b)

NOR jest również równoważna iloczynowi negacji logicznych

a NOR b = (NOT a) AND (NOT b)

Symbol zaprzeczenia alternatywy jako bramki logicznej:

Za pomocą funkcji NOR możemy zdefiniować negację:

NOT a = a NOR a

alternatywę:

a OR b = NOT ( a NOR b) = ( a NOR b) NOR ( a NOR b )

koniunkcję:

a AND b = NOT (( NOT a ) OR ( NOT b )) = ( NOT a ) NOR ( NOT b ) = ( a NOR a ) NOR ( b NOR b )

czyli dowolną funkcję logiczną. Dlatego też ta funkcja jest ważna (podobnie jak NAND).

Alternatywa wykluczająca (alternatywa rozłączna, różnica symetryczna, suma modulo 2, kontrawalencja, XOR, exclusive or, EOR) to logiczny funktor zdaniotwórczy (dwuargumentowa funkcja boolowska) . Różnica symetryczna zdań
jest prawdziwa wtedy i tylko wtedy, gdy dokładnie jedno ze zdań p,q jest prawdziwe:

Innym oznaczeniem jest
.

Tablica prawdy alternatywy wykluczającej:

p	q
0	0	0
0	1	1
1	0	1
1	1	0

Przy użyciu funkcji XOR dla więcej niż dwóch argumentów wynik jest prawdziwy gdy nieparzysta liczba argumentów jest prawdą.

Informatyka

W informatyce operację alternatywy wykluczającej stosuje się do par liczb naturalnych wykonując operacje na cyfrach zapisów binarnych tych liczb. Jest to zwykła logiczna alternatywa wykluczająca rozszerzona na ciągi bitów. Wykonuje się ją bit po bicie. Np.:

7 ^ 5 =      (w językach C/C++ alternatywę wykluczającą oznaczamy za pomocą symbolu ^)

= 0000111₂ ^ 0000101₂ =   (liczby w systemie binarnym)

= 0000010₂ =    (efekt operacji na kolejnych cyfrach)

= 2     (wynik w postaci dziesiętnej)

Własności [edytuj]

• Operacja XOR jest przemienna:

• Operacja XOR jest łączna:

• Istnieje element neutralny; jest nim 0:

• Dla każdego elementu istnieje element odwrotny; jest nim ten sam element:

• 
  

Oznacza to, że alternatywa wykluczająca jako działanie dwuargumentowe zadaje na zbiorze w którym jest określona, strukturę grupy abelowej.

Ponadto:

• Niech
  . Wówczas operacja
  wprowadza na zbiorze A metrykę^[1]

Bramka XNOR - bramka logiczna realizująca funkcję negacji alternatywy wykluczającej (tzw. Bramka Równoważności).

Bramka ta neguje wynik bramki XOR czyli zwraca fałsz (0), jeśli dokładnie jedno z wejść: A lub B jest prawdą (1), a w przeciwnym wypadku zwraca prawdę. Innymi słowy bramka XNOR dopuszcza pojawienie się dwóch takich samych sygnałów na wejściu.

Tablica prawdy XNOR
A	B	Q
0	0	1
0	1	0
1	0	0
1	1	1

Bramka trójstanowa, bramka TS (ang. three-state) - jest to bramka logiczna, która na wyjściu, oprócz dwóch stanów logicznych (0 i 1 logicznej), może przyjmować stan logicznie nieokreślony. Stan ten nazywany jest stanem wysokiej impedancji i oznaczany jest (Z).

Bramki TS [edytuj]

Bramki trójstanowe, oprócz standardowych wejść, posiadają również wejście dodatkowe S.

Wyróżniamy bramki:

NAND TS [edytuj]

Kiedy wejście S przyjmuje wartość 1 logicznej, bramka NAND TS działa jak zwykła bramka NAND. Natomiast kiedy na wejściu S pojawia się 0 logiczne, na wyjściu bramki jest stan wysokiej impedancji.

S	a	b	y
0	0	0	(Z)
0	0	1	(Z)
0	1	0	(Z)
0	1	1	(Z)
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	0

NOT TS [edytuj]

Bramka NOT TS nazywana jest również negatorem trójstanowym.

W bramce NOT TS wejście S jest zanegowane, więc pracuje ona tak jak zwykły negator dla S=0. Natomiast dla S=1, na wyjściu negatora trójstanowego jest stan wysokiej impedancji.

S	a	y
0	0	1
0	1	0
1	0	(Z)
1	1	(Z)

1

---