nr ćwicz	data	Dominik Witaszek	Wydział Elektryczny	Semestr II	grupa E8
201	21.03.2011
			przygotowanie	wykonanie	ocena ostatecz.
Prowadzący: dr Magdalena Elantkowska

Wyznaczanie zależności przewodnictwa od temperatury

dla przewodników i półprzewodników

Teoria:

Prawo Ohma w najogólniejszej postaci stwierdza, że gęstość prądu w dowolnym miejscu materiału przewodzącego jest wprost proporcjonalna do natężenia pola elektrycznego.

J=σE

W powyższym równaniu J oznacza gęstość prądu (stosunek prądu do powierzchni przekroju), natomiast E natężenie pola elektrycznego. Współczynnik proporcjonalności nazywamy przewodnictwem elektrycznym. Wartość przewodnictwa określona jest bezpośrednio przez koncentrację i ruchliwość nośników ładunku

σe(n_n + p_p)

Koncentrację elektronów n i dziur p określamy jako ilość tych nośników w jednostce objętości, a ruchliwość (elektronów - _e dziur - _p) jest stosunkiem prędkości unoszenia do natężenia pola elektrycznego.

W półprzewodnikach zarówno koncentracja, jak i ruchliwość zależą od rodzaju materiału i od temperatury, więc przewodnictwo również zależy od tych parametrów.

W przewodnikach (metalach) koncentracja nośników jest bardzo duża i nie zależy od temperatury. O zależności temperaturowej przewodnictwa decyduje zmniejszanie się ruchliwości ze wzrostem temperatury. Zależność tę wyraża się przez opór i ma ona postać

R=R₀[1+(T-T₀)]

gdzie R₀ jest oporem w temperaturze T₀, a ?- średnim współczynnikiem temperaturowym oporu.

Powyższy wzór jest słuszny dla niezbyt dużego przedziału temperatur. W różnych przedziałach współczynnik  przybiera różne wartości.

Dla półprzewodników ilość elektronów przechodzących na inny poziom energetyczny zależy wykładniczo od różnicy poziomów oraz od temperatury i wyraża się w przypadku półprzewodników samoistnych wzorem

w którym : E_g - szerokość pasma zabronionego, k - stała Boltzmanna.

Ze względu na to, że każdemu elektronowi w paśmie przewodnictwa odpowiada jedna dziura w paśmie walencyjnym, koncentracje obu rodzajów nośników są takie same.

W przypadku półprzewodników domieszkowanych koncentracje nośników są określone przez

odległości energetyczne E_d oraz E_a oraz przez temperaturę

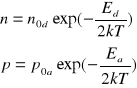
Gdy wzrasta temperatura ilość nośników pochodzących z poziomów domieszkowych również rośnie,

aż do chwili, gdy wszystkie elektrony opuszczą poziomy donorowe lub zapełnią poziomy akceptorowe. Dalsze podwyższanie temperatury nie prowadzi do wzrostu koncentracji (nasycenie domieszkowe -

- patrz rys.1). Dopiero przy większym wzroście temperatury zaczynają przeważać nośniki samoistne i koncentracja zaczyna szybko wzrastać.

Temperaturową zależność przewodnictwa możemy wyrazić w postaci:

[Author ID0: at Thu Nov 30 00:00:00 1899 ]

przez E_dom rozumiemy jedną z wielkości E_d lub E_a , zależnie od rodzaju półprzewodnika.

W odpowiednio niskich temperaturach można zaniedbać pierwszy składnik powyższego wzoru,

natomiast w wysokich, gdy nastąpi nasycenie poziomów domieszkowych, można zaniedbać składnik drugi.

W pierwszym przypadku przewodnictwo będzie wynosić

w drugim zaś

Zależność temperaturową przewodnictwa półprzewodnika najdogodniej analizować za pomocą wykresu w skali półlogarytmicznej. Logarytmując powyższy wzór otrzymamy wyrażenie postaci

Rys.1. Logarytm przewodnictwa w funkcji odwrotności temperatury.

Zasada pomiaru:

W celu wyznaczenia szukanych zależności dokonujemy pomiarów oporu elektrycznego przewodnika drutowego i półprzewodnika w różnych temperaturach. Badane materiały umieszczamy w ultratermostacie i mierzymy ich opory za pomocą mostka Wheatstone'a.

Budowę mostka Wheatstone'a przedstawia rys. 6.32. Główną czynnością przy posługiwaniu się mostkiem Wheatstone'a jest dobranie oporu R (składa się on z szeregu oporników w układzie dekadowym) w ten sposób, aby uzyskać równowa­gę mostka polegającą na zerowaniu się prądu płynącego przez galwanometr G.

Warunkiem równowagi jest równość potencjałów elektrycznych w punktach B i D.

Dla ułatwienia pomiaru wskazana jest znajomość przybliżonej wartości oporu mierzonego, którą znajdujemy za pomocą omomierza. Wartość oporu R\ dobie­ramy w ten sposób, aby była tego samego rzędu co opór Rx.

Następnie włączamy obwód baterii oraz przycisk O, l G i pokrętłami oporów dekadowych, rozpoczynając od największych, doprowadzamy do zerowego wy­chylenia galwanometru. Przycisk O, l G włącza galwanometr przez opór zabezpie­czający R: zmniejszający czułość galwanometru. W celu dokładniejszego zrów­noważenia mostka wciskamy z kolei przycisk G i powtarzamy czynności związane z osiągnięciem zerowego wychylenia, nie zmieniając największej dekady. Po uzy­skaniu równowagi wyłączamy źródło prądu i kontrolujemy wskazanie zerowe galwanometru.

Przebieg ćwiczenia

1. Włączyć do sieci ultratermostat, dołączyć baterie, galwometr i badane oporniki do mostka Wheatstone'a.

2. Ustalić w ultratermostacie temp. Około 20⁰C

3. Zmierzyć opór przewodnika i półprzewodnika.

4. Zmieniać tem. co około 5⁰C w zakresie 20-90⁰C i mierzyć opory.

5. Wykreślić zależność R=f(T) na wspólnym wykresie dla przewodnika i półprzewodnika. W razie potrzeby zastosować różne skale dla każdego opornika.

6. Dla półprzewodników obliczyć ln(1/R) oraz 1/T i sporządzić wykres zależności tych wielkości. Temperatura musi być wyrażona w kelwinach.

7. Za pomocą regresji liniowej obliczyć współczynnik nachylenia oraz jego błąd.

8. Wyznaczyć energię poziomu domieszkowego. Energie wyrazić w dżulach i elektronowoltach.

9. Obliczyć E_dom metodą różniczki zuperłnej.

10. Zaokrąglić obliczone wartości i przedstawić ostateczną postać wyniku.

Pomiary

Temperatura ^0C	Przewodnik [ Ω ]	Półprzewodnik [kΩ]
23,1	110	276
26,5	111	238
32	119	168
37	121	128
43	124	101
48,3	126	80
54	129	65
59,6	131	52
64,6	134	43
69	135	37
74,8	138	30

Półprzewodnik:

L.p.	T [K]	1/T [1/K]	R [Ω]	Ln(1/R)
1	296,25	0,00338	276000	-12,528
2	299,65	0,00334	238000	-12,380
3	305,15	0,00328	168000	-12,032
4	310,15	0,00322	128000	-11,760
5	316,15	0,00316	101000	-11,523
6	321,45	0,00311	80000	-11,290
7	327,15	0,00306	65000	-11,082
8	332,75	0,00301	52000	-10,859
9	337,75	0,00296	43000	-10,669
10	342,15	0,00292	37000	-10,519
11	347,95	0,00287	30000	-10,309

Współczynnik nachylenia prostej ln(1/R)=f(1/T) obliczony metodą regresji wynosi :

a≈ -4362,68

Δa≈ 63,56

Poziom domieszkowy będzie zatem równy :

a=-E_dom/2k

E_dom=-2ak=-2*(-4362,68)*1,38*10^-23=12040,9968*10^-23=1,20409968*10^-19≈1,20*10^-19[J]

E_dom=1,20409968*10^-19*0,62415 · 10¹⁹=0,75153882 ≈0,75 [eV]

Błąd wyznaczenia poziomu domieszkowego :

ΔE=Δa*2*k=63,5539*2*1,38*10^-23=1,7540876*10^-21≈1,75*10^-21 [J]

ΔE=175,40876*10^-23*0,62415*10^19=109,48138*10^-4=0,010948138 ≈0,02 [eV]

Wnioski

Celem ćwiczenia było wyznaczenie zależności przewodnictwa od temperatury dla półprzewodników i przewodników. Zależność tę przedstawia wykres, który został wykonany w pierwszej części protokołu. Następnie wyznaczyliśmy poziom energii domieszkowania, którego wartość została przedstawiona na końcu obliczeń..

Z załączonego wykresu można zauważyć, że badany półprzewodnik charakteryzuje się dużym spadkiem oporności wraz z temperaturą. Sugeruje to, że badany termistor był typu NTC (Negative Temperature Ceofficient). Natomiast przewodnik charakteryzuje się wzrostem opornosći wraz z temperturą. Błędy pomiaru wynikają głównie z trudności w utrzymaniu jednakowej temperatury podczas przeprowadzania długotrwałego pomiaru oporności za pomocą mostka Wheatstone'a.

4

---