Wykład 3.

Funkcja produkcji

1. Interpretacja ekonomiczna parametrów funkcji produkcji

Cobb - Douglasa.

Pomiary zależności, jakie występują pomiędzy nakładami pracy żywej i zasobami środków trwałych a ilością otrzymanego produktu to jeden z podstawowych problemów ekonometrycznej analizy procesów produkcyjnych. Pierwszymi którzy tą kwestią zajęli się byli C.W.Cobb i P.H.Douglas. Stworzona przez nich funkcja produkcji posiada wiele zalet i dotychczas jest stosowana z dużym powodzeniem w wielu analizach ekonomicznych.

Funkcja produkcji typu Cobb-Douglasa ma postać:

/ 1 /

przy czym:

wartość (ilość) produkcji

różne rodzaje nakładów pracy żywej i majątku

stałe parametry o dodatnich wartościach

Poszczególnym parametrem funkcji typu Cobb-Douglasa można nadać ciekawą interpretację ekonomiczną :

W tym celu udowodnimy dwa twierdzenia:

Twierdzenie 1.

Elastyczność wielkości produkcji względem wielkości nakładów (zasobów) X_i w przypadku funkcji produkcji danej wzorem (1 ) jest równa α_i .

Elastyczność wielkości produkcji względem wielkości nakładów to inaczej

relacja względnych zmian wielkości produkcji do względnych zmian wielkości

nakładów, czyli :

=

=

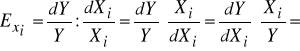
Oszacowana wartość parametrów α_i
mówi, że jeżeli wartość zmiennej
wzrośnie o 1% to wartość (ilość) produkcji (Y) wzrośnie o
%.

Trzeba jednak podkreślić, że oszacowane wyniki należy interpretować ostrożnie, gdyż definicja elastyczności zakłada nieskończenie mały przyrost wartości zmiennej objaśniającej, a w praktyce interesują nas przyrost rzędu 1%, 2%, a nawet 5%, a więc względnie duże². Należy się zatem spodziewać, że wyniki będą przybliżone i to tym bardziej, im większy przyrost zmiennej objaśniającej będziemy zakładali. Dodatkowo w definicji elastyczności zakłada się zmianę jednej zmiennej przy stałości pozostałych a takie autonomiczne zmiany czynników produkcji rzadko są możliwe. W przypadku modelu potęgowego, a takim jest funkcja produkcji Cobb - Douglasa, możemy jednak dokładnie obliczyć zarówno przyrosty bezwzględne, jak i względne przy dowolnych a nawet jednoczesnych względnych zmianach wartości zmiennych objaśniających. Załóżmy, że analizujemy dwuczynnikową funkcję produkcji Cobb - Douglasa postaci :

/ 2 /

przy czym względne zmiany kapitału i pracy wynoszą odpowiednio :
i
to względna zmiana zmiennej
wyniesie
:

Oznaczmy :

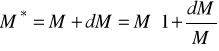
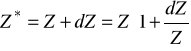
Stąd :

dokonując podstawienia :

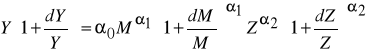
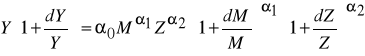
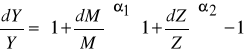
/ 3 /

Jeżeli zmiany chcemy wyrazić w procentach powyższe równanie należy dwustronnie przemnożyć przez 100%

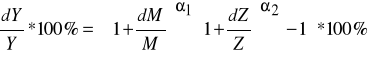
/ 4 /

Jeżeli założymy, że np. tylko zmieni się kapitał natomiast zatrudnienie nie ulegnie zmianie to procentowe zmiany produkcji można obliczyć :

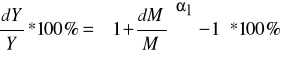
Jeżeli to będzie wzrost kapitału o 1% wtedy :

Twierdzenie 2.

Jeżeli funkcja produkcji ma postać (1) i jeżeli nakłady (zasoby) wszystkich czynników produkcji wzrastają o p procent w porównaniu ze stanem wyjściowym to produkcja wzrasta:

a) w tempie wolniejszym niż nakłady, jeżeli suma oszacowań parametrów

α₁ + α₂ +...+ α_k < 1

2. w tym samym tempie co nakłady, jeżeli suma oszacowań parametrów

α₁ + α₂ + ...+ α_k = 1

3. w tempie szybszym niż nakłady, jeżeli suma oszacowań parametrów

α₁ + α₂ +... α_k > 1

Aby udowodnić to twierdzenie, weźmy najpierw funkcję (1 ) i obliczmy, jaki będzie poziom produkcji Y^* odpowiadający nakładom zwiększonym o p procent w porównaniu ze stanem wyjściowym.

Mamy wtedy:

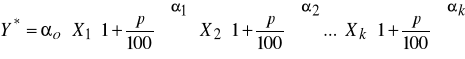
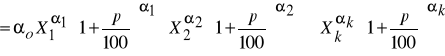
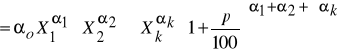
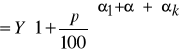
stąd:

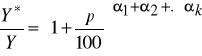
Zauważmy teraz, że ułamek
zgodnie z założeniem, jest stosunkiem wielkości produkcji przy nakładach (zasobach) zwiększonych o
% do wielkości produkcji w sytuacji wyjściowej, gdy nakłady (zasoby) wynosiły
, tak więc ułamek ten jest indeksem produkcji.

Jeżeli teraz oszacowania sumy parametrów α₁+α₂+...α_k < 1, to oczywiście:

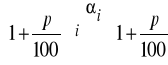
, co dowodzi prawdziwości punktu a) tezy twierdzenia.

Punkty b) i c) udowadnia się w podobny sposób.

Milczącym założeniem, jakie zwykle czyni się przy posługiwaniu się funkcją produkcji typu Cobb-Douglasa, jest to, że poszczególne rodzaje nakładów (zasobów) mogą się przynajmniej w pewnych granicach zastępować. Tę zastępowalność, czyli substytucję nakładów, należy rozumieć w ten sposób, że tę samą ilość produkcji można otrzymać stosując poszczególne czynniki produkcji w różnych proporcjach. Najbardziej typowe zagadnienie to zastępowanie pracy żywej przez majątek trwały (produkcyjny).

Zjawisko substytucji można analizować za pomocą współczynników elastyczności stopy substytucji postaci:

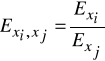
/ 4 /

gdzie:

- elastyczność stopy substytucji zmiennej
przez zmienna

- elastyczności zmiennych
względem zmiennej objaśnianej.

W przypadku funkcji produkcji typu Cobb-Douglasa elastyczność substytucji jest stała i wyraża się wzorem :

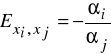
/ 5 /

przy czym znak wskazuje na kierunek substytucji.

Wartość współczynnika
informuje o ile procent powinna wzrosnąć wartość zmiennej
_, aby przy spadku wartości zmiennej
o 1% wartość produkcji utrzymała się na niezmienionym poziomie.

W przypadku dwuczynnikowej funkcji produkcji typu Cobb - Douglasa :

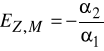
Podobnie jak w przypadku elastyczności zależność powyższa jest prawdziwa w przypadku bardzo niewielkich zmian wartości kapitału i zatrudnienia. Jeżeli zmiany te są większe należy korzystać z obliczeń dokładnych. Korzystając ze wzoru / 3 / mamy :

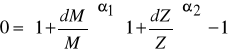
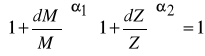
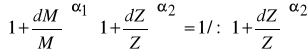
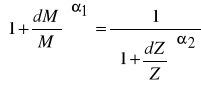
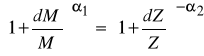
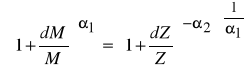
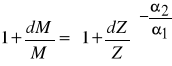
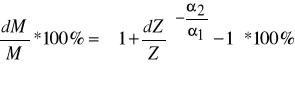
Z problematyką substytucji nakładów związane jest ściśle pojęcie izokwanty produkcji. Jeżeli zgodnie ze wzorem (1) założymy, że można wyróżnić k rodzajów nakładów, to izokwanta produkcji będzie zbiorem tych wszystkich punktów

k-wymiarowej przestrzeni o współrzędnych
dla których wartość

produkcji jest stała i równa z góry danej liczbie
. Inaczej mówiąc, izokwanta

produkcji jest tworem geometrycznym o takiej własności, że kombinacja

nakładów (zasobów), odpowiadająca punktom leżącym na izokwancie, daje tę

samą wielkość produkcji.

Funkcja produkcji typu Cobb-Douglasa pozwala również mierzyć efekty postępu technicznego i organizacyjnego w procesach produkcyjnych.

Aby mierzyć efekt postępu technicznego i organizacyjnego należy wprowadzić po prawej stronie funkcji Cobb-Douglasa czynnik o postaci gdzie γ jest stałym parametrem.

Po tej modyfikacji funkcja produkcji przybiera postać:

/ 6 /

Jeżeli teraz przeanalizujemy wielkość produkcji w okresie t i okresie t +1, przy założeniu, że w obu okresach stosowano te same ilości czynników produkcji
to łatwo sprawdzić, że indeks produkcji roku t + 1 do roku t jest równy:

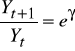
/ 7 /

Wartość tego indeksu zależy od wartości parametru γ i jest większa, równa lub mniejsza od jedności w zależności od tego czy γ > 0, γ = 0, γ < 0

Twierdzenie 3.

Parametr funkcji produkcji / 6 / jest miernikiem efektów postępu technicznego i organizacyjnego. Jeżeli γ > 0 to istnieją dodatnie efekty postępu technicznego i organizacyjnego, tak że produkcja dzięki nim wzrasta średnio o
procent w skali rocznej. Jeżeli γ = 0 to nie występuje postęp techniczny i organizacyjny. W przypadku γ < 0 występuje regres techniczny i organizacyjny wyrażający się tym, że przy stałych nakładach produkcja maleje średnio o
procent w skali rocznej.

2. Funkcja produkcji o stałej elastyczności substytucji.

Funkcja typu Cobb - Douglasa nie jest jedyną funkcją produkcji zakładającą możliwość substytucji czynników produkcji. W literaturze ekonometrycznej opisano wiele takich funkcji. Jedną z bardziej znanych jest funkcja produkcji o stałej elastyczności substytucji CES ( Constant Elasticity of Substitution )³. Funkcję tę nazywa się też niekiedy SMAC⁴. Funkcja ta dla dwóch czynników produkcji ma postać :

/ 8 /

gdzie :

wielkość produkcji,

nakłady pracy ( np. zatrudnienie ),

nakłady kapitałowe ( np. majątek produkcyjny ),

są stałymi parametrami, przy czym
ma analogiczne znaczenie

jak suma
w przypadku funkcji produkcji

Cobb - Douglasa.

W przypadku rozpatrywania nie dwóch lecz k>2 czynników :
decydujących o poziomie produkcji stosuje się następujące uogólnienie :

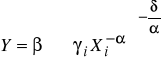
/ 9 /

przy czym
sumują się do jedności.

Estymacja parametrów funkcji / 8 / oraz / 9 / jest w praktyce trudna, gdyż funkcji tych nie można bezpośrednio sprowadzić do postaci liniowej względem nieznanych parametrów. Pewne propozycje poczynił w tym zakresie J. Kmenta⁵.

Aproksymację funkcji SMAC (CES) uzyskuje się dzięki rozwinięciu postaci / 8 /

( po obustronnym zlogarytmowaniu ) w szereg Taylora wokół
:

Z. Pawłowski, Ekonometria, PWE, Warszawa 1980.

² Istnieje jeszcze jeden powód ostrożności : w rzeczywistości nie znamy prawdziwej wartości elastyczności a dysponujemy jedynie jej oszacowaniem, z natury rzeczy obarczonym błędem.

³ Nazwę tę wprowadzili jej odkrywcy T. M. Brown oraz P. de Cani : Technological Change in the United States 1950 - 1960, Productivity Measurement Review, 1962.

⁴ Z kolei ta nazwa pochodzi od nazwisk innego zespołu, którzy niezależnie od Browna i de Cani odkryli tę funkcję: R. A. Solow, B. S. Minhas, K. J. Arrow, H. B. Chenery, Capital - Labor Substitution and Economic Efficiency, Review of Economics and Statistics, 1961.

⁵ J. Kmenta, Some properties of alternative estimates of the Cobb - Douglas production function, Econometrica, 1964.

68

72

68

---