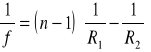
![]()
(1)
nr ćwicz. 303 |
data 3.03 2008 |
Sylwia Kożykowska |
Wydział Fizyki Technicznej |
Semestr II |
grupa 1 nr lab. 1 |
prowadzący dr K. Łapsa
|
przygotowanie |
wykonanie |
ocena ostateczna |
||
Wyznaczanie ogniskowych soczewek ze wzoru soczewkowego oraz metodą Bessela.
Podstawy teoretyczne
Soczewką nazywamy ciało przezroczyste ograniczone dwoma powierzchniami sferycznymi. Oś łączącą środki krzywizny obu powierzchni nazywamy osią optyczną soczewki. Światło przechodzące przez soczewkę ulega kolejno załamaniu na obu jej powierzchniach. Promień przechodzący przez środek optyczny soczewki nie ulega załamaniu niezależnie od kąta padania na soczewkę. Wiązka promieni biegnąca równolegle do do osi optycznej skupia się w jednym punkcie, zwanym ogniskiem. Odległość ogniska od środka soczewki nazywamy ogniskową.
Dobierając odpowiednio promienie krzywizn buduje się soczewki skupiające i rozpraszające. Wiązka równoległa, padająca na soczewkę rozpraszającą staje się po przejściu przez nią wiązką rozbieżną. W tym przypadku ogniskiem jest punkt przecięcia się przedłużeń promieni załamanych.
Położenie ogniska zależne jest od współczynnika załamania n materiału soczewki względem ośrodka, w którym się znajduje, oraz od promieni krzywizn obu powierzchni ograniczających R1 i R2. Zależność ogniskowej f od powyższych parametrów określona jest równaniem:
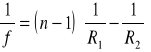
![]()
(1)
Soczewki mają zdolność odwzorowywania punktów polegającą na tym, że promienie wybiegające z punktu P, zwanego przedmiotem, zostają skupione po przejściu przez soczewkę w punkcie O tworząc obraz przedmiotu. Położenie obrazu zależy od położenia przedmiotu oraz od ogniskowej soczewki - określone jest tzw. równaniem soczewkowym:
![]()
, (2)
gdzie: p - odległość przedmiotu od soczewki,
o - odległość obrazu od soczewki.
Równanie (2) może być stosowane w przypadkach, gdy:
(a) promienie wybiegające z P tworzą niewielki kąt z osią optyczną;
(b) soczewka jest cienka, tzn jej grubość jest mała w porównaniu z promieniami krzywizny.
W stosunku do odległości p, o, R1, R2 oraz f istnieje umowa określająca ich znaki:
(a) p jest zawsze dodatnie,
(b) o, R, f są dodatnie, gdy leżą po przeciwnej stronie soczewki niż przedmiot,
(c) o, R i f są ujemne, gdy leżą po tej samej stronie co przedmiot.
Metody znajdowania ogniskowych.
Na podstawie wzoru soczewkowego. Odległości p i o występujące we wzorze (2) są łatwo mierzalne, dzięki czemu wzór ten możemy wykorzystać do wyznaczenia ogniskowej f. Na ławie optycznej umieszczamy świecący przedmiot, soczewkę oraz ekran w ten sposób, aby na ekranie otrzymać wyraźny obraz przedmiotu. Ekran i soczewka umieszczone są na wózkach, co umożliwia ich przesuwanie wzdłuż ławy. Wskaźnik wózka przesuwający się względem podziałki naniesionej na ławie wyznacza dokładnie położenie wózka lub soczewki.
Ponieważ oszacowanie ostrości obrazu jest połączone z dużą niepewnością, ustawienie wózka powtarzamy kilkakrotnie, notujemy za każdym razem położenie wózka, po czym obliczamy wartość średnią.
Znając odpowiednie położenia obliczamy odległości przedmiotu i obrazu, a następnie z równania (2) znajdujemy ogniskową.
Opisana metoda nie może być stosowana bezpośrednio do soczewek rozpraszających, gdyż nie dają one obrazu rzeczywistego. Możemy jednak obliczyć ogniskową układu złożonego z badanej soczewki rozpraszającej i soczewki skupiającej. Mając ogniskową układu f oraz ogniskową fs soczewki skupiającej oraz znajdujemy ogniskową fr soczewki rozpraszającej z równania:
![]()
(3).
d- wzajemna odległość ogniskowych fs , fr
Przy stosowaniu tej metody należy pamiętać, że obraz rzeczywisty uzyskamy wtedy, gdy spełniony będzie warunek ![]()
oraz, że ogniskowa soczewki rozpraszającej jest ujemna.
metoda bessela. Odległości obrazu i przedmiotu występują w równaniu (2) w postaci symetrycznej, tzn. że po zamianie ich wartości równanie pozostaje w dalszym ciągu prawdziwe. Fizyczną konsekwencją symetrii równania soczewkowego jest możliwość uzyskania ostrego obrazu przy dwóch położeniach soczewki względem przedmiotu.
Przy stałej odległości l przedmiotu od ekranu obraz powstaje w odległości o oraz o' = p od soczewki (rysunek). Przy jednym położeniu obraz jest pomniejszony, a przy drugim powiększony w stosunku do przedmiotu.
Na podstawie rysunku możemy napisać układ równań
o + p = l
o - p = e.
Z powyższych równań wyliczamy p oraz o i następnie wstawiamy do równania (2), otrzymując po prostych przekształceniach
![]()
(4).
Aby wyznaczyć ogniskową soczewki lub układu soczewek z równania (4) należy zmierzyć odległość przedmiotu od ekranu l oraz odległość e między dwoma położeniami soczewki, przy których obraz na ekranie jest ostry.
A,C - soczewki skupiające - ogniskowe wyznaczamy bezpośrednio ze wzoru (2)
4,6 - soczewki rozpraszające - stosujemy metodę układu soczewek, ogniskową wyznaczamy ze wzoru (3)
Błędy zachodzące przy wyznaczaniu ogniskowych soczewek :
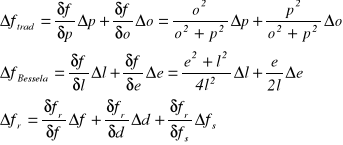
![]()
- błąd ogniskowej układu soczewek wyznaczonej metodą Bessela lub z wzoru soczewkowego;
![]()
- błąd wyznaczenia ogniskowej soczewki skupiającej wchodzącej w skład układu soczewek;
![]()
- błąd pomiaru odległości pomiędzy soczewkami;
![]()
SOCZEWKA C
p [m] |
o [m] |
l [m] |
e [m] |
[m] |
[m] |
[m] |
[m] |
0,3315 |
0,6585 |
0,99 |
0,3155 |
0,002820 |
0,220498 |
0,000435 |
0,222364 |
0,3630 |
0,6270 |
|
0,2770 |
0,003259 |
0,229900 |
0,000409 |
0,228124 |
0,3550 |
0,6350 |
|
0,2740 |
0,003143 |
0,227702 |
0,000408 |
0,228541 |
0,3440 |
0,6460 |
|
0,3100 |
0,002988 |
0,224469 |
0,000431 |
0,223232 |
0,3530 |
0,6370 |
|
0,2990 |
0,003114 |
0,227132 |
0,000424 |
0,224924 |
0,3580 |
0,6320 |
|
0,2950 |
0,003186 |
0,228541 |
0,000421 |
0,225524 |
Obliczam przedział, w którym znajduje się ogniskowa soczewki z prawdopodobieństwem 68,3%:
Wartość średnia ![]()
=0,226374m , a odchylenie standardowe ![]()
=0,003395m.
Wartość średnia ![]()
=0,225452m , a odchylenie standardowe ![]()
=0,002507m.
Po wymnożeniu przez współczynnik Studenta-Fishera, (który dla n=6 pomiarów wynosi 1,2),
![]()
=0,004074m oraz ![]()
=0,0030084m.
Ogniskowa wynosi:
![]()
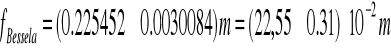
Z prawdopodobieństwem 99,7% ogniskowa soczewki znajduje się w przedziale:
![]()
=0,010185m, po wymnożeniu przez współczynnik studenta-Fishera ![]()
=0,012222m
![]()
=0,007521m, po wymnożeniu przez współczynnik studenta-Fishera ![]()
=0,0090252m
Ogniskowa wynosi:
![]()
![]()
SOCZEWKA A
p [m] |
o [m] |
l [m] |
e [m] |
[m] |
[m] |
[m] |
[m] |
0,1230 |
0,8670 |
0,99 |
0,7590 |
0,001178 |
0,107718 |
0,000780 |
0,102025 |
0,1270 |
0,8630 |
|
0,7560 |
0,001191 |
0,110708 |
0,000778 |
0,103173 |
0,1260 |
0,8640 |
|
0,7565 |
0,001187 |
0,109964 |
0,000778 |
0,102982 |
0,1270 |
0,8630 |
|
0,7555 |
0,001191 |
0,110708 |
0,000777 |
0,103364 |
Obliczam przedział, w którym znajduje się ogniskowa soczewki z prawdopodobieństwem 68,3%:
Wartość średnia ![]()
=0,109774m , a odchylenie standardowe ![]()
=0,001415m.
Wartość średnia ![]()
=0,102886m , a odchylenie standardowe ![]()
=0,000595m.
Po wymnożeniu przez współczynnik Studenta-Fishera, (który dla n=4 pomiarów wynosi 1,3),
![]()
=0,0018395m oraz ![]()
=0,0007735m
Ogniskowa wynosi:
![]()
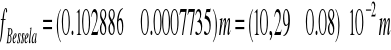
Z prawdopodobieństwem 99,7% ogniskowa soczewki znajduje się w przedziale:
![]()
=0,004245m, po wymnożeniu przez współczynnik studenta-Fishera ![]()
=0,0055185m
![]()
=0,001785m, po wymnożeniu przez współczynnik studenta-Fishera ![]()
=0,0023205m
Ogniskowa wynosi:
![]()
![]()
Ze wzoru (3) wyznaczamy ogniskową soczewki rozpraszającej:
![]()
Odległość między soczewkami: d=0,023m
SOCZEWKA A+4
p [m] |
o [m] |
l [m] |
e [m] |
[m] |
[m] |
[m] |
[m] |
0,150 |
0,840 |
0,99 |
0,725 |
0,001278 |
0,127273 |
0,000750 |
0,114766 |
0,153 |
0,837 |
|
0,721 |
0,001291 |
0,129355 |
0,000747 |
0,116227 |
0,155 |
0,835 |
|
0,719 |
0,001300 |
0,130732 |
0,000745 |
0,116954 |
0,153 |
0,837 |
|
0,720 |
0,001291 |
0,129355 |
0,000746 |
0,116591 |
0,149 |
0,841 |
|
0,724 |
0,001274 |
0,126575 |
0,000749 |
0,115132 |
Obliczam przedział, w którym znajduje się ogniskowa soczewki z prawdopodobieństwem 68,3%:
Wartość średnia ![]()
=0,128658m , a odchylenie standardowe ![]()
=0,001698m.
Wartość średnia ![]()
=0,115934m , a odchylenie standardowe ![]()
=0,000943972m.
Po wymnożeniu przez współczynnik Studenta-Fishera, (który dla n=4 pomiarów wynosi 1,3),
![]()
=0,0022074m oraz ![]()
=0,0012271636m.
Ogniskowa wynosi:
![]()
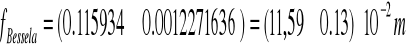
Z prawdopodobieństwem 99,7% ogniskowa soczewki znajduje się w przedziale:
![]()
=0,005094m, po wymnożeniu przez współczynnik studenta-Fishera ![]()
=0,0066222m
![]()
=0,028319m, po wymnożeniu przez współczynnik studenta-Fishera ![]()
=0,0368149m
Ogniskowa wynosi:
![]()
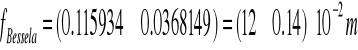
SOCZEWKA 4
[m] |
[m] |
d [m] |
[m] |
0,127273 |
0,107718 |
0,023 |
-0,55138 |
0,129355 |
0,110708 |
|
-0,60843 |
0,130732 |
0,109964 |
|
-0,54743 |
0,129355 |
0,110708 |
|
-0,60843 |
0,126575 |
0,110708 |
|
-0,69967 |
[m] |
[m] |
d [m] |
[m] |
0,114766 |
0,102025 |
0,023 |
-0,71183 |
0,116227 |
0,103173 |
|
-0,71382 |
0,116954 |
0,102982 |
|
-0,66950 |
0,116591 |
0,103364 |
|
-0,70838 |
0,115132 |
0,103364 |
|
-0,78624 |
Obliczam przedział, w którym znajduje się ogniskowa soczewki z prawdopodobieństwem 68,3%:
Wartość średnia ![]()
= -0,60307m , a odchylenie standardowe ![]()
=0,061556m.
Wartość średnia ![]()
= -0,71795m , a odchylenie standardowe ![]()
=0,0423m.
Po wymnożeniu przez współczynnik Studenta-Fishera, (który dla n=5 pomiarów wynosi 1,2),
![]()
=0,0738672m oraz ![]()
=0,05076m
Ogniskowa wynosi:
![]()
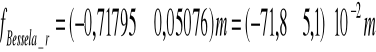
Z prawdopodobieństwem 99,7% ogniskowa soczewki znajduje się w przedziale:
![]()
=0,184668m, po wymnożeniu przez współczynnik studenta-Fishera ![]()
=0,2216016m
![]()
=0,1269m, po wymnożeniu przez współczynnik studenta-Fishera ![]()
=0,15228m
Ogniskowa wynosi:
![]()
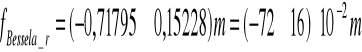
SOCZEWKA A+6
p [m] |
o [m] |
l [m] |
e [m] |
[m] |
[m] |
[m] |
[m] |
0,454 |
0,536 |
0,99 |
0,215 |
0,00476 |
0,245802 |
0,000370 |
0,235827 |
0,449 |
0,541 |
|
0,219 |
0,004671 |
0,245363 |
0,000373 |
0,235389 |
0,450 |
0,540 |
|
0,217 |
0,004689 |
0,245455 |
0,000372 |
0,235609 |
0,465 |
0,525 |
|
0,201 |
0,004957 |
0,246591 |
0,000362 |
0,237298 |
0,452 |
0,538 |
|
0,215 |
0,004724 |
0,245632 |
0,000370 |
0,235827 |
0,463 |
0,527 |
|
0,203 |
0,004921 |
0,246466 |
0,000363 |
0,237094 |
0,458 |
0,532 |
|
0,202 |
0,004831 |
0,246117 |
0,000362 |
0,237196 |
Obliczam przedział, w którym znajduje się ogniskowa soczewki z prawdopodobieństwem 68,3%:
Wartość średnia ![]()
=0,245918m , a odchylenie standardowe ![]()
=0,000485m.
Wartość średnia ![]()
=0,23632m , a odchylenie standardowe ![]()
=0,000834775m.
![]()
Po wymnożeniu przez współczynnik Studenta-Fishera, (który dla n=7 pomiarów wynosi 1,1),
![]()
=0,00053354m oraz ![]()
=0,0009182525m.
Ogniskowa wynosi:
![]()
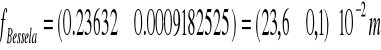
Z prawdopodobieństwem 99,7% ogniskowa soczewki znajduje się w przedziale:
![]()
=0,01455m, po wymnożeniu przez współczynnik studenta-Fishera ![]()
=0,0016005m
![]()
=0,002504325m, po wymnożeniu przez współczynnik studenta-Fishera ![]()
=0,0027547575m
Ogniskowa wynosi:
![]()
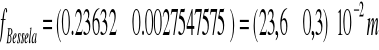
SOCZEWKA 6
[m] |
[m] |
d [m] |
[m] |
0,245802 |
0,107718 |
0,023 |
-0,15081 |
0,245363 |
0,110708 |
|
-0,15982 |
0,245455 |
0,109964 |
|
-0,15754 |
0,246591 |
0,110708 |
|
-0,15917 |
0,245632 |
0,110708 |
|
-0,15967 |
[m] |
[m] |
d [m] |
[m] |
0,235827 |
0,102025 |
0,023 |
-0,13928 |
0,235389 |
0,103173 |
|
-0,14273 |
0,235609 |
0,102982 |
|
-0,14209 |
0,237298 |
0,103364 |
|
-0,14239 |
0,235827 |
0,103364 |
|
-0,14307 |
Obliczam przedział, w którym znajduje się ogniskowa soczewki z prawdopodobieństwem 68,3%:
Wartość średnia ![]()
= -0,1574m , a odchylenie standardowe ![]()
=0,003796m.
Wartość średnia ![]()
= -0,14191m , a odchylenie standardowe ![]()
=0,001516m.
Po wymnożeniu przez współczynnik Studenta-Fishera, (który dla n=5 pomiarów wynosi 1,2),
![]()
=0,0045552m oraz ![]()
=0,0018192m.
Ogniskowa wynosi:
![]()
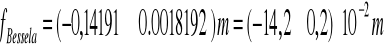
Z prawdopodobieństwem 99,7% ogniskowa soczewki znajduje się w przedziale:
![]()
=0,013656m, po wymnożeniu przez współczynnik studenta-Fishera ![]()
=0,0163872m
![]()
=0,005476m, po wymnożeniu przez współczynnik studenta-Fishera ![]()
=0,00654912m
Ogniskowa wynosi:
![]()
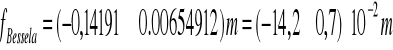
Różnice w wartościach ogniskowych wyznaczonych ze wzoru soczewkowego i metodą Bessela dla soczewek: C, A, 6 są niewielkie, natomiast dla soczewki 4 różnica jest znaczna.
Różnice te wynikaja z ograniczonej dokładności oka ludzkiego ( problem jednoznacznego określenia ostrości obrazu ).
Błędy pomiarowe popełniane przy stosowaniu metody Bessela są w większości przypadków mniejsze od błędów wynikających ze stosowania metody wzoru soczewkowego. Metoda Bessela jest więc dokładniejsza.
9