Wykład 12
Przybliżenie jednoelektrodowe.
Każde ciało składa się z ogromnej ilości jąder i elektronów. Miarą ilości atomów w makroskopowym obiekcie jest liczba Avogadra (N=6.02217 *1023) . Liczba elektronów jest na ogół jeszcze większa.
Dla potrzeb tego wykładu załóżmy , że jądra kryształu lub innego ciała pozostają nieruchome. Wówczas układ opisany być może przez funkcję falową , zależną od położeń wszystkich elektronów ![]()
. r1 , r2
..... rN są wektorami opisujacymi położenia poszczególnych elektronów.
Energie stacjonarne układu można otrzymać rozwiązując równanie Schrödingera
![]()
(I-1)
gdzie hamiltonian H wyraża się następująco
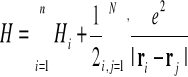
(I-2)
gdzie
![]()
(I-3)
We wzorze tym 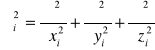
a ![]()
jest energią potencjalną i-tego elektronu. Wskaźnik prim przy sumie we wzorze (I-2) oznacza , ze trzeba pominąć przy sumowaniu wyrazy j=i .
Oczywiście nie znamy ścisłych rozwiązań równania (I-1). Nawet w przypadku kilku elektronów (dwóch) . Stosuje się więc jak zwykle w mechanice kwantowej metody przybliżone.
Omówiona zostanie metoda Hartree' ego - Focka. Podstawowym założeniem tej metody jest zastąpienie w hamiltonianie H potencjalnej energii wzajemnego oddziaływania elektronów polem efektywnym Uef, w którym wszystkie elektrony poruszają się niezależnie. Pole to opisuje uśrednione działanie wszystkich pozostałych elektronów na dany elektron. Przy takim założeniu hamiltonian układu jest równy sumie hamiltonianów zależnych od współrzędnych jednego elektronu.
![]()
(I-4)
gdzie
![]()
(I-5)
Łatwo wykazać, że rozwiązaniem równania (I-1) z takim hamiltonianem jest funkcja w postaci iloczynu :
![]()
![]()
(I-6)
gdzie wskaźnik przy funkcji ni zespół liczb kwantowych charakteryzujących dany elektron. W ogólności wskaźnik ten uwzględnia również spin elektronu. Funkcje falowe ![]()
są rozwiązaniem równań
![]()
(I-7)
gdzie energia ![]()
jest energia i-tego elektronu. Całkowita energia układu jest równa
![]()
(I-8)
Podstawiając hamiltonian (I-4) i funkcję falową (I-6) do równania Schrödingera (I-1) otrzymamy
![]()
(I-9)
Ponieważ hamiltonian ![]()
działa tylko na funkcję falową i-tego elektronu ![]()
zgodnie z równaniem (I-7) równanie (I-9) daje się przekształca się jak następuje
![]()
( I-10)
Dzieląc obustronnie równanie (I-10) przez ![]()
otrzymuje się równanie (I-8) , czego właśnie należało dowieść .
Rozważmy przypadek dwóch elektronów (N=2) . Wówczas funkcja falowa dane będzie następująco ![]()
(I-11) .
Odpowiedni hamiltonian będzie równy
![]()
(I-12)
Zauważmy , że jeśli funkcja ( I-11) jest funkcją własną hamiltonianu (I-12) to funkcja ![]()
(I-13)
jest również funkcją własną tego samego hamiltonianu. Tzn. spełnione są równania
![]()
(I-14)
i
![]()
(I-15)
Funkcja ![]()
różni się od funkcji (I-11) tym, że elektrony zostały zamienione miejscami. Wydaje się oczywiste , że przy zamianie elektronów miejscami nie powinna się zmienić całkowita energia układu. Właściwości przestrzeni Hilberta ( jest to przestrzeń funkcyjna , której elementami są funkcje będące rozwiązaniami odpowiedniego równania Schrödingera , jeśli funkcje (I-11) i (I-13) są funkcjami własnymi hamiltonianu (I-12) to dowolna ich kombinacja liniowa również jest funkcją własną tego hamiltonianu.
Ciekawy jest szczególny przypadek gdy obie funkcje są opisane tymi samymi liczbami kwantowymi , tzn. gdy ![]()
. Jeśli uwzględniono tu spin to wówczas oba elektrony zajmują ten sam stan kwantowy. Ponieważ elektrony są fermionami , zgodnie z zakazem Pauliego taka sytuacja jest niemożliwa. Aby zakaz Pauliego był spełniony automatycznie spośród wszystkich kombinacji liniowych funkcji (I-11) i ( I-12) wybieramy funkcje w postaci
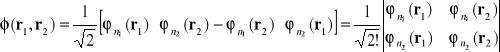
(I-16)
Zauważamy, że jeśli![]()
, wówczas funkcja (I-16) jest równa zeru. Nie istniej układu dwóch elektronów gdy oba scharakteryzowane są przez ten sam zestaw liczb kwantowych. Jeśli mamy do czynienia z większą liczbą elektronów wybieramy funkcję w postaci wyznacznika :
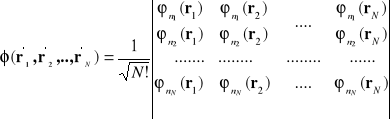
(I-17)
Zauważmy, że funkcja (I-17) jest równa zero gdy dowolne dwa elektrony byłyby scharakteryzowane przez ten sam zespół liczb kwantowych. ![]()
, dla dowolnego ![]()
powoduje , że wyznacznik posiada dwa równe wiersze . Taki wyznacznik jest równy zeru. Wybór wieloelektrodowej funkcji falowej w postaci wyznacznika automatycznie powoduje , ze układ wieloelektrodowy spełniać będzie zakaz Pauliego.
Powróćmy do przypadku dwu elektronów. Spróbujmy podać sposób obliczanie efektywnego potencjału , w którym poruszają się pojedyncze elektrony. Energia układu dwóch elektronów może być obliczona jako
![]()
(I-18)
Przedstawmy hamiltonian w postaci (I-2) uwzględniając potencjał oddziaływania pomiędzy dwoma elektronami. Dla dwóch elektronów hamiltonian będzie miał postać
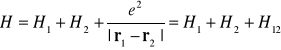
(I-19)
Podstawiając funkcję falową ze wzoru (I-16) , oraz wykorzystując następujące relacje ortogonalności
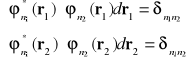
(I-20)
otrzymamy
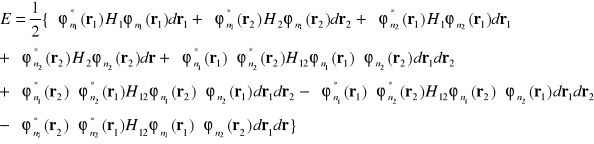
(I-21)
Zauważając, że
![]()
(I-22)
![]()
(I-23)
i
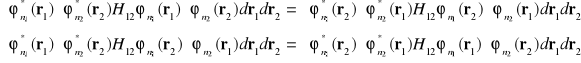
(i-24)
równanie (I-21) może być przekształcone do postaci
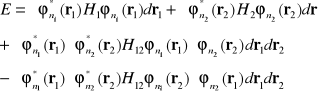
(I-25)
lub po podstawieniu hamiltonian 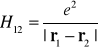
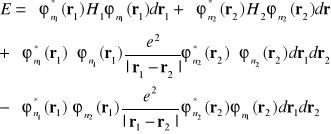
(I-26)![]()
W równaniu (I-26) dwie pierwsze całki odpowiadają energiom elektronów z wewnętrznym potencjale, trzecia całka reprezentuje elektrostatyczne odpychanie się elektronów![]()
i ![]()
są przestrzennymi gęstościami ładunków pierwszego i drugiego elektronu. Czwarta , ujemna całka reprezentuje energię wymiany. Oddziaływanie wymiany nie ma odpowiednika w elektrostatyce klasycznej . Można je interpretować jako oddziaływanie kulombowskie pomiędzy zespolonymi ładunkami opisanymi przez gęstości ładunków ![]()
i ![]()
.
Równanie (I-26) może być łatwo uogólnione na przypadek gdy mamy więcej niż dwa elektrony . Dla N elektronów mamy :
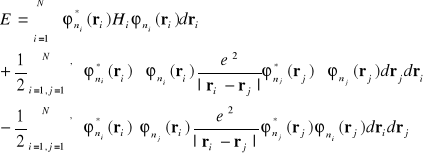
(i-27)
Podobnie jak poprzednio prim przy sumach oznacza , że nie bierze się pod uwagę składników przy i=j.
Wróćmy do problemu znajdowania efektywnego potencjału Uef . Można go znaleźć używając metody wariacyjnej . Rozważmy równanie (I-27) i zbadajmy jak zmienia się energia E jeśli funkcje ![]()
zmienią się o ![]()
. Formalnie zmienia się o wartość ![]()
. Zakładając, że energia E jest "dobrą wartością własną", całka (I-27) musi mieć wartość minimalną. Warunek na minimum powoduje, że ![]()
musi się równać zeru.
Otrzymamy
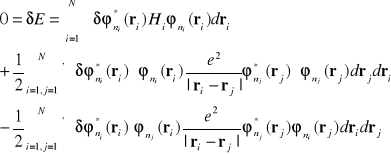
( I-28)
lub
![]()
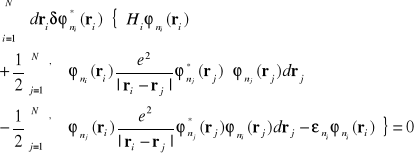
(I-29)
Ostatni składnik w nawiasie we wzorze (I-29) pojawił się ponieważ dla dowolnej wariancji ( zmiany) funkcji ![]()
możemy założyć, że ![]()
dla dowolnego i i j. Ponieważ wariancje funkcji są dowolne zerowanie się sumy wymaga zerowania się wszystkich współczynników przy![]()
. W ten sposób otrzymujemy dla każdego i następujące równanie :
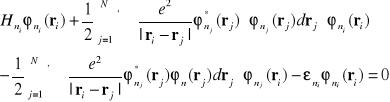
(I-30)
Równanie (I-30 ) można przedstawić w następujący sposób
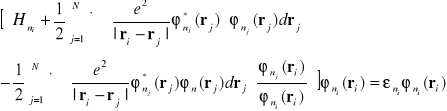
(I-31)
Równanie (I-31) jest równaniem Schrödingera dla i tego elektronu, który porusza się w potencjale efektywnym
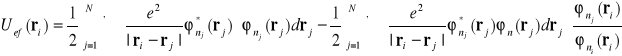
(I-32)
W praktyce energie i funkcje własne układu wieloelektrodowego liczy się w sposób iteracyjny.
Na początku wybiera się początkowe funkcje w postaci wyznaczników (I-17) , następnie oblicza się efektywne potencjały korzystając ze wzoru (I-32) . Potencjały te wstawia się do równań (I-31) i rozwiązując te równania otrzymuje się energie własne ![]()
i odpowiadające im funkcje własne ![]()
w pierwszej iteracji. Tak otrzymane funkcje falowe wstawia się do równania (I-32) i otrzymuje się nowe potencjały efektywne , które z kolei używa się do obliczenia energii i funkcji w drugiej iteracji. Procedurę taką powtarza się dopóty aż różnice energii w kolejnych iteracjach będą znikome. Jeśli właściwie wybierze się warunki początkowe ( czyli wyznacznikowe funkcje własne) wystarczy kilka iteracji aby otrzymać wystarczająco zbieżne rozwiązania.
Metoda iteracyjna , która tu przedstawiono nazywa się często metodą pola samouzgodnionego lub metodą Hartree - Focka.
7
Wyszukiwarka
Podobne podstrony:
Fizyka 0 wyklad organizacyjny Informatyka Wrzesien 30 2012
Fizyka wykład dajzeta 20 02 2011
Zal-lab-BP-zaoczne, politechnika lubelska, budownictwo, 3 rok, semestr 5, fizyka budowli, wykład
kolokwium 14 01 10, polibuda, 3 semestr, fizyka i inżynieria materiałowa (kolokwia, sprawozdania, w
test-B, politechnika lubelska, budownictwo, 3 rok, semestr 5, fizyka budowli, wykład
temp krytyczna, TRANSPORT PWR, STUDIA, SEMESTR II, FIZYKA, fizyka-wyklad, zagadnienia opracowane, za
zestaw1 -wyklad, POLIBUDA, Fizyka (semestr 1)
Fizyka budowli wykład I Żelaz
Program wykładu Fizyka II
SiS strona tytulowa spr, Prz inf 2013, I Semestr Informatyka, Fizyka, Wykłady-Fizyka, Sygnały i Syst
fiza, BUDOWNICTWO PŁ, Semestr I, fizyka wykład
test-d(1), politechnika lubelska, budownictwo, 3 rok, semestr 5, fizyka budowli, wykład
Tytuł, fizyka, wyklady
Fizyka górotworu wykład 2
fizyka budowli kolo z wykladow opracowane 11
Fizyka Matematyczna Wykłady
Fizyka 0 wyklad organizacyjny I Nieznany
więcej podobnych podstron