POLITECHNIKA ŚLĄSKA
Wydział Górnictwa i Geologii
Fizyka.
Zajęcia laboratoryjne.
Wyznaczanie energii maksymalnej promieni β metodą absorpcyjną.
Gliwice 2007r.
gr. sekcja
WSTĘP TEORETYCZNY.
Fizyka jądrowa to dział fizyki zajmujący się jądrami atomów. Jądra składają się z protonów i neutronów, powiązanych siłami jądrowymi. Są to siły krótkiego zasięgu w porównaniu, np. z siłami elektromagnetycznymi, posiadające własność wysycania. Oznacza ona, że nukleon (proton lub neutron) oddziaływanie z każdym kolejnym nukleonem jest coraz słabsze, co sprawia, że oddziałuje on głównie z najbliższymi nukleonami. Jednym z przejawów własności wysycania jest fakt, że energia wiązania - tj. energia potrzebna na rozdzielenie jądra na nukleony - nie jest proporcjonalna do liczby nukleonów w jądrze.
Promieniowanie jądrowe jest to emisja cząstek, lub promieniowania elektromagnetycznego (promieniowanie gamma) przez jądra atomów. Promieniowanie zachodzi podczas, albo po przemianie promieniotwórczej, oraz w wyniku przejścia wzbudzonego jądra do stanu o niższej energii. Rodzaj wysyłanego promieniowania i jego energia zależy od rodzaju przemiany jądrowej. Najbardziej znane rodzaje promieniowania to: promieniowanie alfa, promieniowanie beta i promieniowanie gamma.
Czas połowicznego rozpadu (zaniku) to czas, w ciągu którego liczba nietrwałych jąder atomowych pierwiastka (promieniotwórczego), a zatem i aktywność promieniotwórcza, zmniejsza się o połowę. Jest to wielkość wynikająca z prawa rozpadu naturalnego.
Prawo rozpadu naturalnego to zależność określająca szybkość ubywania pierwotnej masy substancji zbudowanej z jednego rodzaju cząstek, która ulega naturalnemu, spontanicznemu rozpadowi. Prawo to głosi, że jeśli prawdopodobieństwo rozpadu cząstek tworzących substancję jest dla każdej nich jednakowe i niezależne, oraz nie zmienia się w czasie trwania procesu rozpadu, to ubytek masy substancji w niewielkim odcinku czasu można wyrazić wzorem:
dm = -λmdt
Po scałkowaniu:
![]()
gdzie:
m - masa próbki ulegającej rozpadowi,
λ - stała rozpadu charakterystyczna dla danego izotopu lub substancji,
t - czas,
m0 - masa początkowa w momencie t=0,
m(t) - masa w czasie t.
We wzorze na prawo rozpadu zamiast stałej rozpadu λ używana jest wielkość ![]()
zwana średnim czasem życia. Czas po którym w stanie początkowym pozostaje połowa masy próbki (![]()
) nazywa się czasem połowicznego rozpadu (![]()
).
Zależność masy od czasu dla różnych stałych rozpadu.
Przemiany jądrowe uwalniają cząsteczki o bardzo dużej energii zwane promieniowaniem jądrowym. Najczęściej występującymi rodzajami promieniowania są: alfa (jądra helu), beta (elektrony) i gamma (wysokoenergetyczne fotony).
promieniowanie alfa - to rodzaj promieniowania jonizującego cechującego się małą przenikalnością. Promieniowanie alfa jest to strumień jąder helu.
![]()
promieniowanie beta (promieniowanie β) - jeden z rodzajów promieniowania jonizującego wysyłanego przez promieniotwórcze jądra atomowe podczas przemiany jądrowej.
Promieniowanie beta powstaje podczas rozpadu beta. Jest strumieniem elektronów, lub pozytonów poruszających się z prędkością zbliżoną do prędkości światła. Promieniowanie beta jest silnie pochłaniane przez materię, przez którą przechodzi. Promieniowanie to jest zatrzymywane już przez miedzianą blachę.
Przemiana ta może występować w jednym z trzech wariantów:
rozpad negatonowy (z powstaniem elektronu i antyneutrina)
![]()
rozpad pozytonowy (z powstaniem pozytonu i neutrina)
![]()
wychwyt elektronu
![]()
Emisja promieniowania beta. W rogu: pojedynczy rozpad beta.
promieniowanie gamma - to wysokoenergetyczna forma promieniowania elektromagnetycznego. Za promieniowanie gamma uznaje się promieniowanie o energii kwantu większej od 10 keV, co odpowiada częstotliwości większej od 2,42 EHz, a długości fali mniejszej od 124 pm. Zakres ten częściowo pokrywa się z zakresem promieniowania rentgenowskiego. W wielu publikacjach rozróżnienie promieniowania gamma oraz promieniowania X opiera się na ich źródłach, a nie na długości fali. Promieniowanie gamma wytwarzane jest w wyniku przemian jądrowych albo zderzeń jąder lub cząstek subatomowych, a promieniowanie rentgenowskie, w wyniku zderzeń elektronów z atomami. Promieniowanie gamma jest promieniowaniem jonizującym i przenikliwym. Nazwa promieniowania gamma pochodzi od greckiej litery γ.
![]()
Promieniowanie gamma.
Teorię rozpadu opracował włoski fizyk - Enrico Fermi, a szczegółowe rozważania wykraczają poza kurs fizyki klasycznej. Rozpad promieniotwórczy może być realizowany na trzy sposoby:
emisja elektronów:
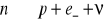
emisja pozytonów:
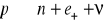
wychwyt elektronów z powłoki trzyjądrowej:

Pierwszy z tych rozpadów może zachodzić dla swobodnego nukleonu, natomiast dwa pozostałe tylko dla nukleonów w jądrach.
Energia emitowanych cząstek β osiąga wartości od zera do pewnej wartości maksymalnej, a widmo energetyczne ma charakter ciągły. Zgodnie z zasadą zachowania energii, część energii powinna przejmować neutralna cząstka o niewielkiej masie. Taką cząstką jest neutrino, a antycząstką - antyneutrino. Cząstki te posiadają spin połówkowy, tak jak elektron (lub pozyton). Energia cząstek β może osiągać wartości od 10 keV do 10 MeV. Największą energię posiadają cząstki β w przypadku, gdy rozpad zachodzi bez udziału neutrino (bądź antyneutrino).
Elektrony mogą być usuwane z wiązki wskutek:
jonizacji
zderzeń sprężystych z elektronami i jądrami
zderzeń niesprężystych i związanego z nimi promieniowania hamowania
Dla pierwiastków lekkich przeważa jonizacja, dla ciężkich - procesy jonizacji i zderzeń z jądrami mają podobny wpływ na proces osłabiania energetycznego wiązki cząstek β.
Proces przejścia elektronów przez absorbującą substancję jest złożony, a zanim jego energia zmaleje do zera, może zderzyć się z wieloma elektronami (lub jądrami). W wiązce cząstek β mamy elektrony, lub pozytony o ciągłym widmie energetycznym. Absorpcję β opisuje następująca funkcja ekspotencjalna:
![]()
gdzie:
x - grubość absorbenta,
μ - liniowy współczynnik pochłaniania,
I - rejestrowane natężenie promieniowania po przejściu przez absorbent.
Ciągłe zwiększanie grubości absorbenta nie doprowadzi do całkowitego wyeliminowania promieniowania β.
Energię maksymalną monoenergetycznych cząstek możemy wyznaczyć z zależności empirycznych. W naszym przypadku analizujemy proces absorpcji cząstek β przez folię aluminiową. Przyjmując, że liczba zliczeń przelicznika w określonym czasie jest proporcjonalna do natężenia wiązki promieni wychodzących przez okienko licznika Geigera-Müllera, można zależność przedstawić na wykresie w skali logarytmicznej.
Licznik Geigera (licznik Geigera-Müllera) jest to urządzenie opracowane przez Hansa Geigera wraz z Walterem Müllerem w 1928 roku, mierzące promieniowanie jonizujące. Ponieważ jonizacja gazów wewnątrz licznika zachodzi nie tylko w wyniku promieniowania alfa, ale także innych rodzajów promieniowania jonizującego (beta i gamma), toteż licznik Geigera zlicza w istocie niemal całkowity poziom czynników jonizujących w otoczeniu.
Zwiększanie grubości absorbenta nie doprowadzi do uzyskania zerowej liczby zliczeń. Nawet podczas nieobecności źródła promieniowania układ licznik - przelicznik zarejestruje pewną liczbę zliczeń, zwaną tłem. Impulsy tła mogą powstać pod wpływem promieniowania kosmicznego, promieniotwórczości substancji zanieczyszczających powietrze, samorzutnymi wyładowaniami licznika i szumem układu zliczającego.
CEL ĆWICZENIA.
Celem ćwiczenia jest wyznaczenie energii maksymalnej promieniowania metodą absorpcyjną.
PRZEBIEG ĆWICZENIA.
Włączamy przelicznik.
Mierzymy tło licznika (pomiar liczby zliczeń w czasie 10 min przy nieobecności preparatu).
Preparat ujmujemy szczypcami i wstawiamy razem z podstawką w wycięcie pierścienia wstawionego uprzednio w szczelinę domku ołowianego. Preparat umieszczamy otworem do góry.
Nastawiamy tryb pomiaru czasu zliczania [s] zadanej liczby impulsów.
Pomiary wykonujemy najpierw bez absorbenta, a następnie z płytkami aluminiowymi dokładanymi na stos na preparat.
OPRACOWANIE WYNIKÓW POMIAROWYCH.
Rysujemy wykres zależności N' = f(d).
Wykreślamy zależność N' = f(d) stosując dla osi N' skalę logarytmiczną. Przedłużamy wykres do przecięcia się z rzędną N' = Nt. Określamy zasięg liniowy promieni β w aluminium.
Obliczamy zasięg masowy promieni β. Na podstawie danych zawartych w poniższej tabeli, rysujemy wykres zależności zasięgu masowego promieni β w aluminium od ich energii maksymalnej.
Emax [keV] |
100 |
150 |
200 |
250 |
300 |
400 |
500 |
800 |
1000 |
Zasięg [mg/cm2] |
13.5 |
26.5 |
42 |
59 |
78 |
120 |
165 |
310 |
420 |
Określamy energię maksymalną promieni stosowanego preparatu 204Tl.
Przeprowadzamy graficzną analizę błędów.
TABELA POMIAROWA.
tło [10 min] = 84, N' = 8,4, lnN' = 2,13
grubość 10 płytek = 0,53 [mm]
Lp. |
Liczba płytek |
Grubość d [mm] |
Impulsy N |
Czas t [s] |
N' [min-1] |
|
lnN' |
|
1. |
- |
- |
1000 |
11 |
5455 |
|
8,60 |
0 |
2. |
1 |
0,053 |
1000 |
17,4 |
3448 |
58,72 |
8,15 |
0,001 |
3. |
2 |
0,106 |
1000 |
22,7 |
2643 |
51,41 |
7,88 |
0,002 |
4. |
3 |
0,159 |
1000 |
31,3 |
1916 |
43,77 |
7,56 |
0,003 |
5. |
4 |
0,212 |
1000 |
38 |
1579 |
39,74 |
7,36 |
0,004 |
6. |
5 |
0,265 |
1000 |
48,4 |
1240 |
35,21 |
7,12 |
0,005 |
7. |
6 |
0,318 |
1000 |
63 |
952 |
30,86 |
6,86 |
0,006 |
8. |
7 |
0,371 |
1000 |
86,6 |
693 |
26,32 |
6,54 |
0,007 |
9. |
8 |
0,424 |
1000 |
114,6 |
524 |
22,88 |
6,26 |
0,008 |
10. |
9 |
0,477 |
1000 |
163,3 |
367 |
19,17 |
5,91 |
0,009 |
11. |
10 |
0,53 |
1000 |
229,4 |
262 |
16,17 |
5,57 |
0,01 |
ANALIZA BŁĘDÓW.
Wykonując pojedynczy pomiar liczby zliczeń przy pomocy przelicznika, można temu pomiarowi przypisać błąd średni, który jest równy pierwiastkowi kwadratowemu z liczby zliczeń N'.
ΔN' = ![]()
Pomiary grubości blaszek wykonano mikrometrem o dokładności 0,01[mm].
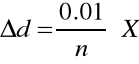
Błąd pomiaru grubości został obliczony z następującego wzoru:
gdzie:
n - liczba wszystkich płytek aluminiowych,
X - numer kolejnej płytki dokładanej na stos.
Przedłużenie prostoliniowego odcinka wykresu zależności ln |N'| do przecięcia z rzędną odpowiadającą logarytmowi tła wyznacza zasięg liniowy promieni w aluminium.
![]()
= 1,18 mm
REGRESJA LINIOWA y = ax + b
Wartości współczynników a, b obliczono programem „Analiza”.
a = (-5,39![]()
0,13)
b = (84,98![]()
0,22)*10-1
r = -0,99
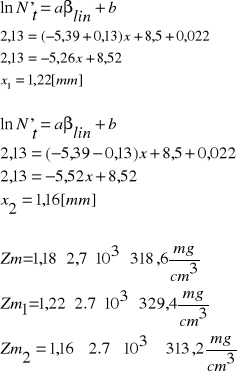
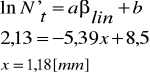
![]()
Znając zasięg masowy Zm możemy odczytać energię maksymalną promieni w aluminium:
Emax=815 ![]()
15 [keV]
WNIOSKI.
Wykonane ćwiczenie wykazało, że pochłanianie energii promieniowania jest zależne od grubości absorbenta, którym w naszym przypadku jest aluminium. Poprzez zwiększanie grubości absorbenta, liczba przenikających cząstek przez absorbent maleje.
Dla cząstek można wyznaczyć tzw. zasięg efektywny R, czyli grubość absorbenta, którą przenika tylko bardzo mała część padających cząstek.
Pobrano z: www.wikipedia.pl
Pobrano z: www.wikipedia.pl
Pobrano z: www.wikipedia.pl
1
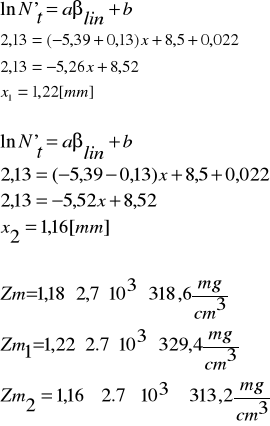
![]()
Wyszukiwarka
Podobne podstrony:
Projekt betonu sekcja 1, GiG sem I - III
Pomiar mocy i energii w ukladach jednofazowych, GiG sem I - III
Analiza widmowa, GiG sem I - III
widmowa, GiG sem I - III
projekt muru oporowego, AGH Kier. GiG rok III Sem. V, ge
Zarys Geomechaniki wykład, AGH Kier. GiG rok III Sem. V, Zarys geomechaniki
I termin 2015 beta wersja, far, III rok IV sem, biologia molekularna, kolokwia 2015 pytania
Promieniowanie Beta, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL,
chemia egzamin odp2, AGH Kier. GiG rok II Sem. III
TT Sem III 14 03
MOJE 3ok, Budownictwo UZ sem. III
Funkcjonowanie klasycznego systemu MRP, Materiały dla ZiP, sem III
Elektrowrzeciono, Studia, Studia sem III, Uczelnia
więcej podobnych podstron